| ИВМ СО РАН | Поиск |
| Отчеты ИВМ СО РАН |
Отчет ИВМ СО РАН за 2012 год
Гранты российских научных фондов
- Гранты РФФИ
- Проект РФФИ №
11–01–00 053 — «Численное моделирование термомеханических процессов в средах с микроструктурой на суперкомпьютерах» - Грант РФФИ №
11–01–00 106-а «Численное моделирование динамических процессов в больших электрических сетях» - Грант РФФИ №
11–01–00 224-а — «Метод траекторий и конечных элементов для решения уравнений Навье-Стокса для вязкого теплопроводного газа» - Грант РФФИ №
11–01–00 283-а — «Структуры и устойчивость течений сопряженных задач тепломассообмена» - Грант РФФИ №
12–05–00 152-а — «Математическое моделирование влияния магнитосферных и ионосферных процессов на атмосферные электрические поля» - Проект РФФИ
12–01–31 069_мол_а «Влияние эффекта Соре на режимы конвективных течений в многокомпонентных смесях» - Грант РФФИ
12–07–31 143_мол_а. Разработка методов и средств концептуального OLAP-моделирования для информационно-аналитической поддержки предупреждения возникновения и смягчения последствий чрезвычайных ситуаций - Грант РФФИ №
12–01–90 820-мол_рф_нр — «Исследование многосеточного метода решения уравнений гидрогазодинамики. Научный проект Андреевой Евгении Михайловны из Южно-Российского регионального центра информатизации Южного федерального университета, г. Ростов-на-Дону в ИВМ СО РАН, г. Красноярск» - Грант РФФИ №
12–01–90 804-мол_рф_нр — «Развитие суперкомпьютерных технологий решения задач динамики деформируемого твердого тела. Научная работа Архипова Ильи Николаевича из Национального исследовательского Томского политехнического университета, г. Томск, в Институте вычислительного моделирования СО РАН, г. Красноярск» - Грант РФФИ №
12–01–90 900-моб_снг_ст — «Научная работа Шерстобитова Антона Вячеславовича из Казахстана, Усть-Каменогорская городская специализированная школа для детей, одарённых в области математики, физики, информатики, г. Усть- Каменогорск, в Институте вычислительного моделирования РАН, г. Красноярск. Геометрия многогранников с паркетными гранями» - Грант РФФИ №
11–04–98 089-р-Сибирь «Оценка и прогноз вклада бореальных лесов Восточной Сибири в глобальный круговорот углерода» - Грант РФФИ №
12–01–09 235_моб_з — «Численное решение динамических задач в блочных средах с тонкими прослойками на суперкомпьютерах с ГПУ для представления на научном мероприятии «Пятая конференция по численному анализу и приложениям» - Грант РФФИ №
12–01–09 236_моб_з — «Параллельная реализация на SMP-узловом кластере метода конечных элементов для задачи эллиптического типа» для представления на научном мероприятии «Пятая конференция по численному анализу и приложениям» - Грант РФФИ №
12–01–91 269-РФГ_з — «Участие в трехстороннем российско-французско-немецком семинаре: «Обобщенный Континуум в качестве моделей для материалов с мультимасштабным эффектом или под мультиполярным воздействием» - Грант РФФИ
12–07–09 254-моб_з — «Метод построения интегральной OLAP-модели на основе анализа формальных понятий» для представления на научном мероприятии «Международная конференция по инженерным, интеллектуальным и основанным на знаниях системам» - Гранты Красноярского краевого фонда поддержки науки и научно-технической деятельности
Гранты РФФИ
Проект РФФИ №
№ гос. регистрации 01201159524
Руководитель: д.ф.-м.н., профессор В. М. Садовский
На основе акустического приближения уравнений динамики структурно неоднородной упругой среды с вращательными степенями свободы частиц микроструктуры материала построена упрощенная математическая модель для описания волновых движений нематического жидкого кристалла под действием слабых механических и температурных возмущений. В пространственном случае модель образуют уравнения поступательного и вращательного движения для векторов линейной и угловой скорости, определяющие уравнения, записанные относительно давления и антисимметричного тензора касательных напряжений, и кинематические уравнения для вектора-директора, задающего пространственную ориентацию частиц — удлиненных молекул жидкого кристалла. Температурные факторы моделируются с помощью связанного уравнения теплопроводности, учитывающего объемное температурное расширение среды, в котором тензор теплопроводности из-за различия в коэффициентах теплопроводности вдоль молекул и в поперечном направлении определяется ориентацией частиц.
Показано, что в случае плоской деформации касательное напряжение в среде удовлетворяет уравнению Клейна-Гордона, описывающему осцилляционный характер вращения частиц. В плоской постановке исследован вопрос о возможности инициирования волн вращательного движения в жидком кристалле, изменяющих его оптические свойства, за счет действия тепловых источников на границе. Показано, что изменение ориентации при слабых тепловых воздействиях может быть связано только с действием касательных напряжений на границе.
Разработан последовательный прототип компьютерной программы для анализа термомеханического поведения жидкокристаллической среды под действием импульсных силовых и температурных возмущений. Выбран приемлемый вариант схемы расщепления уравнения теплопроводности со смешанными производными, входящего в основную систему, по пространственным переменным. Пример, демонстрирующий работу этой схемы, представлен на рис. VI.1.

Рис. VI.1. Изменение температурного поля со временем в зависимости от ориентации молекул жидкого кристалла
Разработаны параллельные программы для систем с GPU, реализующие параллельный алгоритм численного решения системы уравнений для описания нестационарных процессов термоупругой деформации жидкого кристалла.
Основные публикации:
- Sadovskaya O., Sadovskii V.
Mathematical Modeling in Mechanics of Granular Materials. Series: Advanced Structured Materials [Электронный ресурс] / Springer: Heidelberg — New York — Dordrecht — London, 2012. — V. 21. — 390 p. ISSN: 1869–844 1 (electronic). ISBN: 978-3-642–290 53-4 (eBook). Режим доступа: http://link.springer.com/book/10.1007/978-3-642–290 53-4. - Садовский В. М., Садовская О. В., Варыгина М. П.
Комплекс параллельных программ для моделирования упругопластических волн в структурно неоднородных средах // Сб. тр. междунар. науч. конф. «Параллельные вычислительные технологии 2012». — Новосибирск: ИВМиМГ СО РАН, 2012. — С. 662–672 . - Садовский В. М., Садовская О. В.
Об акустическом приближении термомеха-нической модели жидкого кристалла // Физическая мезомеханика (в печати).
(Отдел вычислительной механики деформируемых сред)
| К началу | |
Грант РФФИ №
№ гос. регистрации 01201159527
Руководитель: д.ф.-м.н., профессор Е. А. Новиков
Создана динамическая гибридная модель электрической сети, учитывающая возможные критические ситуации. Построены методы второго и третьего порядков точности для решения гибридных задач и проведены их тестовые испытания на многопроцессорной вычислительной системе кластерной архитектуры. Разработаны новые аддитивные методы решения жестких задач, в которых допускаются различные способы аппроксимации матрицы Якоби.
Основные публикации:
- Новиков Е. А., Шорников Ю. В.
Компьютерное моделирование жестких гибридных систем. — Новосибирск: НГТУ, 2012. — 450 с. - Novikov E. A.
The variable structure algorithm based on L-stable and explicit methods // Russian Journal of Numerical Analysis and Mathematical Modeling. — 2012. — V. 27. — № 3. — P. 243–259 . - Новиков Е. А.
Алгоритм интегрирования третьего порядка с замораживанием матрицы Якоби для жестких задач // Системы управления и информационные технологии. — 2012. — № 3 (49). — С. 24-28. - Новиков Е. А.
Численный метод третьего порядка для решения аддитивных неавтономных жестких задач // Вычислительные методы и программирование. — 2012. — Т. 13. — С. 479–490 . - Новиков Е. А., Кнауб Л. В., Новиков А. Е.
Численное моделирование орегонатора трехстадийными явными методами // Информатика и системы управления. — 2012. — № 3 (33). — С. 59-68.
(Отдел вычислительной математики)
| К началу | |
Грант РФФИ №
№ гос. регистрации 01201159525
Руководитель: член-корреспондент РАН В. В. Шайдуров
Блок 1. Численное решение нестациогарных уравнений Навье-Стокса для вязкого теплопроводного газа (В. В. Шайдуров, Г. И. Щепановкая, М. В. Якубович).
Система двумерных нестационарных уравнений Навье-Стокса для вязкого теплопроводного газа включает четыре квазилинейных дифференциальных уравнений в частных производных, вытекающих из законов сохранения массы, количества движения и внутренней энергии газа. Для аппроксимации суммы первых производных каждого уравнения системы (субстанциональных производных) используется метод траекторий, который заключается в аппроксимации этой суммы с помощью разностной производной назад по времени вдоль траектории движения частицы. Оставшиеся дифференциальные слагаемые в уравнениях аппроксимируются методом конечных элементов с линейными, квадратичными или кубическими элементами. Здесь новизна состоит в аппроксимации кинетической и внутренней энергии в гильбертовых пространствах, для чего в уравнении внутренней энергии проводится замена искомой функции. В результате на дискретном уровне достигается закон сохранения полной энергии, обеспечивающий также устойчивость построенных вычислительных алгоритмов. Отметим, что дискретные системы метода конечных элементов после аппроксимации субстанциональной производной разностным методом обладают существенно лучшими вычислительными свойствами и поэтому их сборка и численное решение более экономичны с вычислительной точки зрения. Построенные алгоритмы в совокупности являются более эффективными по сравнению с известными в настоящее время алгоритмами для этой задачи. В процессе вычислительного эксперимента изучены различные задания условий на границе расчётной области в методе конечных элементов, что становится актуальным для решения реальных задач.
Проведена серия тестовых расчетов для трех вариантов граничных условий, вычислен сеточный аналог нормы погрешности компоненты скорости $\textit{u}$ в пространстве $L_{2} $ (рис. VI.2 — VI.3). В первом варианте для всех искомых функций на границе расчетной области ставятся условия Дирихле (на рис. VI.2 — VI.3 кривые 1, 2). Во втором варианте для скорости и внутренней энергии на границе выхода потока ставятся условия Неймана (кривые 3, 4), третий вариант — случай исчезающей вязкости в области около выходной границы (кривые 5, 6, 7, 8 соответствуют различным значениям динамического коэффициента вязкости). Вариант с исчезающей вязкостью для небольшого числа Рейнольдса $\textit{Re} = 104$ оказался предпочтительнее по сравнению с условиями Неймана.
Замена искомых функций в уравнениях неразрывности и внутренней энергии обеспечивает повышение точности приближенного решения, и приводит к меньшей абсолютной погрешности в нормах $L_{2}$ и $L_{\infty}$. Применение комбинации метода траекторий и метода конечных элементов не требует согласования триангуляций на соседних временных слоях, что значительно облегчает динамическое разрежение или сгущение триангуляций по времени для оптимизации вычислительной работы или улучшения аппроксимации в пограничных слоях и ударных волнах. Для решения систем алгебраических уравнений используется многосеточный метод с внешними итерациями по нелинейности. Совокупность метода траекторий и метода конечных элементов позволяет построить экономичный алгоритм с вычислительной точки зрения. Численная реализация построенных алгоритмов осуществлена для высокопроизводительных вычислительных кластеров.
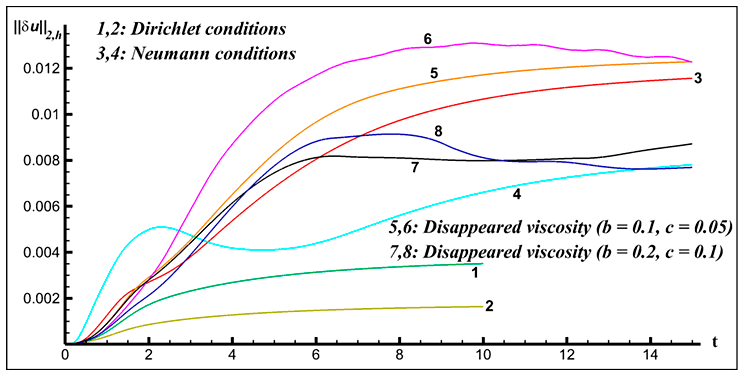
Рис. VI.2. $\textit{L}_{2}$ норма погрешности функции скорости $\textit{u}$ при числе Рейнольдса $\textit{Re} = 2\times 10^{3}$
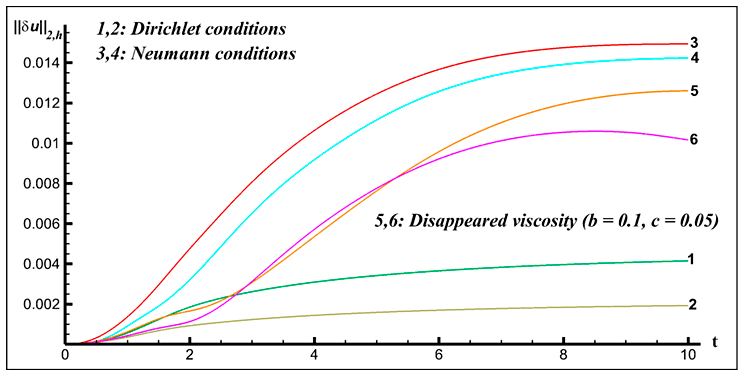
Рис. VI.3. $\textit{L}_{2}$ норма погрешности функции скорости $\textit{u}$ при числе Рейнольдса $\textit{Re} = 10^{4}$
Блок 2. Метод траекторий для уравнения неразрывности (А. В. Вяткин, В. В. Шайдуров).
Для решения системы уравнений Навье-Стокса разработан модифицированный метод траекторий, аппроксимирующий уравнение неразрывности. В основе метода лежит доказанное тождество о точном равенстве масс, расположенных на соседних временных слоях и заключенных в объемах (площадях) с границами, которые определяются траекториями движения частиц назад по времени. Теоретически доказано и экспериментально подтверждено, что предложенная численная схема имеет первый порядок точности и является сходящейся в дискретном аналоге нормы пространства $\textit{L}_{1}$ при фиксированном отношении шага по времени к шагу по пространству. Тестовые расчеты и сравнение со схемой набегающего потока (upwind scheme) показали, что максимальная величина абсолютной погрешности для указанных двух схем отличается не значительно. Кроме того, ввиду использования траекторий, метод позволяет пренебречь условием устойчивости Куранта-Фридрихса-Леви и сформулировать иное ограничение на шаг по времени. При проведении численных экспериментов это позволило для ряда тестовых задач увеличить шаг по времени до величины в 10 раз превышающей максимальное допустимое значение, соответствующее условию Куранта-Фридрихса-Леви. Для повышения порядка сходимости до четвертого использован метод экстраполяции Ричардсона. Вместе с тем, главными преимуществами разработанного метода являются:
- выполнение закона сохранения массы при переходе на очередной временной слой;
- отсутствие требования о согласовании триангуляций вычислительной области на соседних временных слоях, что значительно облегчает динамическое разрежение или сгущение сетки.
Кроме того, процесс распараллеливания и обобщения предложенного алгоритма на трехмерный случай не представляет собой принципиальной сложности.
Блок 3. Реализация алгоритмов для различных технологий программирования (MPI, OpenMP и CUDA), а также их комбинаций на конкретных вычислительных системах. Определение лимитирующих факторов параллелизации созданных алгоритмов и пути их оптимизации (Е. Д. Карепова, Е. В. Дементьева).
Для задачи Дирихле для уравнения в частных производных второго порядка эллиптического типа в многоугольной области построен метод конечных элементов (МКЭ) с линейными треугольными конечными элементами на неструктурированной согласованной триангуляции.
Для описанного класса задач проведен анализ эффективности параллельной реализации для гибридной архитектуры SMP-узлового кластера.
Сборка невязки при реализации метода конечных элементов на согласованной неструктурированной триангуляции для рассматриваемого класса задач может производиться поэлементно (традиционный способ, реализующий наиболее выгодное распределение памяти) или по узлам сетки (приводит к необходимости создания в памяти структур переменного размера, увеличивает время работы с памятью). При последовательной реализации алгоритма и при использовании технологии MPI наиболее эффективным считается поэлементная сборка.
Показано, что для распараллеливания в рамках технологии OpenMP для вычислительных систем с общей памятью алгоритм сборки невязки в МКЭ существенно влияет на эффективность параллельной реализации. Например, на синхронизацию нитей внутри основного цикла при сборке невязки по элементам тратится до 40% времени выполнения цикла. При поузловой сборке синхронизация нитей в основном цикле не требуется, однако из-за неэффективного хранения данных о триангуляции существенно увеличивается время, затрачиваемое на обращение к памяти.
Идет отладка последовательной программы с поузловой и поэлементной сборкой невязки с оптимизацией алгоритма для реализации на графических процессорах c применением технологии CUDA.
Основные публикации:
- Schepanovskaya G. I., Shaidurov V. V., Yakubovich M. V.
Numerical modelling of supersonic flows in channel // Russ. J. Numer. Anal. Math. Model. — 2012. — V. 27 (6). — P. 501–516 . - Вяткин А. В., Шайдуров В. В.
Численная схема, основанная на методе траекторий, для уравнения неразрывности // Материалы XVI Междунар. науч. конф. «Решетневские чтения». — Красноярск: СибГАУ, 2012. — Ч. 2. — C. 531–532 .
(Отдел вычислительной математики)
| К началу | |
Грант РФФИ №
№ гос. регистрации 01201159523
Руководитель: д.ф.-м.н., профессор В. К. Андреев
1. Найдены симметрии двумерных уравнений движения бинарной смеси, учитывающих зависимость коэффициентов переноса от температуры и концентрации. Решена задача групповой классификации относительно коэффициентов вязкости, температуропроводности, диффузии и термодиффузии. Выделены специализации этих функций в зависимости от вида функции, отвечающей за силу плавучести. Построены алгебры Ли операторов, допускаемых уравнениями, в зависимости от перечисленных произвольных элементов. Следует отметить, что при решении задачи учитывалось, что все коэффициенты переноса не обращаются в ноль, коэффициенты температуропроводности и диффузии не совпадают, а сила плавучести может отсутствовать, тогда исходные уравнения описывают движение жидкости в невесомости. Построено точное решение уравнений термодиффузии, инвариантное относительно операторов, полученных в результате исследования групповых свойств данных уравнений. Решение представляет собой обобщение течения Пуазейля, возникающего между двумя параллельными плоскостями при наличии постоянного градиента давления. Вид решения существенно зависит от коэффициентов вязкости, температуропроводности, диффузии и термодиффузии жидкости.
2. Доказано неравенство Фридрихса, когда общая область состоит из объединения шара и шарового слоя и учитываются все граничные условия, включая и поверхность раздела. На его основе получены априорные оценки сопряжённой начально-краевой задачи для параболических уравнений с заданными источниками тепла, которые являются функциями только радиальной координаты и времени. Из доказанных априорных оценок выводится не только единственность решения рассматриваемой задачи, но и его асимптотическое поведение при больших временах. Приводится решение этой же задачи методом преобразования Лапласа. В образах по Лапласу решение находится в виде квадратур. Доказано, что если источники тепла имеют предел при $t\to \infty$, то и решение выходит на стационарный режим. Здесь же решена и обратная задача по восстановлению источника тепла в шаре, если дополнительно на внешней поверхности шарового слоя задан поток тепла. При выводе априорных оценок основная трудность была в получении оценок поля температур в шаре. Принцип максимума здесь применять нельзя, так как коэффициенты имеют особенность в начале координат. Необходимо воспользоваться известной формулой решения с двойными интегралами, где температура на границе шара совпадает с температурой слоя, для которой априорная оценка уже получена. Решающую роль здесь играет различное представление функции Грина для шара.
3. При хранении жидких сред в цилиндрических сосудах между ними возникает граница раздела. Среды находятся в равновесии, а затем под действием нагрева одного из оснований в системе может возникнуть движение. Эта ситуация и анализируется при некоторых ограничениях, именно, жидкости находятся в состоянии невесомости и справедлив принцип смены устойчивости — комплексный декремент равен нулю. В этом случае удалось найти аналитические выражения для нейтральных чисел Марангони. Доказано, что с ростом радиуса цилиндра эти числа стремятся к известным числам Марангони для контактирующих жидкостей в бесконечных слоях. Это лишний раз подтверждает правильность полученных формул. Кроме того, решена задача о возникновении конвекции Марангони в однослойном конечном цилиндре со свободной поверхностью.
4. Исследована задача о совместном однонаправленном движении трёх вязких теплопроводных жидкостей в слоях. Источником движения является термокапиллярный эффект на двух поверхностях раздела, который вызывается постоянным градиентом давления, приложенным вдоль твёрдых стенок. Найдено стационарное движение системы, состоящее из сопряжённых течений Куэтта в слоях. Доказано, что всегда нестационарное движение с ростом времени по экспоненциальному закону выходит на этот режим.
5. Проведено исследование термокапиллярных течений и их устойчивости в бесконечном жидком цилиндре, окруженном коаксиальным слоем газа с заданным расходом. Слой газа ограничен твёрдой цилиндрической поверхностью, которая может перемещаться в вертикальном направлении. В слоях задан постоянный осевой градиент температуры. Найдено точное решение уравнений движения, описывающее стационарное течение в данной двухфазной системе. Изучены возможные режимы течений и их устойчивость в линейном приближении. Рассмотрены случаи недеформируемой и деформируемой границы раздела.
6. В рамках модели микроконвекции рассмотрена задача о конвективном течении в вертикальном слое при линейном распределении температуры поперек слоя. Изучена структура спектра возмущений и границы устойчивости. Показано, что при выбранных значениях параметров задачи наиболее опасной является плоская монотонная мода. В этом случае неустойчивость связана с развитием гидродинамических возмущений на границе встречных потоков.
7. Рассмотрено совместное движение бинарной смеси и вязкой теплопроводной жидкости с общей поверхностью раздела. Источником движения является термоконцентрационный эффект на поверхности раздела жидких сред. Найдено стационарное движение системы. Показано, что в слоях реализуется течение типа Куэтта. С ростом времени скорость, распределение температуры и концентрации выходят на стационарный режим.
Основные публикации:
- Андреев В. К., Резникова И. А.
Оценки решений сопряжённой тепловой задачи в шаровой области // J. of Siberian Federal University. Mathematics and Physics. (в печати). - Андреев В. К.
О корректности начально-краевой задачи, описывающей волны на воде // Материалы LXV науч. конф. «Герценовские чтения — 2012». — СПб, 2012. — С. 25-30. - Stepanova I. V.
Group classification for equations of thermodiffusion in binary mixture // Communication in Nonlinear Science and Numerical. (в печати). - Лемешкова Е. Н.
Стационарное течение трех жидкостей в плоском слое под действием термокапиллярных сил и перепада давления // J. of Siberian Federal University. Mathematics and Physics. — 2012. — № 5 (1). — P. 91-96. - Андреев В. К., Лемешкова Е. Н.
Термокапиллярное движение трёх вязких жидкостей в плоском слое // ПММ.(в печати). - Андреев В. К., Бекежанова В. Б.
Об одном решении уравнений свободной конвекции при наличии объемных источников тепла // ПММ. (в печати). - Рыжков И. И., Андреев В. К.
О термокапиллярной неустойчивости жидкого цилиндра, обдуваемого потоком газа // J. of Siberian Federal University: Mathematics and Physics. (в печати). - Лемешкова Е. Н.
О совместном движении трёх вязких неизотермических жидкостей в плоском слое // Вычислительные технологии. (в печати).
(Отдел дифференциальных уравнений механики)
| К началу | |
Грант РФФИ №
№ гос. регистрации 01201260709
Руководитель: д.ф.-м.н., профессор В. В. Денисенко
Построена математическая модель электрических полей в ионосфере и в верхней атмосфере, которые генерируются грозовыми облаками. Показано, что эти поля практически не могут быть измерены спутниковыми средствами, поскольку они малы по сравнению с полями, обычно существующими в среднеширотной ионосфере.
Основные публикации:
- Denisenko V. V., Hausleitner W., Stangl G., Biernat H. K.
Mathematical simulation of quasi-stationary electric fields penetration through the Earth's atmosphere // Book of Abst. of the 9-th Int. Conf. «Problems of Geocosmos». St.-Petersburg, 2012. — P. 117–118 . - Erkaev N. V., Semenov V. S., Biernat H. K.
Current sheet oscillations in the magnetic filament approach // Physics of plasmas, 2012. — V.19, Iss. 6. — P. 062905.
(Отдел вычислительной математики)
| К началу | |
Проект РФФИ
№ гос. регистрации 01201275321
Руководитель: к.ф.м.н. И. И. Рыжков
При экспериментальном измерении коэффициентов диффузии и термодиффузии часто используется конфигурация плоского слоя, подогреваемого снизу или сверху. Основным требованием к эксперименту является чисто диффузионный тепломассообмен в исследуемой смеси. Однако неоднородности температуры и концентрации в поле силы тяжести могут привести к возникновению конвективного движения. В связи с этим является актуальной задача об устойчивости механического равновесия в плоском слое смеси при различных режимах подогрева.
Рассматривается бесконечный плоский слой многокомпонентной смеси, подогреваемый снизу (или сверху) в поле силы тяжести. В основном состоянии движение отсутствует, при этом постоянный градиент температуры в слое приводит к возникновению постоянных градиентов концентрации компонентов благодаря эффекту Соре.
В пределе длинных волн критическое число Рэлея для монотонной неустойчивости дается формулой
\[{\rm Ra}_{m} =720\Pr \left(\sum _{j=1}^{n-1}\psi _{j} {\rm Sc}_{j} \right)^{-1},~~~~~~~(VI.1) \]
а для колебательной неустойчивости получается выражение
\[{\rm Ra}_{o} =720\Pr \left(\sum _{j=1}^{n-1}\frac{\psi _{j} {\rm Sc}_{j}^{-1} }{\omega ^{2} +{\rm Sc}_{j}^{-2} } \right)^{-1},~~~~~~~(VI.2)\]
где частота $\omega $ удовлетворяет уравнению
\[\sum _{j=1}^{n-1}\frac{\psi _{j} }{\omega ^{2} +{\rm Sc}_{j}^{-2} } =0.~~~~~~~(VI.3)\]
Здесь $\Pr $ — число Прандтля, ${\rm Sc}_{j} $ — число Шмидта компонента $j$, $\psi _{j} $ — отношение разделения компонента $j$, характеризующее эффект Соре, $n$ — число компонентов смеси. Уравнение (VI.3) не имеет решения, если отношения разделения компонентов $\psi _{j} $ имеют одинаковые знаки, а также в случаях, когда все числа Шмидта одинаковы или смесь является бинарной $(n=2)$. Таким образом, длинноволновая колебательная неустойчивость может существовать только в смесях с тремя и большим числом компонентов, которые имеют различные диффузионные и термодиффузионные свойства (часть компонентов концентрируется в более нагретых областях, другая часть — в более холодных).
Для произвольных значений волнового числа задача об устойчивости решалась численно. Использовались методы Галеркина и пошагового интегрирования с ортогонализацией на основе метода Рунге-Кутты-Мерсона 5-го порядка точности.
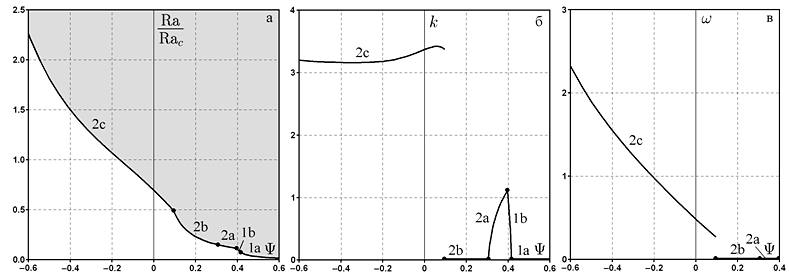
Рис. VI.4. Зависимость критических параметров неустойчивости тройной смеси от суммарного отношения разделения $\Psi$. Число Рэлея (а), волновое число (б), круговая частота (в). Параметры смеси: $\psi _{1} =0.4,{\rm \; }\Pr =10,{\rm \; Sc}_{{\rm 1}} {\rm =100,\; Sc}_{{\rm 2}} =1000$
Для описания тройных смесей удобно использовать пространство параметров $(\Psi {\rm, \; }\psi _{{\rm 1}}, s,{\rm Sc}_{2} )$, где $\Psi {\rm \; =}\psi _{{\rm 1}} +\psi _{2} $ есть суммарное отношение разделения, $s={\rm Sc}_{1} /{\rm Sc}_{2} $ — отношение чисел Шмидта. Без ограничения общности можно считать $0 \lt s \le 1$. Как показывают расчеты, если $s=1$ (оба компонента имеют одинаковые диффузионные времена), то смесь ведет себя подобно бинарной смеси с отношением разделения $\Psi {\rm \; =}\psi _{{\rm 1}} +\psi _{2} $. В случае $0 \lt s \lt 1$ критические параметры неустойчивости зависят не только от суммарного отношения разделения $\Psi $, но и от отношения разделения $\psi _{{\rm 1}} $. На рис. VI.4 показана зависимость критических параметров от $\Psi $ для тройной смеси с параметрами $\psi _{1} =0.4,{\rm \; }\Pr =10,{\rm \; Sc}_{{\rm 1}} {\rm =100,\; Sc}_{{\rm 2}} =1000{\rm \; \; (}s{\rm \; =\; 0.1)}$ при подогреве сверху ($Ra \gt 0$). Число Рэлея нормировано на значение $Ra_{c} =1707.76$, которое является критическим для слоя однокомпонентной среды. Кривые 1a, 1b соответствуют монотонной неустойчивости, кривые 2a, 2b, 2c — колебательной неустойчивости. В отличие от бинарной смеси, здесь появляется длинноволновая колебательная неустойчивость (кривая 2b). Критические параметры длинноволновой неустойчивости определяются по формулам (1) — (3).
Основные публикации:
- Рыжков И. И.
Длинноволновая неустойчивость плоского слоя многокомпонентной смеси с эффектом Соре // МЖГ. — М., 2012 (в печати). - Ryzhkov I. I.
Soret separation in a two-phase ternary system and its stability // Abstr. of 10-th Int. meeting on thermal diffusion. — Brussels, 2012. — P. 85. - Ryzhkov I. I.
Термодиффузия в смесях: уравнения, симметрии, решения и их устойчивость // Монография. 2012 (подана на издательский конкурс РФФИ и представлена заявка на включение в план изданий СО РАН).
(Отдел дифференциальных уравнений механики)
| К началу | |
Грант РФФИ
№ гос. регистрации 01201274703
Руководитель: к.т.н. А. В. Коробко
Для оперативного анализа обстановки и формирования управленческих решений выполнено проектирование и информационное наполнение централизованного хранилища данных мониторинга чрезвычайных ситуаций. Разработана оригинальная структура хранилища данных, включающая слой длительного хранения, слой аналитических объектов и слой предзагрузочной обработки данных. Для комплексного анализа мониторинговых данных разработаны OLAP-модели по обстановкам. На основе OLAP-моделей разработаны ключевые показатели и критерии оценивания обстановки для индикации степени риска возникновения чрезвычайных ситуаций. Предложен подход к формированию иерархической системы аналитических индикаторов для комплексного оценивания обстановки.
Основные публикации:
- Пенькова Т. Г., Коробко А. В.
Аналитическая поддержка принятия решений на основе концептуальной OLAP-модели предметной области // Материалы XI Всерос. науч.-техн. конф. «Теоретические и прикладные вопросы современных информационных технологий» (ТиПВСИТ'2012). — Улан-Удэ, 2012. — С.393–399 . - Пенькова Т. Г., Коробко А. В.
Построение концептуальной OLAP-модели предметной области для оперативной аналитической обработки данных // Материалы всерос. конф. «VI Всесибирский конгресс женщин-математиков», 2012. — С. 166–171 . - Коробко А. В., Пенькова Т. Г.
Поддержка адаптивного манипулирования объектами анализа на основе концептуальной OLAP-модели // Материалы XV Всерос. семинара «Моделирование неравновесных систем», 2012. — С. 89-93.
(Отдел прикладной информатики)
| К началу | |
Грант РФФИ №
Руководитель: член-корреспондент РАН В. В. Шайдуров, к.ф.-м.н. Е. М. Андреева
Основной целью проекта являлось создание относительно простого и эффективного с вычислительной точки зрения численного алгоритма решения уравнений Навье-Стокса для вязкой несжимаемой жидкости с использованием многосеточной технологии. Основные задачи проекта:
- исследование способов аппроксимации системы дифференциальных уравнений;
- исследование и выбор эффективных методов грубо-сеточной коррекции многосеточного метода;
- теоретическое и численное исследование сглаживающих процедур для эффективного решения уравнений Навье-Стокса многосеточным методом.
Численное решение — важнейший этап математического моделирования, который состоит из двух основных частей: дискретизации и метода решения системы алгебраических уравнений, полученной в результате дискретизации исходных уравнений. В ходе выполнения проекта был предложен некоторый подход для решения уравнений Навье-Стокса в задачах гидродинамики.
Рассматривалась система из трех двумерных нестационарных уравнений Навье-Стокса для определения двух компонент скорости и давления течения вязкой несжимаемой жидкости. Для аппроксимации совокупности производной по времени и инерциальных первых производных по пространству предложено использовать метод траекторий, который заключается в аппроксимации всей этой совокупности с помощью одной разностной производной назад по времени вдоль траекторий движения частиц. Дискретизация по пространству остальных слагаемых осуществляется методом конечных элементов. Такой комбинированный способ аппроксимации предложен впервые О. Пиронно в 1980-м году и все чаще используется в расчетах. В методе конечных элементов применяется комбинация простых конечных элементов: билинейных для скоростей и постоянных для давления. Эта комбинация обеспечивает устойчивость вычисления давления с дополнительным применением численной фильтрации.
В результате дискретизации на каждом слое по времени получается система линейных алгебраических уравнений с симметричной матрицей, имеющей знакопеременный спектр. Для решения полученной системы уравнений эффективным является применение многосеточного метода. Его основное преимущество состоит в оптимальной оценке числа арифметических операций O(N), пропорциональной числу неизвестных N, для достижения заданной точности. Основными алгоритмическими составляющими многосеточного метода являются сглаживающая процедура и грубо-сеточная коррекция. Алгоритм многосеточного метода позволяет значительно повысить эффективность базового итерационного метода, комбинируя обычный итерационный процесс с приемом, называемым грубо-сеточной коррекцией последовательным использованием решений на более грубых сетках.
Основные публикации:
- Муратова Г. В., Андреева Е. М.
Многосеточный метод решения задач в анизотропной среде // Тез. докл. VI Всерос. конф. «Актуальные проблемы прикладной математики и механики». — Екатеринбург: УрО РАН, 2012. — С. 54-55. - Shaydurov V. V., Andreeva E. M., Muratova G. V.
Mixed finite element method for solving the Navier-Stokes equations with multigrid method // Theses of the First China-Russia Conference on Numerical Algebra with Applications in Radiative Hydrodynamics. — Beijing, China, 2012. — P. 17.
(Отдел вычислительной математики)
| К началу | |
Грант РФФИ №
Руководитель: д.ф.-м.н., профессор В. М. Садовский, И. Н. Архипов
На основе серии расчетов распространения волн напряжений и деформаций в блочных средах проведены верификация и тестирование программных комплексов для численного решения двумерных и пространственных задач динамики упругопластических и сыпучих сред 2Dyn_Granular и 3Dyn_Granular на вычислительных кластерах высокой производительности. Усовершенствован модуль построения пространственных расчетных сеток в программном комплексе «РАНЕТ-3», предназначенном для моделирования контактного взаимодействия ударников с многослойными преградами.
Основные публикации:
- Архипов И. Н.
Компьютерное моделирование процессов ударного взаимодействия стального стержня с многослойной экранной защитой // Материалы XVI Междунар. науч. конф. «Решетневские чтения». — Красноярск: СибГАУ, 2012. — Ч. 2. — С. 470–471 .
(Отдел вычислительной механики деформируемых сред)
| К началу | |
Грант РФФИ №
Руководитель: д.ф.-м.н., профессор А. В. Тимофеенко
Подготовлено к опубликованию доказательство следующей теоремы.
Теорема. На проективной плоскости дан четырехугольник $\textit{ABCD}$. Пусть $\textit{P}$ — пересечение $\textit{AD}$ и $\textit{BC}$, $\textit{Q}$ — переченеие $\textit{AB}$ и $\textit{CD}$, $\textit{R}$ — произвольная точка плоскости, отличная от вышеуказанных и $\textit{A'}$ — произвольная точка прямой $\textit{RA}$, отличная от $\textit{R}$ и $\textit{A}$. Если $\textit{B'}$ — пересечение $\textit{A'Q}$ и $\textit{BR}$, $\textit{D'}$ — пересечение $\textit{A'P}$ и $\textit{DR}$, то в шестиугольник $\textit{A'B'BCDD'}$ можно вписать кривую второго порядка.
Отлажена технология построения орбиты многогранника при действии на него группой движений с последующим объединением многогранников орбиты и удалением граней, которые принадлежат сразу двум многогранникам. Построены полуоднородные тела, у которых каждая грань (не обязательно выпуклый) правильный многоугольник и существуют описанная и касающаяся всех ребер сферы. В частности, создана алгебраическая и компьютерная модель полуоднородного 104-гранника, порождённого усечённым кубом. Найдены возможные типы трёхгранных вершин выпуклых многогранников с правильными и паркетными гранями. Во время стажировки А.В. Шерстобитов был постоянным участником спецкурса А.В. Тимофеенко о многомерных многогранниках и группах их симметрий и активно работал на научном семинаре «Группы и правильногранники». Получил опыт создания алгебраических моделей многогранников и их компьютерных реализаций в системе компьютерной алгебры Maple.
Основные публикации:
- Шерстобитов А. В.
Полуоднородные многогранники // Вестник КГПУ. — 2012. — № 2 (20). — С. 158–163 .
(Отдел дифференциальных уравнений механики)
| К началу | |
Грант РФФИ №
Руководитель: академик РАН А. Г. Дегерменджи,
Ответственный исполнитель от ИВМ: д.ф.-м.н. В. М. Белолипецкий
Проведен нейросетевой анализ динамики глобальной температуры за последнее столетие как функции парниковых газов, солнечной и вулканической активностей, индексов активности океанических циркуляций. В рамках малоразмерных моделей продемонстрирована возможность триггерных переключений между состояниями системы «биосфера-климат» в результате возмущения глобального баланса углерода, например, массовыми вырубками леса или лесопосадками.
С помощью нейросетевого анализа предложено объяснение сложной динамики глобальной температуры, включающей потепление начала XX в. (когда влияние парниковых газов было малым), выход на плато в последние 10 лет (хотя концентрации парниковых газов продолжали расти). При этом ведущим фактором потепления второй половины XX в. выступают антропогенные парниковые газы.
Основные публикации:
- Bartsev S. I., Degermendzhi A. G., Belolipetsky P. V.
Carbon cycle modeling and principle of the worst scenario. In: Jordan F., Jorgensen S. E. (Eds) // Models of the ecological hierarchy: from molecules to the ecosphere. Elsevier B. V., 2012. — Р. 447–458 . - Белолипецкий П. В., Барцев С. И.
Нейросетевой анализ влияния различных факторов на климат 20 века // Тез. докл. всерос. конф. «Солнечная активность и природа глобальных и региональных климатических изменений». — Иркутск: Институт солнечно-земной физики СО РАН, 2012. — С. 4-5.
(Отдел вычислительных моделей в гидрофизике)
| К началу | |
Грант РФФИ №
Руководитель: М. П. Варыгина
Пятая международная конференция по численному анализу и приложениям (Fifth conference on Numerical Analysis and Applications, NAA'12) проходила в с. Лозенец (Болгария).
Направления работы конференции: численная аппроксимация и вычислительная геометрия, численная линейная алгебра и численное решение трансцендентных уравнений, численные методы для дифференциальных уравнений, численная стохастика, численное моделирование, высокопроизводительные вычисления.
Были заслушаны пленарные и секционные доклады, рассмотрены стендовые доклады. Всего в конференции приняли участие 97 специалистов из научных центров, исследовательских институтов, университетов, представляющих 24 страны.
На конференции сделаны доклады:
- М. П. Варыгина «Numerical Solution of Dynamic Problems in Block Media with Thin Interlayers on Supercomputers with GPUs»;
Основные публикации:
- Varygina M.
Numerical Solution of Dynamic Problems in Block Media with Thin Interlayers on Supercomputers with GPUs // Fifth Con. on Numerical Analysis and Applications (NAA'12), 15 — 20 June 2012. Abstr. Lozenetz, Bulgaria, 2012. — P. 52. - Varygina M.
Numerical Solution of Dynamic Problems in Block Media with Thin Interlayers on Supercomputers with GPUs // Lecture Notes in Computer Science. — Springer: Berlin Heidelberg — New York, 2013 (в печати).
(Вычислительной механики деформируемых сред)
| К началу | |
Грант РФФИ №
Руководитель: Е. В. Дементьева
Пятая международная конференция по численному анализу и приложениям (Fifth conference on Numerical Analysis and Applications, NAA'12) проходила в с. Лозенец (Болгария).
Направления работы конференции: численная аппроксимация и вычислительная геометрия, численная линейная алгебра и численное решение трансцендентных уравнений, численные методы для дифференциальных уравнений, численная стохастика, численное моделирование, высокопроизводительные вычисления.
Были заслушаны пленарные и секционные доклады, рассмотрены стендовые доклады. Всего в конференции приняли участие 97 специалистов из научных центров, исследовательских институтов, университетов, представляющих 24 страны.
На конференции сделаны доклады:
- Дементьева Е. В., Карепова Е. Д. «The numerical solution of the inverse problem for the Shallow Water Models»;
- Карепова Е. Д., Дементьева Е. В. «SMP-nodes cluster Parallel Implementation of Finite Element Method for Elliptic-Type Problem».
Основные публикации:
- Karepova E., Dementyeva E.
The numerical solution of the inverse problem for shallow water models // 5-th Conf. on Numerical Analisis and Applications. — Bulgaria, Rousse: University of Rousse Publ., 2012. — P.23-24. - Dementyeva E., Karepova E.
SMP parallel realization of finite element method for elliptic-type problem // 5-th Conf. on Numerical Analisis and Applications. — Bulgaria, Rousse: University of Rousse Publ., 2012. — P.10. - Karepova E., Dementyeva E.
The numerical solution of the inverse problem for shallow water models // Lecture Notes in Computer Science. — Springer: Berlin Heidelberg — New York, 2013 (в печати).
(Отделы Вычислительной математики)
| К началу | |
Грант РФФИ №
Руководитель: М. П. Варыгина
В трехстороннем семинаре «Обобщенный Континуум в качестве моделей для материалов с мультимасштабным эффектом или под мультиполярным воздействием» приняли участие ведущие ученые в этой области из Германии, Франции и России.
В ходе семинара особое внимание было уделено последним исследованиям в следующих областях: новые обобщенные модели; исследования микроструктуры материалов; многопрофильные нагрузки; возможности для выявления определяющих уравнений; старые проблемы с неправильными или неудовлетворительными решениями, основанными на классических предположениях.
На конференции сделан доклад М. П. Варыгина «High-performance computations in the problems of dynamics of the Cosserat continuum».
Основные публикации:
- Sadovskii V., Sadovskaya O., Varygina M.
High-performance computations in the problems of dynamics of the Cosserat continuum // Second Trilateral Scientific Seminar «Generalized Continua as Models for Materials with Multi-scale Effects or under Multi-field Actions». Book of abstracts. Eds: H. Altenbach, S. Forest, A. M. Krivtsov. Wittenberg, Germany, 2012. — P. 36.
(Отдел вычислительной механики деформируемых сред)
| К началу | |
Грант РФФИ
Руководитель: к.т.н. Т. Г. Пенькова
Международная конференция по интеллектуальным системам (International Conference on Knowledge-Based and Intelligent information and Engineering Systems, KES-2012) проходила в Испании, в городе Сан-Себастьян с 10 по 12 сентября 2012 года. В рамках работы конференции обсуждались актуальные проблемы в области экспертных систем, гибридных интеллектуальных систем, обнаружения, представления и управления знаниями, интеллектуального анализа и управления.
В рамках работы секции «Экспертные системы и системы, основанные на знаниях» (Knowledge Based and Expert Systems) представлен доклад «Метод построения интегральной OLAP-модели на основе анализа формальных понятий» (название на английском языке «Method of Constructing the Integral OLAP-model based on Formal Concept Analysis»).
По итогам конференции опубликована статья Penkova T., Korobko A. Method of constructing the integral OLAP-model based on formal concept analysis в журнале Frontiers in Artificial Intelligence and Applications издания IOS Press.
Грант использован на компенсацию расходов на командировку (организационный взнос и транспортные расходы), связанных с участием в работе международной конференции.
Основные публикации:
- Penkova T. Korobko A.
Method of constructing the integral OLAP-model based on formal concept analysis // Frontiers in Artificial Intelligence and Applications. — IOS Press, 2012. — V. 243. — Р. 219–227 .
(Отдел прикладной информатики)
| К началу | |