| ИВМ СО РАН | Поиск |
| Отчеты ИВМ СО РАН |
Отчет ИВМ СО РАН за 2013 год
Программы фундаментальных исследований сибирского отделения РАН
- III.22. Механика жидкости, газа и плазмы, многофазных и неидеальных сред, механика горения, детонации и взрыва
- IV.35. Когнитивные системы и технологии, нейроинформатика и биоинформатика, системный анализ, искусственный интеллект, системы распознавания образов, принятие решений при многих критериях
- IV.36. Системы автоматизации, CALS-технологии, математические модели и методы исследования сложных управляющих систем и процессов
- IV.38. Проблемы создания глобальных и интегрированных информационно-телекоммуникационных систем и сетей. Развитие технологий и стандартов GRID
III.22. Механика жидкости, газа и плазмы, многофазных и неидеальных сред, механика горения, детонации и взрыва
Программа III.22.4. Математический анализ моделей динамики неоднородных сред
Координатор программы: член-корреспондент РАН П. И. Плотников
Проект III.22.4.3. Математическое и численное моделирование сопряжённых задач механики неоднородных сред№ гос. регистрации 01201356263
Научный руководитель проекта: д.ф.-м.н., профессор В. К. Андреев
Блок 1.
1.1. Рассматривалась система уравнений движения жидкой пленки по наклонной плоскости (Кузнецов В. В., 2009)
\[p=-h_{xx} +Ah-Cx,\, \, \, \, \, \, h_{t} +\left(M\frac{q(x,t)h^{2} }{2} -\frac{p_{x} h^{3} }{3} \right)_{x} =0,~~~~~(III.1)\]
где $\textit{h}(\textit{x},\textit{t})$ — толщина пленки; $\textit{p}(\textit{x},\textit{t})$ — давление; $\textit{q}(\textit{x},\textit{t})=\textit{$\theta{}_{x}$}(\textit{x},\textit{t}), \textit{$\theta(x,t)$}$ — температура на поверхности пленки; $\textit{A}$, $\textit{C}$, $\textit{M}$ — физические постоянные. Для системы (III.1) решалась задача групповой классификации по отношению функции $\textit{q}(\textit{x},\textit{t})$ и постоянных $\textit{A}$, $\textit{C}$, $\textit{M}$. Оказалось, что основная группа Ли системы (III.1) состоит только из тождественных преобразований. Перечислены все возможные расширения группы Ли; например, при $\textit{M} \neq 0$ допускается оператор $X=n\partial _{x} +m\partial _{t}, n, m = const,$ а $\textit{q}=\textit{q}(\textit{mx-nt})$, и может быть построено решение в виде бегущей волны. Для $\textit{q} = \textit{$q{}_{0}$}(\textit{t})x$ имеется решение вида
\[h(t)=2h_{0} \left[2-h_{0} M\int _{0}^{t}q_{0} (\tau )\, d\tau \right]^{-1},\]
которое может разрушаться за конечное время, m = const — начальная толщина пленки. (В. К. Андреев).
1.2. Стационарные однонаправленные термодиффузионные течения в горизонтальном слое при нелинейной силе плавучести описываются уравнениями
\[\begin{array}{l} {\rho _{0}^{-1} p_{x} =-gF(\theta ,c),\, \, \, \, \, \, \, \rho _{0}^{-1} p_{z} =\nu w_{xx} ,} \ {w\theta _{z} =\chi (\theta _{xx} +\theta _{zz} ),\, \, \, \, \, \, \, wc_{z} =D(c_{xx} +c_{zz} )+D^{\theta } (\theta _{xx} +\theta _{zz} ).} \end{array}~~~~~(III.2)\]
Ось $\textit{z}$ направлена горизонтально, ось $\textit{x}$ перпендикулярна оси $\textit{z}$, сила плавучести $\textit{F}(\textit{$\theta$},\textit{c})$ действует в направлении, противоположном оси $\textit{x}$, вертикальная компонента скорости считается функцией координаты $\textit{x}$. Течение индуцируется действием силы плавучести и продольного градиента температуры.
Условия совместности первых двух уравнений системы (III.2) позволили получить условие для функции $\textit{F}(\textit{$\theta$,c})$, при котором возможно существование решения системы:
\[\theta _{z}^{2} F_{\theta \theta } +2\theta _{z} c_{z} F_{\theta c} +c_{z}^{2} F_{cc} +\theta _{zz} F_{\theta } +c_{zz} F_{c} =0.~~~~~(III.3)\]
Анализ уравнения (III.3) приводит к трем основным случаям: температура и концентрация являются только функциями одной пространственной переменной; концентрация зависит от двух пространственных переменных, температура — от одной; температура существенно зависит от двух пространственных переменных. Во втором и третьем случаях получены новые точные решения системы (III.2), нелинейно зависящие от координат, что является существенным отличием полученных решений от решений, рассчитанных по модели Обербека-Буссинеска с линейной зависимостью функции $\textit{F}(\textit{$\theta$,c})$ от ее аргументов. С помощью анализа переопределенной системы ОДУ показано, что коэффициенты при производных функции $\textit{F}(\textit{$\theta$,c})$ в равенстве (III.3) не могут быть постоянными. Отдельно исследован случай механического равновесия системы, при котором в некоторых частных случаях решение системы (III.2) сводится к решению уравнений Эйконала. Изучен случай чисто тепловой конвекции, построено точное решение при логарифмической зависимости силы плавучести от температуры. Поставлены и решены две краевые задачи, описывающие течение между двумя твердыми стенками однослойной и двухслойной жидкости с плоской недеформируемой границей раздела. В качестве граничных условий заданы условия прилипания, распределение температуры на твердых стенках и поток жидкости через поперечное сечение слоя. Для двухслойной жидкости на поверхности раздела $\textit{x} = 0$ задаются равенства скоростей, температур, потоков тепла, динамическое условие.
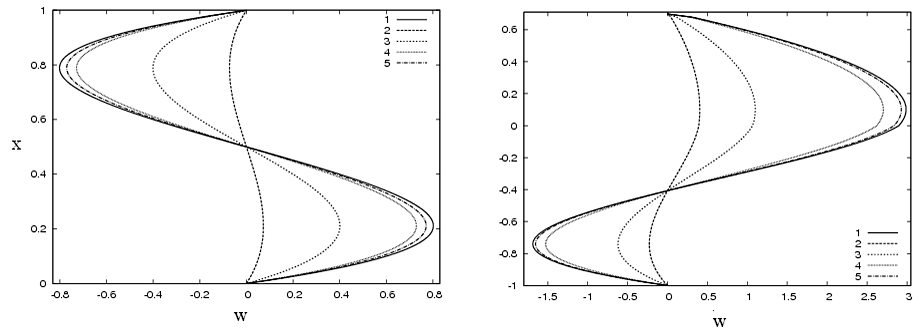
Рис. III.1. Профили скорости однослойного (слева) и двухслойного (справа) течения жидкости между твердыми стенками
Сравнение полученного профиля скорости с профилем, рассчитанным по классической модели Обербека — Буссинеска, показано на рис. III.1, где кривая 1 соответствует скорости при линейной зависимости силы плавучести от температуры и концентрации, а кривые 2-5 — логарифмической зависимости с уменьшающимся от кривой 2 к кривой 5 параметром $\textit{$\delta$}$, отвечающим за распределение продольного градиента температуры. Очевидно, что для произвольного параметра $\textit{$\delta$}$ имеется существенное отличие скорости от решения, рассчитанного по модели Обербека — Буссинеска (В. К. Андреев, И. В. Степанова).
1.3. Изучались дифференциальные алгебры формальных и сходящихся степенных рядов, зависящих от произвольного конечного числа переменных. Введено понятие пассивного семейства образующих дифференциального идеала этих алгебр. Оно является дальнейшим развитием понятия базиса Гребнера. Доказана теорема, позволяющая проверять пассивность семейства образующих и гарантирующая существование и единственность точечного решения бесконечной системы уравнений в данной алгебре. Доказательство основного утверждения принципиально отличается от классического доказательства для дифференциальных уравнений.
Дано определение обобщенных функционально-инвариантных решений класса N для уравнения распространения звука в двумерной стационарной неоднородной среде. Изучены условия на плотность и скорость звука, при которых существуют обобщенные функционально-инвариантные решения класса 2. Предложен метод построения точных обобщенных функционально-инвариантных решений.
Рассмотрена полуэмпирическая модель осесимметричной турбулентной струи, содержащая дифференциальные уравнения переноса нормальных рейнольдсовых напряжений. Найдена алгебра Ли операторов, допускаемых рассматриваемой моделью. С помощью операторов преобразований растяжения получена редукция модели к системе обыкновенных дифференциальных уравнений, которая, в свою очередь, решалась численно. Был использован модифицированный метод стрельбы и асимптотическое разложение решения в окрестности особой точки. Проведено сопоставление полученных результатов с имеющимися экспериментальными данными и результатами расчетов по полной модели (О. В. Капцов, Ю. В. Шанько, А. В. Шмидт).
Блок 2.
2.1. Исследовано совместное однонаправленное движений трёх вязких теплопроводных несмешивающихся жидкостей, которое возникает под действием эффектов Марангони на поверхности раздела и перепадов давления в слоях. Найдено точное стационарное решение, а решение для нестационарного режима получено методом преобразования Лапласа. Доказано, что всегда решение выходит на стационарный режим, если градиент давления в одной из жидкостей является таковым (В. К. Андреев, Е. Н. Лемешкова).
2.2. Разработана программа расчета неодномерных течений с целью изучения устойчивости сопряженных конвективных потоков. В качестве основных уравнений для всех программ расчета использовались уравнения конвекции в приближении Обербека — Буссинеска или уравнения микроконвекции.
Процедура получения основного течения.
Для анализа решений задач гидродинамики, которые не могут быть получены аналитически, и последующей их обработки разработана программа, использующая численный метод, основанный на идее расщепления по физическим процессам. Основными являются уравнения конвекции в приближении Обербека — Буссинеска, записанные в физических переменных. Наибольшую трудность представляет решение уравнений Навье — Стокса. Поэтому расщепление по физическим процессам (конвекция и диффузия) основано на методе слабой аппроксимации для этих уравнений и использует свойство аддитивности этих процессов при малых шагах по времени.
Для двумерных течений на этапе конвекции вводится вспомогательная функция скорости V, и уравнения реализуются на смещенных сетках. На этапе диффузии в качестве новых искомых функций вводятся вихрь и функция тока, а в качестве истинной принимается «диффузионная» скорость. При реализации этапа диффузии удается исключить вычисление давления и разделить задачи для счета вихря и функции тока, если использовать метод прогонки с параметрами.
Расчет двумерных течений в закритичной области параметров.
Для исследования режимов течений, вызванных конвективной неустойчивостью, осуществляется нелинейное моделирование. Основная система переписывается в терминах «вихрь-функция тока» и интегрируется с некоторыми начальными данными с помощью конечно-разностного метода. Уравнения и граничные условия аппроксимируются на равномерной сетке со вторым порядком точности по пространственным координатам. При этом для решения нелинейных уравнений используется явная схема, для которой шаги интегрирования выбираются из условий устойчивости и сходимости. Уравнение Пуассона (для функции тока) решается с использованием итерационной процедуры Либмана на каждом шаге по времени.
Для использования данного метода расчета предварительно исследуется линейная устойчивость основного решения исходной системы и определяются критические значения параметров. Возникающая при этом спектральная задача решается методом ортогонализации или методом Галеркина. Для получения необходимого начального приближения комплексного декремента может быть использована численная процедура поиска, не требующая предварительных оценок. Затем, используя описанный выше численный алгоритм, решается основная система в закритичной области значений параметров.
Расчет возможных вторичных режимов.
На основе данных, полученных в результате линейного анализа устойчивости решений исходной системы, определяются области и типы возникающих неустойчивостей. В случае монотонной потери устойчивости в системе развиваются стационарные вторичные режимы. Особенности вторичных движений могут быть исследованы только путем анализа полных нелинейных уравнений для возмущений основного течения. Для решения данной задачи используется метод малого параметра. Искомые функции (компоненты вектора скорости, давления и температуры) представляются в виде разложений по степеням некоторого малого вещественного параметра $\varepsilon$ (амплитуда периодической компоненты):
\[(U,P,T)=\sum _{n=1}^{\infty }\varepsilon ^{n} (U^{(n)} ,P^{(n)} ,T^{(n)} ) ,\, \, \, \, \, \, G=\sum _{n=0}^{\infty }\varepsilon ^{n} G^{(n)} ,\, \, \, \, \, \, \varepsilon =\varepsilon (G)=G-G_{*} .\, \, \, \]
Здесь $G_{*}$ — критическое значение основного параметра подобия (например число Рэлея, Грасгофа, Марангони, Рейнольдса), которое определяется в результате линейного анализа.
После подстановки последних выражений в полную систему уравнений для возмущений требуем выполнения равенств в каждом порядке по $\varepsilon$. В первом порядке однородные уравнения совпадают с уравнениями для нейтральных возмущений основного течения. А в более высоких порядках возникают неоднородные уравнения, решение которых и позволяет определить характеристики возникающих вторичных течений.
При колебательной потере устойчивости могут быть вычислены мгновенные поля скоростей и температур из решения системы, возникающей в первом порядке по $\textit{$\varepsilon$}$. Для этого в области закритичных значений параметров для колебательной неустойчивости используется метод конечных разностей и строится продольно-поперечная схема второго порядка точности по пространственным переменным. В результате реализации в каждый момент времени строятся поля скоростей и температур, позволяющие определить поведение системы (В. Б. Бекежанова).
Все программы реализованы на языке FORTRAN в среде Fortran PowerStation 4.0.
Блок 3.
3.1. Рассмотрена математическая модель бароклинных сейш для трехслойной плотностной стратификации в бассейнах прямоугольной формы. Для расчетов вертикальных распределений температуры и солености воды в озере Шира использовалась одномерная в вертикальном направлении математическая модель [Белолипецкий В. М., Генова С. Н. Численное моделирование годовой динамики вертикальной структуры соленого озера // Вычислительные технологии. — 2008. — Т. 9, № 4. — С. 34-43; Genova S. N., Belolipetskii V. M., Rogozin D. Y., Degermendzhi A. G. A one-dimensional model of vertical stratification of Lake Shira focussed on winter conditions and ice cover // Aquat. Ecol. — 2010. — V. 44. — P. 5
Для оценки влияния внутренних волн на вертикальную структуру стратифицированного водоема рассматривалась следующая упрощенная постановка задачи. Стратифицированный водоем схематизируется трехслойной жидкостью. В верхнем слое воды, прилегающем к свободной поверхности, из-за перемешивания плотность воды равна постоянному значению, в среднем слое, в пикноклине плотность изменяется линейно по глубине, в придонном слое плотность меняется мало.
Волновые процессы в жидкости изучались на основе линеаризованных уравнений гидродинамики. Рассматривалась задача о колебаниях трехслойной жидкости в замкнутом водоеме прямоугольной формы с плоским дном. Были использованы приближения Буссинеска, гидростатики, твердой крышки. Из системы вытекает основное уравнение внутренних волн относительно вертикальной скорости. Предлагается следующий алгоритм для оценки влияния внутренних волн на вертикальную структуру стратифицированного озера.
1. На первом этапе решается одномерная (в вертикальном направлении) задача без учета внутренних волн. Определяется динамика вертикальных распределений температуры, солености и плотности воды.
2. На втором этапе для конкретных суток рассчитанные вертикальные распределения температуры, солености, плотности воды схематизируются трехслойной жидкостью. Затем определяются колебания температуры и солености в пикноклине в течение суток из решения уравнений
\[\frac{\partial \, T}{\partial \, t} +w\, \frac{\partial \, T}{\partial \, z} =0, \, \, \, \, \, \, \frac{\partial \, S}{\partial \, t} +w\, \frac{\partial \, S}{\partial \, z} =0,\]
где вертикальная составляющая вектора скорости определяется по модели бароклинных сейш.
Выполнены расчеты вертикальных распределений температуры, солености и плотности воды в озере Шира по одномерной модели. Одномерная модель без учета внутренних волн позволяет с удовлетворительной точностью определить положения термоклина, халоклина и пикноклина, а также значения температуры и солености в поверхностном и придонном слоях. Колебания температуры и солености воды в пикноклине оцениваются по упрощенной модели внутренних сейш.
В рамках трехмерной модели течения неоднородной жидкости в приближении Буссинеска и гидростатики проведены расчеты для бассейна с батиметрией оз. Шира и начальными данными, характерными для озера Шира в летний период. Численные расчеты проводились при нестационарном ветре, соответствующем реальной ветровой картине на период летних измерений по данным метеостанции в районе озера Шира в 2013 г.
Эффект более интенсивного перемешивания в прибрежной зоне (рис. III.2, точка Т1) подтверждается данными натурных наблюдений на озере Шира в 2013 г. (рис. III.4) (В. М. Белолипецкий, Л. А. Компаниец, С. Н. Генова, П. В. Белолипецкий, Т. В. Якубайлик).
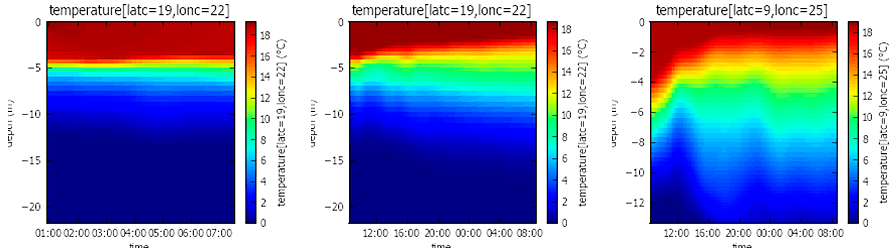
Рис. III.2. Изотермы, полученные в расчетной точке, ближайшей к T3 при постоянном ветре (слева), в ней же после прекращения действия ветра (в центре) и в расчетной точке, ближайшей к T1 при прекращении действия ветра (справа). Расположение точек натурных наблюдений представлено на рис. III.3
3.2. Высокая геодинамическая опасность исследуемого региона Алтае-Саянской сейсмоактивной области (АССО) подтверждает необходимость создания на основе локальной мониторинговой сети, сформированной как комплекс специальных наблюдений за особенностями сейсмического и электромагнитного режима в изучаемой очаговой зоне подготовки сильного землетрясения, вычислительной технологии для выделения интегральных предвестников-структур в записях регистрируемых геофизических сигналах (рис. III.5).
В результате проведенных исследований разработана методика комплексного анализа предвестников-структур подготовки сильного землетрясения на основе анализа геодинамических полей, которая позволяет выделять особенности подготовки ожидаемого сильного землетрясения для исследуемой очаговой области. Вычислительная основа методики: алгоритмическое и программное обеспечение обработки и анализа данных о предвестниках-структурах подготовки сильного землетрясения на основе сейсмического и электромагнитного мониторинга, включающие быстрые алгоритмы вейвлет-преобразования и корреляционного анализа данных наблюдений, адаптированные к выявлению структур-предвестников изучаемых геодинамических процессов для выделенных очаговых зон сильных землетрясений АССО.
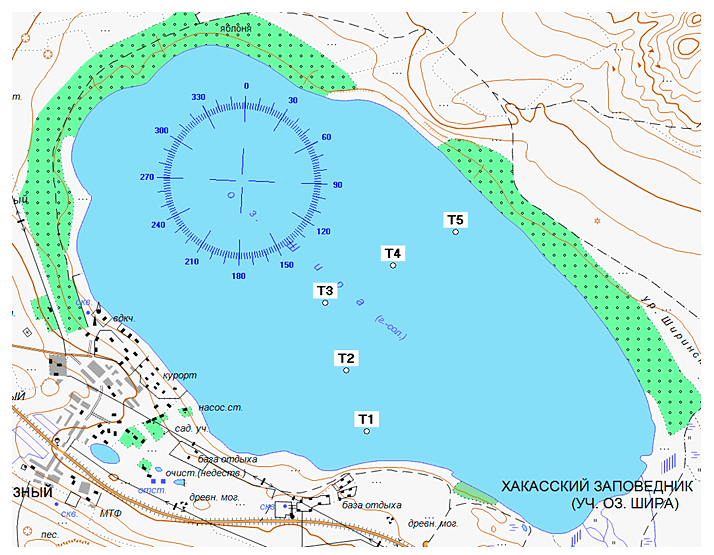
Рис. III.3. Картина расположения точек постановки термодатчиков с 13 по 29 июня 2013 г.
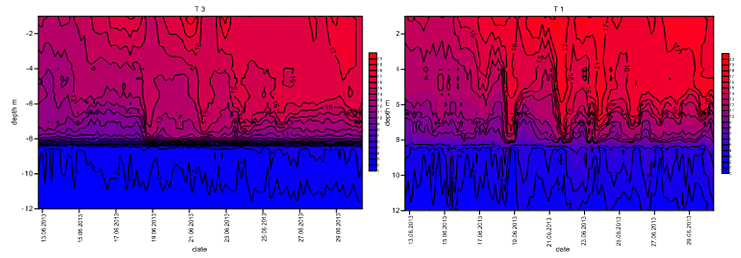
Рис. III.4. Данные с датчиков температуры в точке Т3 до глубины 12 м (слева) и точке Т1 до дна (справа)
В итоге, методика сравнительного анализа и интерпретации предвестников-структур подготовки сильного землетрясения представляется следующим образом: по данным сейсмического мониторинга выделяется зона подготовки землетрясения, где в сейсмическом процессе (форшоки) выявляется предвестник-структура подготовки основного землетрясения в виде формирования закономерности, а также в поле ЕИЭМПЗ при подготовке землетрясения выделяется аномальное изменение суточного хода электромагнитного сигнала. Исследование инструментальных данных ЕИЭМПЗ проводится в несколько стадий: преобразование исходных данных для дальнейшей обработки; преобразование данных — фильтрация и построение диаграмм «зависимости счета импульсов ЕИЭМПЗ от времени»; далее выполняется построение и анализ вейвлет-диаграмм сигналов ЕИЭМПЗ. Затем выполняется сравнительный анализ ЕИЭМПЗ и сейсмических данных для исследуемой очаговой области: построение номограмм для выделения предвестников-структур на основе корреляционного анализа данных наблюдений.
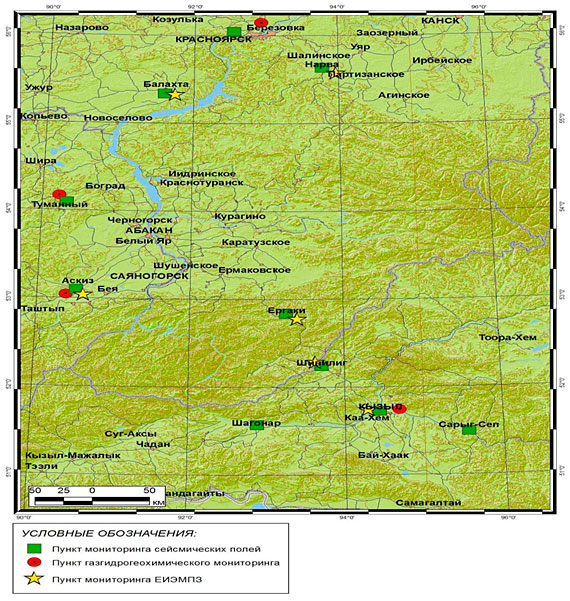
Рис. III.5. Схема сети геодинамического мониторинга на Алтае-Саянском полигоне
Разработанная методика использовалась для решения основных задач геомониторинга очаговых зон сильных землетрясений АССО. Соответствующие расчеты выполнялись с использованием разработанного алгоритмического и программного обеспечения для построения вейвлет-диаграмм и оценки параметров автокорреляционной функции исходных данных (рис. III.6- III.7). В качестве примера на рис. III.6 приведены данные сейсмического мониторинга и ЕИЭМПЗ по станции Орье; вейвлет-спектр на основе производных функции Гаусса для ЕИЭМПЗ; вейвлет-спектр Хаара для ЕИЭМПЗ; вейвлет-спектр MHAT для ЕИЭМПЗ, момент изучаемого землетрясения обозначен красной стрелкой. На представленной диаграмме (расчеты для вейвлета на основе производной функции Гаусса) видно, что момент землетрясения четко выделяется по резкому изменению частотного состава на области формирования закономерности-структуры в сейсмическом процессе.
Для изучения длительности и частотной структуры сигнала используется автокорреляционная функция (АКФ). Функция АКФ во временной области в интервале времени $\textit{t}{}_{1}-\textit{t}{}_{2}$ представляется в виде: $R(\tau )=\int _{t_{1} }^{t_{2} }f(t) f(t+\tau )dt,$ где $\textit{$\tau$} = 0$ — $\textit{T}$. АКФ — четная функция, поэтому при расчете ее в окне конечной длины с увеличением $\tau$ в выражении для $\textit{f}(\textit{t+$\tau$})$ входит меньше членов, что приводит к ухудшению оценок. Нормированная функция АКФ вычисляется по формуле: $R_{n}(\tau) = R(\tau)/R(0)$. Для анализа используются несколько характеристик АКФ: радиус корреляции r, который вычисляется по АКФ следующим способом: $r_{1} =\int _{0}^{T}R^{2} (t) \, dt, r_{2} =\int _{0}^{T}\left|R(t)\right| \, dt$. Оценивается также коэффициент «изломанности» АКФ х, который определяется по формуле $x=\, \left(\int _{0}^{T}\, \left[R'(t)\right]^{2} dt \right)^{{1\mathord{\left/ {\vphantom {1 2}} \right.} 2} }$. Оценки выполняются в рамках программного обеспечения, где реализован алгоритм быстрого расчета АКФ как для данных о землетрясении, так и для сигналов другой природы.
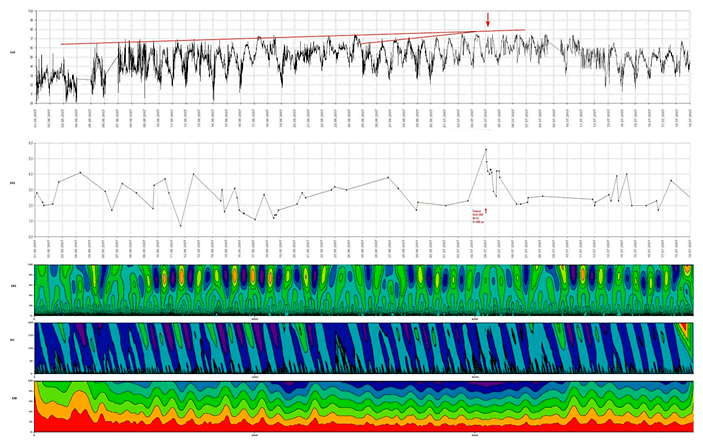
Рис. III.6. Сравнительная диаграмма вейвлет-спектров с данными геомониторинга по станции Орье
Предложенный критерий для выделения предвестника в поле ЕИЭМПЗ на основе функции АКФ для изучаемого землетрясения показан на рис. III.7. Показано значимое разделение поля значений параметров функции АКФ на две области: область до возникновения закономерности в сейсмическом процессе (I) и область формирования закономерности-структуры данных о сейсмическом процессе (II).
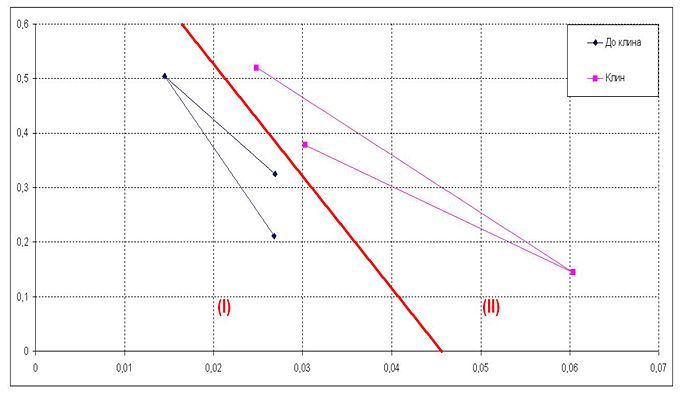
Рис. III.7. Оценка параметров предвестника-структуры на основе АКФ
Разработана вычислительная методика для сравнительного анализа данных геомониторинга комплекса геофизических предвестников процесса подготовки сильного землетрясения для исследуемой очаговой области. (К. В. Симонов)
Основные публикации:
- Андреев В. К., Бекежанова В. Б.
Устойчивость неизотермических жидкостей (обзор) // ПМТФ, 2013. — Т. 54. — № 2. — P. 3-20. - Lemeshkhova E. N.
Сombined motion of three viscous heat-conducting liquids in a flat layer // J. of Siberian Federal University. Mathematics and Physics, 2013. — Vol. 2. — № 6. — С. 211–219 . - Шанько Ю. В.
Обобщенные функционально-инвариантные решения двумерного неоднородного волнового уравнения // Сибирский журнал индустриальной математики, 2013. — Т. 16. — № 1. — С. 126–137 . - Баранов В. И., Голенко Н. Н., Компаниец Л. А., Пака В. Т., Якубайлик Т. В.
Пространственно-временная изменчивость основных характеристик озера Шира в сезоне 2911–201 2 гг. // Вестник Бурятского гос. ун-та. Математика, Информатика, 2013. — № 9. — С. 148–156 .
(Отделы Дифференциальных уравнений механики, Вычислительных моделей в гидрофизике)
| К началу | |