| ИВМ СО РАН | Поиск |
| Отчеты ИВМ СО РАН |
Отчет ИВМ СО РАН за 2013 год
Гранты российских научных фондов
- Гранты РФФИ
- Проект РФФИ №
11–01–00 053 — «Численное моделирование термомеханических процессов в средах с микроструктурой на суперкомпьютерах» - Грант РФФИ №
11–01–00 106-а — «Численное моделирование динамических процессов в больших электрических сетях» - Грант РФФИ №
11–01–00 224-а — «Метод траекторий и конечных элементов для решения уравнений Навье-Стокса для вязкого теплопроводного газа» - Грант РФФИ №
11–01–00 283-а — «Структуры и устойчивость течений сопряженных задач тепломассообмена» - Грант РФФИ №
12–05–00 152-а — «Математическое моделирование влияния магнитосферных и ионосферных процессов на атмосферные электрические поля» - Проект РФФИ
12–01–31 069_мол_а — «Влияние эффекта Соре на режимы конвективных течений в многокомпонентных смесях» - Грант РФФИ
12–07–31 143_мол_а — «Разработка методов и средств концептуального OLAP-моделирования для информационно-аналитической поддержки предупреждения возникновения и смягчения последствий чрезвычайных ситуаций» - Проект РФФИ
13–01–07 002 — «Издание монографии «Термодиффузия в смесях: уравнения, симметрии, решения и их устойчивость» - Проект РФФИ
13–05–00 853 — «Внутренние волны и их влияние на биологические компоненты меромиктического озера» - Проект РФФИ
12–01–00 648-а — «Численный, групповой и геометрический анализ уравнений гидродинамического типа» - Проект РФФИ
13–01–00 246 — «Математическое моделирование вырождения свободных турбулентных течений» - Гранты Красноярского краевого фонда поддержки науки и научно-технической деятельности
Гранты РФФИ
Проект РФФИ №
№ гос. регистрации 01201159524
Руководитель: д.ф.-м.н., профессор В. М. Садовский
Разработаны новые дискретные модели и вычислительные алгоритмы для анализа деформирования и разрушения линейно-армированных композиционных материалов на основе уравнений теории упругости структурно неоднородной среды.
На основе уравнений нелинейной динамики упругой среды, учитывающих вращательные степени свободы частиц микроструктуры материала, построена упрощенная математическая модель для описания волновых движений нематического жидкого кристалла под действием слабых механических и температурных возмущений. Упрощающее предположение модели состоит в том, что в качестве параметров термодинамического состояния жидкого кристалла взяты объемная деформация, угол относительного поворота частиц (доменов соориентированных молекул) и энтропия. В рамках этого предположения получены уравнения плоского и пространственного деформирования для описания процессов распространения акустических волн в жидкокристаллической среде, сопровождающихся конечными поворотами частиц.
Установлено, что при плоской деформации жидкого кристалла в геометрически линейном приближении модели касательное напряжение удовлетворяет уравнению Клейна-Гордона, описывающему осцилляционный характер вращения частиц. С помощью этого уравнения показано, что если в начальный момент времени кристалл находится в естественном ненапряженном состоянии при отсутствии объемных сил и моментов, то касательное напряжение, которое полностью определяет вращательное движение частиц, остается равным нулю всегда во всех внутренних точках области. Показано также, что влияние температурного поля на повороты частиц осуществляется только через граничные условия задачи. Отсюда следует, что невозможно изменить ориентацию молекул жидкого кристалла за счет теплового воздействия на свободной от напряжений границе среды. Таким образом, судя по предложенной модели, эффект ориентационной термоупругости нематического жидкого кристалла, который обсуждается в ряде современных работ физиков-теоретиков и экспериментаторов, следует связывать с возникновением касательных напряжений на границе.
Выполнен численный анализ уравнения Клейна-Гордона, по результатам которого сформулирована гипотеза о возможности резонансного возбуждения жидкого кристалла на частоте собственных колебаний вращательного движения частиц (рис. VI.1).
Для численного решения уравнений модели разработаны параллельные алгоритмы и компьютерные программы, ориентированные на многопроцессорные вычислительные системы с графическими ускорителями. При дискретизации уравнений шаги разностной сетки согласовываются с характерным размером частиц микроструктуры жидкокристаллической среды, что является необходимым условием физической корректности численных решений. В результате получаются задачи большой размерности, требующие высокопроизводительных вычислений. В качестве демонстрационного примера на рис. VI.2 приведены результаты расчетов стационарного температурного поля в жидком кристалле, частицы которого повернуты под углом 60° для различных соотношений коэффициентов теплопроводности в направлении молекул и в ортогональном направлении. Начальное поле температуры считалось однородным, в выделенных зонах на границе области задавалось равномерное распределение температуры.
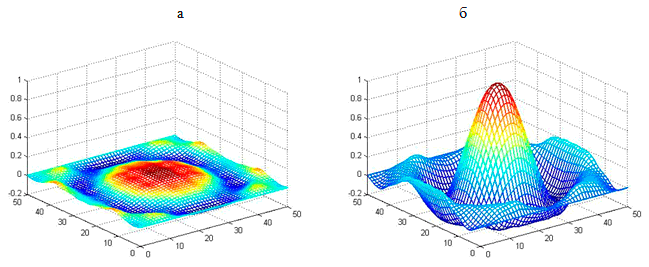
Рис. VI.1 Возбуждение жидкого кристалла под действием локализованного момента: а — нерезонансная частота, б — резонансная частота
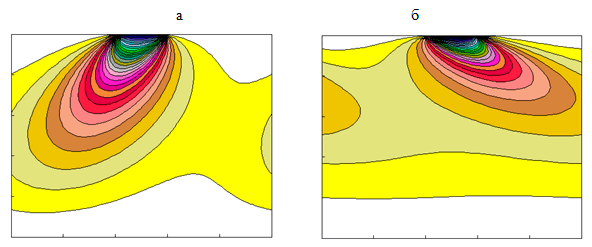
Рис. VI.2. Линии уровня температуры в жидком кристалле при разных соотношениях между коэффициентами теплопроводности $\kappa $ и $\kappa '$ в направлении ориентации молекул и в противоположном направлении: а — $\kappa=5\, \kappa '$, б — $\kappa ={\kappa '\mathord{\left/ {\vphantom {\kappa ' 5}} \right.} 5}$
Основные публикации:
- Садовский В. М., Садовская О. В.
Об акустическом приближении термомеханической модели жидкого кристалла // Физическая мезомеханика, 2013. — Т. 16. — № 3. — С. 55-62. - Матвеев А. Д.
Смешанные дискретные модели в анализе упругих трехмерных неоднородных тел сложной формы // Вестник ПНИПУ. Механика, 2013. — № 1. — С. 182–195 . - Sadovskii V. M.
On the acoustic approximation of thermomechanical model of a liquid crystal // APM 2013: Proceedings of the XLI Summer School — Conf. «Advanced Problems in Mechanics». Institute for Problems in Mechanical Engineering of RAS, St.-Petersburg, 2013. — P. 492–499 .
(Отдел вычислительной механики деформируемых сред)
| К началу | |
Грант РФФИ №
№ гос. регистрации 01201159527
Руководитель: д.ф.-м.н., профессор Е. А. Новиков
Создан современный интерфейс для расчета, анализа и оптимизации электрических сетей. Построен аддитивный метод третьего порядка для решения жестких неавтономных задач, который реализован на многопроцессорной ЭВМ. Проведены расчеты реальных электрических сетей.
Основные публикации:
- Колбасинский Д. В., Кнауб Л. В., Новиков Е. А.
Закон оптимального управления электроподвижным составом с реостатно-контакторной системой управления // Электроника и электрооборудование транспорта, 2013. — № 1. — С. 23-26. - Колбасинский Д. В., Новиков Е. А.
Численное моделирование разгона электроподвижного состава с реостатно-контакторным управлением // Системы управления и информационные технологии, 2013. — № 2(52). — С. 83-88.
(Отдел вычислительной математики)
| К началу | |
Грант РФФИ №
№ гос. регистрации 01201159525
Руководитель: член-корреспондент РАН В. В. Шайдуров
Блок 1. Численное решение нестациогарных уравнений Навье-Стокса для вязкого теплопроводного газа (В. В. Шайдуров, Г. И. Щепановкая, М. В. Якубович).
Течение жидкости в каналах со скачкообразным расширением сечения встречается во многих технических устройствах и сооружениях. Резкое расширение сечения способно вызвать отрыв потока и существенно изменить его кинематическую структуру. В силу большой практической значимости такие течения изучались теоретически и экспериментально как для ламинарных, так и для турбулентных режимов движения несжимаемой и сжимаемой жидкости. В настоящее время стало ясно, что при постановке задач расчета отрывных течений с вихревыми образованиями необходимо использовать не приближенные уравнения пограничного слоя, а полные уравнения Навье-Стокса. Однако использование более сложных математических моделей приводит к возрастанию вычислительных затрат. Как следствие, это вызывает необходимость разработки и создания специальных численных методов решения этих уравнений и применения эффективных численных методов и алгоритмов.
Следует отметить, что система двумерных уравнений Навье-Стокса для вязкого теплопроводного газа включает четыре дифференциальных уравнения в частных производных, вытекающих из законов сохранения массы, количества движения и внутренней энергии газа. Предложенная в работе замена искомых функций в уравнениях неразрывности и внутренней энергии переводит закон сохранения массы и полной энергии из терминов пространства норме $L_{1}$ в термины гильбертова пространства $L_{2}$. Впоследствии это значительно упрощает обоснование устойчивости и сходимости.
В настоящей работе для аппроксимации полной (субстанциональной, или Лагранжевой) производной по времени в каждом уравнении системы используется метод траекторий, который заключается в аппроксимации этой производной с помощью разностной производной назад по времени вдоль траектории движения частицы. Дискретизация по пространству остальных слагаемых уравнений Навье-Стокса на каждом временном слое осуществляется методом конечных элементов с кусочно-билинейными базисными функциями и применением простых квадратурных формул. Для решения систем алгебраических уравнений используется метод Якоби с улучшенным начальным приближением внутри внешних итераций по нелинейности.
Как следует из тестовых расчетов, модификация уравнений Навье-Стокса обеспечивает повышение точности приближенного решения по сравнению с погрешностью для немодифицированных уравнений. А применение комбинации методов траекторий и конечных элементов позволяет построить алгоритм, довольно эффективный с вычислительной точки зрения. Численная реализация построенных алгоритмов осуществлена для высокопроизводительных вычислительных кластеров. На рис. VI.3 — VI.6 приведены изолинии плотности в сверхзвуковом течении вязкого теплопроводного газа в плоском канале с прямоугольным уступом для разных параметров.
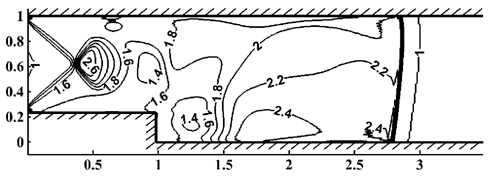
Рис. VI.3. Изолинии плотности для моментов времени t = 4 при M = 2, Re = 2 × 103
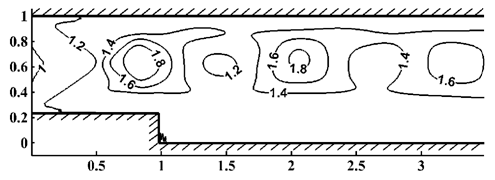
Рис. VI.4. Изолинии плотности для моментов времени t = 50 при M = 2, Re = 2 × 103
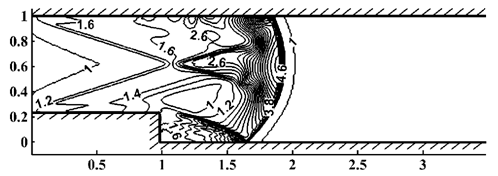
Рис. VI.5. Изолинии плотности для моментов времени t = 4 при M = 4, Re = 104
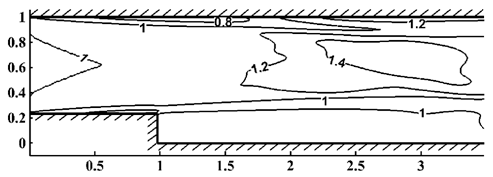
Рис. VI.6. Изолинии плотности для моментов времени t = 50 при M = 4, Re = 104
Разработана, теоретически обоснована и экспериментально проверена интегральная численная схема из семейства полулагранжевых методов для решения двумерного (по пространству) уравнения неразрывности. Метод основан на точном тождестве двух пространственных интегралов, области интегрирования которых лежат на соседних слоях по времени:
\[\int _{\Omega }\rho \left(t_{k} ,x,y\right)\, d\Omega =\int _{Q}\rho \left(t_{k-1} ,x,y\right)\, dQ ,\]
где $\rho \left(t,x,y\right)$ — искомая функция плотности, $\Omega $ — произвольный прямоугольный четырехугольник. $Q$ — некоторый криволинейный четырехугольник. Для учета краевых условий рассмотрена квадратная вычислительная область $\left[0,1\right]\times \left[0,1\right]$ с ненулевыми значениями скорости на границах $x=0$ и $x=1$. Доказано модифицированное тождество:
\[\int _{\Omega }\rho \left(t_{k} ,x,y\right)\, d\Omega =\int _{Q}\rho \left(t_{k-1} ,x,y\right)\, dQ +\int _{I}\left(\rho u\right)\left(t,x,y\right)\, dI ,\]
где $u\left(t,x,y\right)$ — функция скорости, $R$ — некоторый криволинейный четырехугольник, лежащий в плоскости границы. Порядок сходимости зависит от асимптотической точности вычисления интегралов. При построении схемы использована прямоугольная сетка и исследован случай билинейной аппроксимации $\rho _{h}^{I} $ подынтегральный функции $\rho \left(t_{k-1}, x,y\right)$ на каждом слое по времени. В этом случае, численное решение $\rho _{h} $ в узле $\left(t_{k}, x_{i}, y_{j} \right)$определяется по формуле:
\[\rho _{i,j}^{k} =\frac{1}{{\rm mes}\left(\Omega _{i,j} \right)} \int _{P_{ij}^{k-1} }\rho _{h}^{I} \left(t_{k-1} ,x,y\right)\, dP +\frac{1}{{\rm mes}\left(\Omega _{i,j} \right)} \int _{L_{i,j}^{k} }\left(\rho u\right)^{I} \left(t,x,y\right)\, dL ,\]
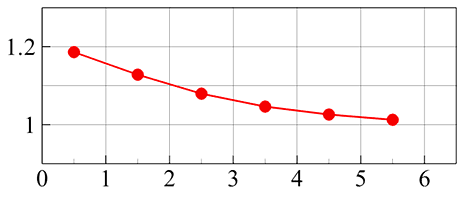
Рис. VI.7. Порядок сходимости схемы
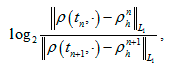
характеризующая порядок сходимости численного решения к точному. При этом условие Куранта-Фридрихса-Леви выполняется без использования алгебраических соотношений, связывающих шаги по времени и по пространству.
Таким образом, предложенная схема не ограничивает шаг по времени в зависимости от значений функции скорости, что является удобным средством, сокращающим вычислительные затраты для решения задач с большими значениями скоростей. При проведении численных экспериментов это позволило для ряда тестовых задач увеличить шаг по времени до величины в десять раз превышающей максимальное допустимое значение, соответствующее условию Куранта-Фридрихса-Леви. При этом сравнение со схемой набегающего потока (upwind scheme) показало, что при одинаковых значениях шага по времени максимальная величина абсолютной погрешности отличается незначительно, до 20%. Другим важным свойством разработанной схемы является выполнение дискретного аналога балансового отношения на каждом слое по времени. Среди прочих преимуществ метода следует отметить, что пространственные сетки на соседних слоях по времени не зависят друг от друга и могут меняться от слоя к слою. Кроме того, процесс распараллеливания и обобщения на трехмерный случай не представляет собой принципиальной сложности.
Блок 3. Выбор итерационного параметра при решении обратной некорректной задаи о граничной функции (Е. Д. Карепова, Е. В. Дементьева).
Для осредненных по глубине уравнений приливной динамики рассмотрена обратная задача на восстановление граничной функции, описывающей влияние океана на открытую границу вычислительной области. Для ее решения на каждом шаге по времени предложен итерационный численный алгоритм, восстанавливающий граничную функцию на всей морской границе по данным наблюдений за возвышением свободной поверхности, заданным на части границы по морю.
В отчетный период с целью выбора наиболее эффективной реализации алгоритма были предложены и исследованы две различные итерационные схемы на основе методов решения некорректных задач и три способа выбора основного итерационного параметра. Итерационный параметр $\textit{$\gamma $}$ выбирался методом подбора (МП), минимальных невязок (ММН) и методом из теории экстремальных задач (МЭЗ). Отметим, что метод МН является наиболее трудоемким в реализации и по объему вычислений, поскольку требует на каждой итерации дополнительного решения прямой и сопряженной задач для вычисления $\textit{$\gamma $}$. В МЭЗ требуется на каждом шаге итерации дополнительно вычислять отношение норм уже найденных решений. В МП не нужно проводить дополнительных вычислений для $\textit{$\gamma $}$, поскольку параметр $\textit{$\gamma $}$ полагается постоянным ($\textit{$\gamma$} = \textit{const}$).
Результаты численных экспериментов по скорости сходимости предложенного итерационного алгоритма в случае использования итерационных схем 1 и 2 и трех видов итерационных параметров $\textit{$\gamma $}$ приведены в табл. 1. В эксперименте в качестве «наблюдений» использовались гладкие, с пропуском и зашумленные данные и граничная функция $\textit{d}$ восстанавливалась в пространствах $L_{2} $, $H^{1} $, $H^{1/2} $.
Из табл. 1 видно, что метод для вычисления оптимального итерационного параметра $\textit{$\gamma $}$ следует выбирать в зависимости от пространства восстановления граничной функции. При восстановлении $\textit{d}$ из $L_{2} $ лучший результат по скорости сходимости достигается при выборе $\textit{$\gamma $}$ методом минимальных невязок, при восстановлении из $H^{1}$ — методом из теории экстремальных задач, при восстановлении из $H^{1/2} $ — методом подбора.
Пример восстановления граничной функции $\textit{d}$ в пространствах $H^{1} $, $H^{1/2} $ по данным наблюдений с двумя пропусками приведен на рис. VI.8. Из него видно, что граничная функция $\textit{d}$ и возвышение свободной поверхности $\textit{$\xi$}$ восстанавливаются во всех точках морской границы. При этом на качество восстановленных данных влияет главным образом пространство поиска граничной функции $\textit{d}$.
| Пространство восстановления d | Итерационная схема | Данные наблюдений | $\textit{$\gamma$}$ по МП | $\textit{$\gamma$}$ по ММН | $\textit{$\gamma$}$ по МЭЗ |
|---|---|---|---|---|---|
| $\textit{d}$ из $L_{2}$ | Схема 1, 2 | гладкие | 9 | 3 | 9 |
| с пропуском | 9 | 3 | 9 | ||
| зашумленные | 9 | 3 | 19 | ||
| $\textit{d}$ из $H^{1}$ | Схема 1 | гладкие | 93 | 25 | 44 |
| с пропуском | 122 | 25 | 34 | ||
| Схема 2 | гладкие | 45 | 57 | 24 | |
| с пропуском | 60 | 81 | 29 | ||
| $\textit{d}$ из $H^{1/2}$ | Схема 1, 2 | гладкие | 11 | 9 | 60 |
| с пропуском | 13 | 9 | 58 | ||
| зашумленные | 45 | 32 | 50 |
Таблица 1. Количество итераций для сходимости итерационного алгоритма при восстановлении по данным наблюдений разного вида
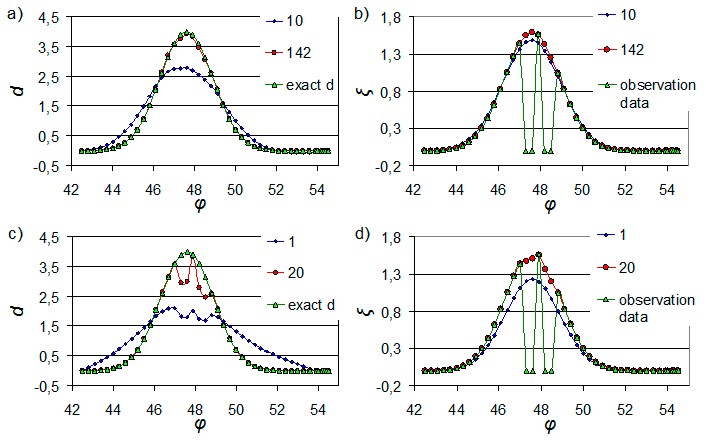
Рис. VI.8. Восстановление функций $\textit{d}$ (слева) и $\textit{$\xi$}$ (справа) на одной из жидких границ области по данным наблюдений, заданным с пропусками. В пространстве $H^{1}$ — a) и b); в пространстве $H^{1/2}$ — c) и d)
Основные публикации:
- Шайдуров В. В., Щепановская Г. И., Якубович М. В.
Численное моделирование течений вязкого теплопроводного газа в канале // Вычислительные технологии, 2013. — Т. 18. — № 4. — С. 77-90. - Синь B., Вяткин А. В., Шайдуров В. В.
Semi-Lagrangian Scheme for solving hyperbolic equation of first order // Молодой учёный, 2013. — № 9. — С. 6-13. - Dementyeva Е., Karepova E., Shaidurov V.
The Inverse Problem of a Boundary Function Recovery by Observation Data for the Shallow Water Model // ENUMATH 2013: 10-th European Conf. on Numerical Mathematics and Advanced Applications. Book of Abstracts. Ecole Polytechnique Federale de Lausanne (EPFL), Math. Inst. of Computat. Science and Engineering (MATHICSE), Lausanne, 2013. — P. 96-97.
(Отдел вычислительной математики)
| К началу | |
Грант РФФИ №
№ гос. регистрации 01201159523
Руководитель: д.ф.-м.н., профессор В. К. Андреев
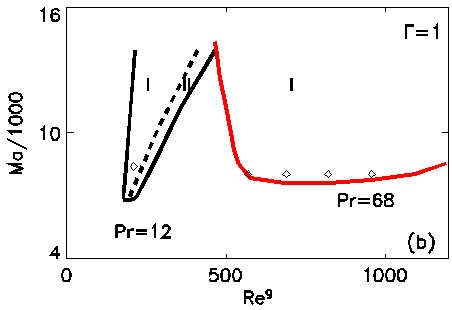
Рис. VI.9. Кривые устойчивости
1. Методами численного моделирования проведено комплексное исследование задачи о взаимодействии свободной границы жидкого моста с потоком газа. Рассмотрены характерные структуры течения, их характеристики в зависимости от скорости и направления потока газа, а также температурных условий. Обнаружено, что в случае, когда поток газа противонаправлен течению жидкости, образованной температурной зависимостью поверхностного натяжения, возникает колебательный режим с формированием вихревой структуры течения, двигающейся вдоль свободной границы. Выявлена зависимость области существования колебательного режима от скорости набегающего потока газа, температурных условий, а также свойств жидкости.
На рис. VI.9 показаны кривые устойчивости для силиконового масла (Pr = 68) и n-decane (Pr = 12).
На рис. VI.10 представлены трехвихревые структуры колебательного течения, образованные при обдуве жидкого моста со скоростью 0.75 и 1.5 м/с.
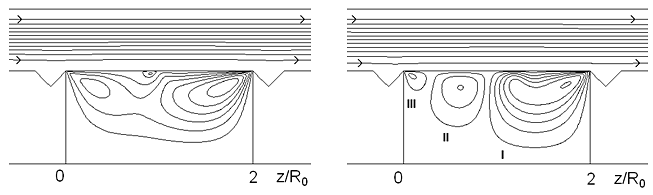
Рис. VI.10. Структуры колебательного течения
2. На основе методов численного моделирования рассмотрена задача о влиянии испарения жидкости со свободной поверхности цилиндрического неизотермического жидкого моста, обдуваемого соосным потоком газа. Полученные результаты демонстрируют качественное и количественное соответствие экспериментальным данным применительно к легкоиспаряющимся жидкостям (n-decane, ацетон). Эффект испарения приводит к охлаждению жидкости, увеличению градиентов температуры в приповерхностном слое жидкости и, как следствие, усилению конвективных процессов в жидком мосте. Определены параметры, при которых испарение приводит к появлению инверсионных процессов в жидкости с образованием переохлажденных областей. Исследовано влияение испарения на усточивость конвективного течения.
На рис. VI.11 показаны поле температуры в среднем сечении а также поверхность с температурой 300.3 К для задачи без учета испарения, рис. VI.11, а), и с учетом испарения при 0.0011 об.%/с, рис. VI.11, б). Видно, что область холодной жидкости под изоповерхностью 300.3 К в случае учета испарения занимает гораздо больший объем.
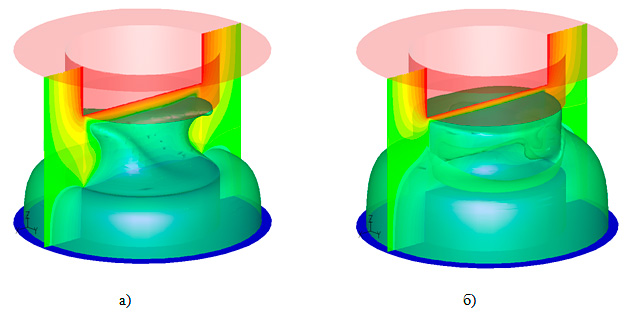
Рис. VI.11. Поле температуры в среднем сечении и поверхность с температурой 300,3 К для задачи при 0.0011 об.%/с а) без учета испарения: б) с учетом испарения
Основные результаты представлены на конференции International Topical Team Workshop: Two-phase systems for ground and space applications. (Ю. А. Гапоненко)
3. Рассмотрена задача о возникновении конвекции в цилиндрическом контейнере. Для ее решения был применен метод разделения переменных. В результате получено однородное дифференциальное уравнение шестого порядка с постоянными коэффициентами со сложными граничными условиями. Для случая, когда возмущения монотонны, получено аналитическое выражение для критических чисел Марангони. Разобран случай, когда система находится в состоянии невесомости, для которого доказано, что с увеличением радиуса цилиндра критические числа Марангони стремятся к известным числам Марангони для бесконечного слоя. (Е. П. Магденко)
4. Рассмотрена задача о течении тонкой жидкой пленки, увлекаемой потоком газа. На основе математической модели с полным энергетическим условием на поверхности раздела
\[k_{g} \frac{\partial T_{g} }{\partial n} (x,h(x))-k_{l} \frac{\partial T_{l} }{\partial n} (x,h(x))=\kappa T\nabla _{11} \cdot v\]
исследовано влияние термокапиллярных сил на характер возникающей неустойчивости. Конвективные движения вблизи поверхности раздела жидкость-газ могут развиваться за счет процесса высвобождения/поглощения теплоты при локальных изменениях площади межфазной поверхности. Изучено влияние приращений поверхностной внутренней энергии на тип неустойчивостей пленочного течения. Для этого исследована линейная устойчивость совместного течения пленки и газа и построена карта возможных режимов неустойчивости. Установлено, что наиболее опасной является термокапиллярная мода. На основе проведенной селекции мод и результатов линейного анализа рассчитаны закритичные режимы. При термокапиллярной неустойчивости в пленке формируются продольные валы, оси которых параллельны направлению основного течения. В коротковолновой области кризис течения сопровождается формированием поперечных бегущих волн, которые распространяются в противоположном основному течению направлении. При этом наблюдается сосуществование продольных валов, индуцируемых силами Марангони, и бегущих поперечных волн.
Таким образом, градиенты сил межфазного натяжения, возникающие под влиянием теплоты, поглощаемой или выделяющейся при локальной изменениях площади межфазной поверхности, способствуют формированию волновых режимов. (В. Б. Бекежанова)
Основные публикации:
- Shevtsova V., Gaponenko Yu., Nepomnyashchy A.
Thermocapillary flow regimes and instability caused by a gas stream along the interface // J. of Fluid Mechanics, 2013. — V. 14. — P. 644–670 . - Магденко Е. П.
Решение линеаризованной сопряжённой задачи конвекции в цилиндрах // Материалы LXVI Междунар. науч. конф. «Герценовские чтения — 2013». — СПб: РГПУ, 2013. — С. 115–118 . - Андреев В. К., Бекежанова В. Б.
О решении со свободным параметром уравнений конвекции в вертикальном цилиндре при объемном прогреве // ПММ, 2013. — Т. 77. — Вып. 6. — С. 832–841 .
(Отдел дифференциальных уравнений механики)
| К началу | |
Грант РФФИ №
№ гос. регистрации 01201260709
Руководитель: д.ф.-м.н., профессор В. В. Денисенко
Построены распределения электрических полей в ионосфере Земли, которые являются замыканием глобальной электрической цепи, генерируемой грозовой активностью. Критически проанализированы некоторые известные модели, дающие иной масштаб проникновения поля из приземной атмосферы в ионосферу.
Создана математическая модель возникновения и развития неустойчивых изгибных деформаций токового слоя магнитосферного хвоста. Показано, что неустойчивость возникает в областях отрицательного градиента нормальной компоненты магнитного поля в хвосте магнитосферы. Данная неустойчивость может существенно возмущать конфигурацию магнитного поля в хвосте магнитосферы, а также влиять на ионосферные электрические поля и токи.
Основные публикации:
- Денисенко В. В.
О проникновении атмосферного электрического поля в ионосферу // Материалы всерос. конф. «Глобальная электрическая цепь». Геофизическая обсерватория «Борок» — филиал Института физики Земли им. О. Ю. Шмидта — Ярославль, 2013. ISBN 978-5-91730–265 -2. — С. 8-9. - Harris B., Farrugia C. J., Erkaev N. V., Torbert R. B.
Observational aspects of IMF draping-related magnetosheath accelerations for northward IMF. Ann. Geophys., 31, 1-11, 2013, www.ann-geophys.net/31/1/2013/, doi:10.5194/angeo-31-1-2013. - Korovinskiy D. B. Semenov V. S., Divin A., Lapenta G., Erkaev N., Markidis S., Ivanova V. V., Biernat H. K., Ivanov I. B., Zellinger M.
MHD modeling of the double-gradient (kink) magnetic instability // J. of Geophysical Research: Space Physics, VOL. 118, 1146-1, doi:10.1002/jgra.50206, 2013.
(Отдел вычислительной математики)
| К началу | |
Проект РФФИ
№ гос. регистрации 01201275321
Руководитель: к.ф.м.н. И. И. Рыжков
При экспериментальном измерении коэффициентов диффузии и термодиффузии часто используется конфигурация плоского слоя, подогреваемого снизу или сверху. Основным требованием к эксперименту является чисто диффузионный тепломассообмен в исследуемой смеси. Однако неоднородности температуры и концентрации в поле силы тяжести могут привести к возникновению конвективного движения. В связи с этим является актуальной задача об устойчивости механического равновесия в плоском слое смеси при различных режимах подогрева. Кроме того, представляет интерес изучение структур конвективных течений, возникающих за порогом неустойчивости.
На первом этапе была исследована устойчивость механического равновесия в бесконечном плоском слое, подогреваемом снизу (или сверху) в поле силы тяжести. Движение смеси описывается уравнениями Навье — Стокса и тепломассообмена с учетом перекрестной диффузии и эффекта Соре. В основном состоянии движение отсутствует, при этом постоянный градиент температуры в слое приводит к возникновению постоянных градиентов концентрации компонентов благодаря эффекту Соре.
Проведен линейный анализ устойчивости равновесия относительно малых возмущений. Найдены критические параметры неустойчивости (число Рэлея, волновое число и частота колебаний) с помощью аналитических и численных методов.
На втором этапе было проведено исследование неустойчивости механического равновесия в замкнутой полости с помощью численного моделирования. Рассматривалась двумерная прямоугольная полость с соотношением сторон $L/H=10$, где $L$ — длина полости, $H$ — высота полости (рис. VI.12). На границах полости ставились условия прилипания и отсутствия потока массы компонентов смеси. На горизонтальных границах задавалась температура, а на вертикальных границах — отсутствие потока тепла.
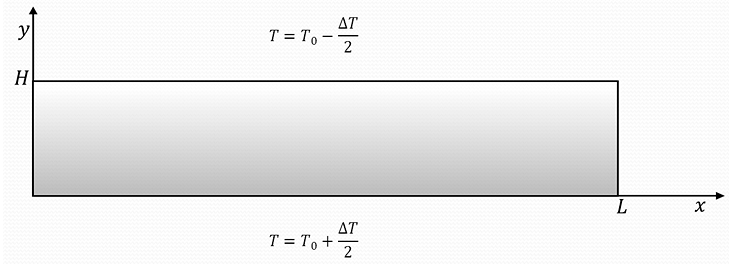
Рис. VI.12. Прямоугольная полость с разностью температур между горизонтальными стенками
Аппроксимация уравнений Навье-Стокса по пространству производилась с использованием смещённых сеток. Горизонтальная скорость $\textit{u}$ определялась в центре вертикальных граней ячейки, вертикальная скорость $\textit{v}$ — в центре горизонтальных граней ячейки, давление $\textit{p}$ определяется в центре ячейки, а температура и концентрации определяются в узлах сетки. Алгоритм расчёта строился на основе метода расщепления по физическим процессам. На первом этапе для расчёта нелинейного переноса в уравнениях импульса использовалась явная схема. На втором этапе учитывалось движение под действием вязких сил. Для расчёта этого движения применяется полностью неявная схема. На третьем этапе производилась корректировка поля скоростей для того, чтобы выполнить условие несжимаемости. Этот этап сводится к решению уравнения Пуассона для давления с граничным условием Неймана. Для расчёта изменения температуры и концентраций использовалась неявная схема расщепления. Расчеты проводились на сетке 200 $\times$ 20 с шагом по времени $0.002\tau _{\nu } $, где $\tau _{\nu }$ — вязкое время.
В качестве примера рассмотрим неустойчивость в тройной смеси с параметрами $\psi _{1} =0.4,{\rm \; \; }\psi _{{\rm 2}} =-0.6,{\rm \; \; }\Pr =10,{\rm \; \; Sc}_{{\rm 1}} {\rm =100,\; \; Sc}_{{\rm 2}} =1000$. Здесь Pr — число Прандтля, ${\rm Sc}_{j} $ — числа Шмидта, $\psi _{j} $ — отношения разделения компонентов, характеризующие эффект Соре $j=1,2$. В данной смеси первый компонент концентрируется у нагретой границы, а второй — у холодной границы в результате термодиффузии. Согласно результатам линейного анализа, критические параметры неустойчивости для данной смеси при подогреве снизу ${\rm Ra}_{c} {\rm =\; }1825,{\rm \; \; }k_{c} =3.18;{\rm \; \; }\omega _{{\rm c}} =0.977$.
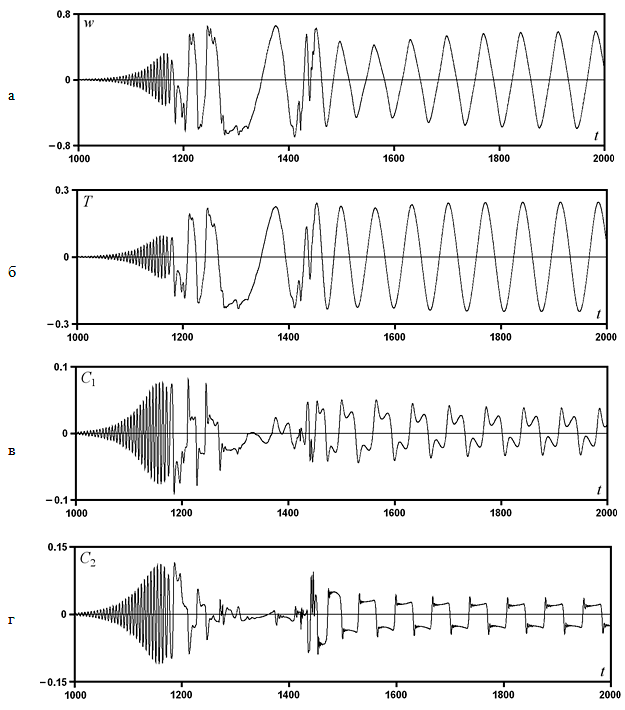
Рис. VI.13. Зависимость от времени безразмерных значений вертикальной скорости (а), температуры (б), коцентрации первого (в) и второго (г) компонентов тройной смеси в точке $x=5$, $y=0.5$ (центр полости). Параметры смеси: $\psi_{1}=0.4$, $\psi_{\rm 2}=-0.6$, $Pr =10$, $Sc_{1}=100$, $Sc_{2}=1000$. Число Рэлея ${\rm Ra}=1900$
На рис. VI.13 показана зависимость от времени значений вертикальной скорости, температуры и концентрации компонентов смеси от времени в центре полости для числа Рэлея ${\rm Ra}=1900$. Расчеты показывают, что неустойчивость начинается развиваться с момента времени $t\approx 1000$ (единице времени соответствует характерное вязкое время $\tau _{\nu } =L^{2} /\nu $). На промежутке $1000 \lt t \lt 1160$ наблюдается экспоненциальный рост колебательных возмущений с периодом $\tau =6.205$, что хорошо согласуется с результатами линейного анализа $\tau _{c} =2\pi /\omega _{c} =6.431$. При $t>1160$ в системе начинают преобладать нелинейные эффекты. После нерегулярных колебаний начиная с момента времени $t\approx 1500$ возникает периодическое движение (бегущая волна). Структура полей скорости, температуры и концентрации при $t=2000$ показана на рис. VI.14. В слое наблюдается структура из конвективных ячеек. Вращение жидкости в соседних ячейках происходит в противоположных направлениях. Заметим, что поле концентрации первого компонента более размыто, чем второго, в связи с тем, что его диффузионные свойства лучше.
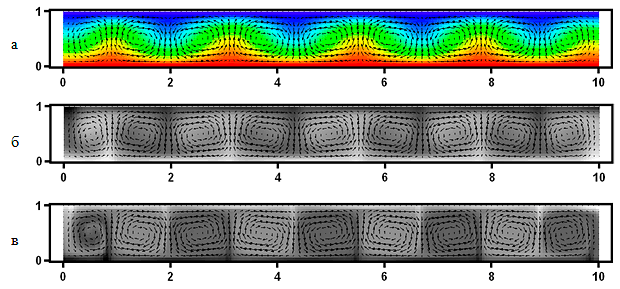
Рис. VI.14. Структура полей скорости, температуры (а) и концентрации первого (б) и второго (в) компонентов тройной смеси с параметрами $\psi_{1}=0.4$, $\psi_{2}=-0.6$, $(\Psi =-0.2)$, $Pr =10$, $Sc_{1}=100$, $Sc_{2}=1000$. Число Рэлея ${\rm Ra}=1900$, момент времени $t=2000$. Светлые области на рис. б, в соответствуют бульшим значениям концентрации, темные области — меньшим
Численные расчеты для числа Рэлея ${\rm Ra}=1850$ показали, что на промежутке $0 \lt t \lt 2000$ неустойчивость не развивается. Таким образом, на основании численных расчетов критическое число Рэлея для замкнутой полости с соотношением сторон $L/H=10$ может быть оценено как ${\rm Ra}\approx 1900$, что на 4 % выше значения, полученного на основе линейного анализа ${\rm Ra}_{c} = 1825$ для бесконечного слоя. Расчеты для чисел Рэлея, значительно превышающих критическое значение, показали, что на больших временах режим бегущей волны сменяется стационарной структурой из конвективных ячеек.
Основные публикации:
- Рыжков И. И.
Термодиффузия в смесях: уравнения, симметрии, решения и их устойчивость. — Новосибирск: СО РАН, 2013. — 200 с. - Рыжков И. И.
Длинноволновая неустойчивость плоского слоя многокомпонентной смеси с эффектом Соре // Известия РАН: Механика жидкости и газа, 2013. — № 4. — С. 64-79. - Рыжков И. И., Зализняк В. Е.
Численное моделирование конвективной неустойчивости в многокомпонентных смесях с эффектом Соре // Тез. докл. XVIII Зимней школы по механике сплошных сред. — Пермь, 2013. — С. 296.
(Отдел дифференциальных уравнений механики)
| К началу | |
Грант РФФИ
№ гос. регистрации 01201274703
Руководитель: к.т.н. Коробко
Исполнители: А. В. Коробко, Т. Г. Пенькова, А. И. Белорусов, Е. А. Грузенко
Разработан встраиваемый программный модуль построения и управления интегральной OLAP-моделью на основе предложенного метода концептуального OLAP-моделирования предметной области. В основу программных средств легли модифицированные и формализованные алгоритмы теории анализа формальных понятий для обнаружения концептов и построения концептуальной решетки: итеративная реализация метода Крайеса [Krajca, 2008] и алгоритм формирования решетки концептов NEIGHBORS [Linding, 2000]. Интеграция с технологией OLAP позволяет использовать концептуальную решетку OLAP-кубов для поддержки формирования пользовательских аналитических запросов, путем формирования множеств дополнительных объектов анализа, которые совместимы с ранее выбранными показателями и измерениями. Выполнено построение интегральной OLAP-модели для задачи мониторинга чрезвычайных ситуаций, состояния объектов окружающей среды и техносферы Красноярского Края. Предложена архитектура системы, обеспечивающая взаимодействие оригинального программного модуля управления интегральной OLAP-моделью и пользовательского web-интерфейса для поддержки адаптивного формирования аналитических запросов.
Основные публикации:
- Коробко А. В., Пенькова Т. Г.
Представление и применение знаний о кубах-концептах для поддержки адаптивного манипулирования объектами анализа OLAP // Вестник СибГАУ, 2013. — № 3(49). — С. 51-57. - Коробко А. В., Пенькова Т. Г., Ничепорчук В. В.
Оперативный аналитический контроль состояния объектов техносферы и окружающей среды Красноярского края на основе мониторинговых данных // Мониторинг. Наука и безопасность, 2013. — № 3. — Вып. 11. — С. 66-83. - Пенькова Т. Г., Коробко А. В., Ничепорчук В. В., Михалев А. С.
The Integral OLAP-Model of the Emergency Risk Estimation in the Case of Krasnoyarsk Region // Proc. 36-th Int. Convention. The conf. «Business Intelligence Systems (miproBIS)», 2013. — P. 1456–146 1.
(Отдел прикладной информатики)
| К началу | |
Проект РФФИ
Руководитель: к.ф.-м.н. И. И. Рыжков
Монография посвящена теоретическому исследованию процессов тепломассообмена в бинарных и многокомпонентных смесях с учетом термодиффузии. Изучаются групповые свойства уравнений движения, проводится классификация инвариантных решений, их построение и анализ. Рассматриваются вопросы устойчивости механического равновесия и стационарного движения многокомпонентных смесей в слоях. Значительная часть работы посвящена изучению разделения многокомпонентных смесей в термодиффузионной колонне. Кроме того, рассматриваются вопросы о движении бинарных смесей под действием вибрации. Книга будет полезной научным и инженерно-техническим работникам, занимающимся тепломассообменом в смесях, измерением коэффициентов переноса, гидродинамической устойчивостью, а также групповым анализом дифференциальных уравнений. Результаты монографии также будут интересны преподавателям, аспирантам, магистрантам и студентам старших курсов вузов.
Объем монографии 200 с., 10.2 учетно-издательских листов. Монография опубликована в издательстве СО РАН тиражом в 250 экз.
Основные публикации:
- Рыжков И. И.
Термодиффузия в смесях: уравнения, симметрии, решения и их устойчивость. — Новосибирск: СО РАН, 2013. — 200 с.
(Отдел дифференциальных уравнений механики)
| К началу | |
Проект РФФИ
Руководитель: к.б.н. А. П. Толомеев (ИБФ СО РАН)
Ответственный исполнитель от ИВМ СО РАН: к.ф.-м.н. Л. А. Компаниец
В рамках трехмерной модели течения неоднородной жидкости проведены расчеты, объясняющие механизм появления внутренних волн в стратифицированном озере. Проведено длительное измерение скорости течения в точке прибрежной зоны приборами ADCP, показавшее наличие существенных горизонтальных циркуляций на дне.
Основные публикации:
- Компаниец Л. А., Якубайлик Т. В.
Численное моделирование поведения внутренних волн в прибрежной зоне неглубокого стратифицированного водоема // Сб. науч. тр. по материалам междунар. науч.-практ. конф. «Теоретические и прикладные вопросы науки и образования». — Тамбов: «ТРОО», 2013. — С. 54-58.
(Отдел Вычислительных моделей в гидрофизике)
| К началу | |
Проект РФФИ
Руководитель: д.ф.-м.н. В. Н. Гребенев (ИВТ СО РАН)
Ответственный исполнитель от ИВМ СО РАН: д.ф.-м.н., профессор О. В. Капцов
Изучалась локальная алгебра формальных дифференциальных рядов, зависящих от произвольного конечного числа переменных. Введено новое понятие пассивного множества, являющееся аналогом инволютивной системы нелинейных уравнений с частными производными. Получены достаточные условия пассивности множества. Доказательство основного утверждения принципиально отличается от аналогичного доказательства для дифференциальных уравнений.
Основные публикации:
- Kaptsov O. V.
Passive collections of differential power series algebra// arXiv.org / arXiv:1309.6587 [math.RA]. Режим доступа: http://arxiv.org/abs/1309.6587, свободный. Загл. с экрана (дата обращения: 25.10.2013).
(Отдел Вычислительных моделей в гидрофизике)
| К началу | |
Проект РФФИ
Руководитель: д.ф.-м.н., профессор Г. Г. Черных (ИВТ СО РАН)
Исполнители от ИВМ СО РАН: д.ф.-м.н., профессор О. В. Капцов, к.ф.-м.н. А. В. Шмидт
Исследовалось автомодельное вырождение течения в турбулентной круглой затопленной струе на основе полуэмпирической модели турбулентности, включающей дифференциальные уравнения переноса нормальных компонент тензора рейнольдсовых напряжений и неравновесные аппроксимации Роди для касательных напряжений. Выполнен теоретико-групповой анализ модели, построено автомодельное решение задачи.
Основные публикации:
- Шмидт А. В.
Об автомодельных решениях задачи осесимметричной турбулентной струи // Тез. докл. междунар. конф «Алгебра и Логика: Теория и Приложения». — Красноярск, 2013. — C. 151–152 .
(Отдел Вычислительных моделей в гидрофизике)
| К началу | |