| ИВМ СО РАН | Поиск |
| Отчеты ИВМ СО РАН |
Отчет ИВМ СО РАН за 2007 год
Важнейшие научные достижения 2007 года
- Важнейшие научные достижения 2007 года
- Колебания и неустойчивость токового слоя магнитосферного хвоста при наличии градиента нормальной компоненты магнитного поля
- Параллельные вычисления в задачах динамики упругопластических и сыпучих сред
- Динамическая робастность биологических сетей
- Модель связи относительного содержания хлорофилла фитопланктона с его биомассой и размерной структурой
- Уединенные волны на пленке, движимой потоком газа
- Новые аддитивные методы решения жестких задач
Колебания и неустойчивость токового слоя магнитосферного хвоста при наличии градиента нормальной компоненты магнитного поля
Авторы результата: Н. В. Еркаев, в.н.с., д.ф.-м.н., профессор; В. С. Семенов, в.н.с., д.ф.-м.н., профессор, С.-Пт. ГУ.
Исследован новый вид магнитогидродинамической неустойчивости и волны в токовом слое хвоста магнитосферы Земли, фрагмент конфигурации которого показан на рис. 1. Эти волны и неустойчивости связаны с существованием градиентов тангенциальной и нормальной, по отношению к токовому слою, компонент магнитного поля. Токовый слой может быть устойчивым или неустойчивым в зависимости от знака произведения этих градиентов. На рис. 2 показаны устойчивая (а) и неустойчивая (b) конфигурации магнитных силовых линий магнитосферного хвоста Земли при положительном и отрицательном значениях градиента нормальной компоненты магнитного поля Bz. При малом смещении δz магнитной силовой трубки из положения равновесия возникает сила F, возвращающая трубку к равновесию в случае (а) и удаляющая ее от равновесия в случае (б). Волны в области устойчивости распространяются перпендикулярно плоскостям магнитных силовых линий. Они могут быть интерпретированы как «флэпинг» волны, наблюдаемые в хвосте магнитосферы. Групповая скорость этих волн составляет несколько десятков километров в секунду, что хорошо соответствует результатам наблюдений в токовом слое хвоста магнитосферы Земли.
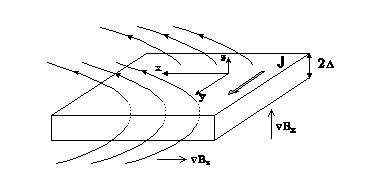
Рис. 1. Фрагмент токового слоя, пересекаемого магнитными силовыми линиями
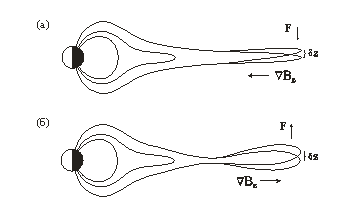
Рис. 2. Устойчивая (а) и неустойчивая (b) конфигурации магнитных силовых линий магнитосферного хвоста Земли при положительном и отрицательном значениях градиента нормальной компоненты магнитного поля Bz
| К началу | |
Параллельные вычисления в задачах динамики упругопластических и сыпучих сред
Авторы результата: В. М. Садовский, зав.отделом, д.ф.-м.н., профессор; О. В. Садовская, н.с., к.ф.-м.н.
Реологический метод построения определяющих соотношений механики деформируемого твердого тела дополнен новым элементом — жестким контактом — имитирующим поведение идеально сыпучей среды с абсолютно жесткими частицами. Это расширило область его применения, поскольку, комбинируя жесткий контакт с традиционными элементами (упругой пружиной, вязким демпфером и пластическим шарниром), можно строить реологические схемы произвольного уровня сложности для материалов, по-разному сопротивляющихся растяжению и сжатию. С помощью этого метода получены математические модели напряженно-деформированного состояния сыпучих сред, обладающих пластическими свойствами. Разработаны параллельные алгоритмы численной реализации моделей. Создан комплекс прикладных программ для исследования в пространственной постановке распространения упругопластических волн в массивах сыпучей среды, составленных из произвольного числа разнородных блоков с криволинейными поверхностями раздела. Выполнены расчеты отраженных волн в плотном грунте с жестким включением (горной породой), вызванных действием сосредоточенной импульсной нагрузки на поверхности массива (рис. 3).
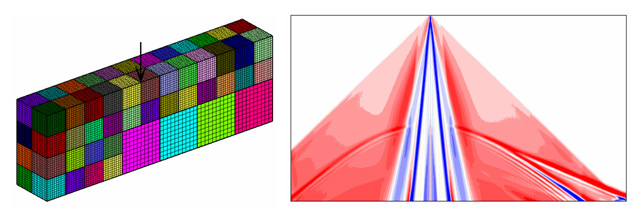
Рис. 3. Схема нагружения массива с разбиением области между вычислительными узлами и сейсмограмма отраженных волн (результаты расчетов на 68 процессорах МВС-15000)
| К началу | |
Динамическая робастность биологических сетей
Авторы результата: А. Н. Горбань, г.н.с., д.ф.-м.н., профессор; А. Ю. Зиновьев, н.с., к.т.н.
Разработана концепция распределенной робастности и r-робастности для динамических характеристик генетических и сигнальных сетей. Доказано, что для больших линейных систем с иерархическим распределением временных шкал дисперсия обратного времени релаксации много меньше, чем дисперсия индивидуальных констант (рис. 4). Более того, дисперсия обратного времени релаксации стремится к нулю быстрее, чем 1/n, где n — количество реакций. Описаны подобные явления для нелинейных систем с учетом сингулярностей времен релаксации, которые возникают вблизи точек бифуркации. Проведены исследования нелинейных моделей сигнальных сетей для важного фактора транскрипции NFkB (рис. 5).
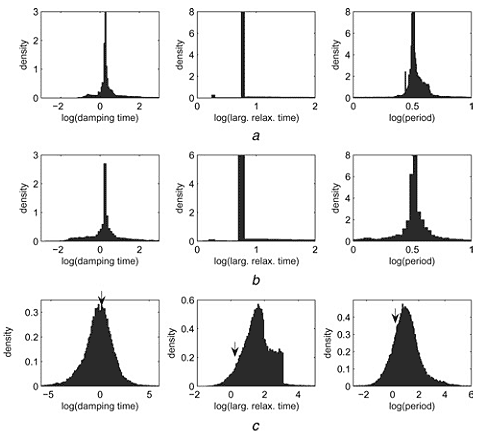
Рис. 4. Распределение характерных времен для логарифмически равномерного распределения (между 0.1 и 10) независимых шкалирующих множителей, меняющих кинетические параметры в сигнальной сети NFkB. Значение характеристики для невозмущенной системы показано стрелкой: а) шкалируется один случайно выбранный параметр; b) шкалируются два случайно выбранных параметра; c) шкалируются все параметры
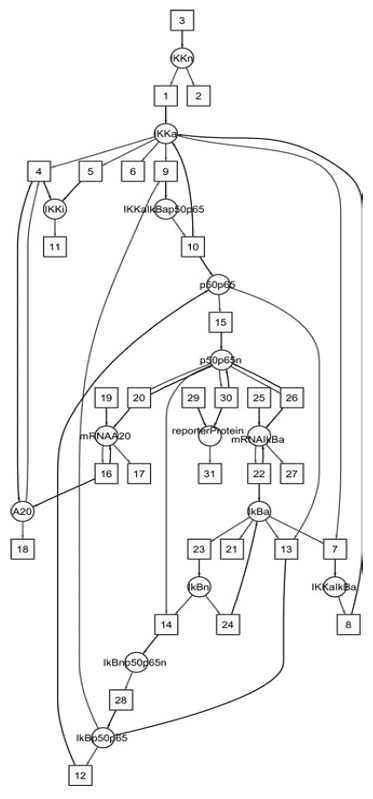
Рис. 5. Схема модели NFkB сигнальной сети
| К началу | |
Модель связи относительного содержания хлорофилла фитопланктона с его биомассой и размерной структурой
Авторы результата: А. Д. Апонасенко, в.н.с., д.ф.-м.н.; Л. А. Щур, с.н.с., д.б.н.; В. Н. Лопатин, в.н.с., д.ф.-м.н., профессор.
Разработана модель связи относительного содержания хлорофилла (β) с биомассой (Β) и дисперсной структурой сообществ фитопланктона. Зависимость для усредненных величин β и Β выражается дробно-рациональной функцией β = (0.47 + 0.088Β) / (0.037 + Β) (рис. 6) при коэффициенте корреляции r = 0.98 (общее число проб — 470). Из модели следует, что при изменениях биомассы фитопланктона величина β может изменяться в пределах от 12.5% (при Β → 0) до ≈ 0.09% при больших величинах биомассы.
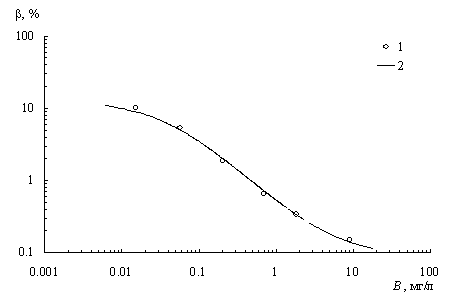
Рис. 6. Зависимость относительного содержания хлорофилла от биомассы фитопланктона: 1 — измеренные усредненные величины, 2 — аппроксимация
Полученная зависимость между β и Β обусловлена тем, что Β является в первом приближении структурным параметром, отражающим размерное распределение клеток водорослей, которое аппроксимируется степенной зависимостью Vкл = 499Β0.54 между средним объемом клетки и величиной биомассы с коэффициентом корреляции r = 0.98. При этом между β и Vкл также наблюдается связь β = 33.8Vкл−0.69 (r = 0.74), из которой следует, что мелкие клетки содержат больше хлорофилла на единицу биомассы.
Таким образом, оценку биомассы фитопланктона по содержанию хлорофилла можно проводить только в тех частных случаях, когда характеристики размерного распределения водорослей существенно не изменяются. Это особенно важно учитывать в расчетах полей фитопланктона и его продуктивности по данным дистанционного зондирования.
| К началу | |
Уединенные волны на пленке, движимой потоком газа
Автор результата: А. М. Франк, г.н.с., д.ф.-м.н., профессор.
Нелинейные волны на границе пленки, движимой потоком газа, изучены гораздо слабее их гравитационных аналогов. Немногочисленные теоретические и численные исследования имеют дело, как правило, с жидкостями с близкими плотностями и/или вязкостями, поскольку большое отличие этих величин привносит дополнительные сложности. В существующих экспериментальных работах, в отличие от экспериментов по гравитационным волнам, изучались только естественные волны, которые быстро становятся трехмерными и нерегулярными. Приводимые ниже результаты получены численно впервые.
Разработан метод частиц, на основе которого проведены численные эксперименты по изучению формирования и эволюции нелинейных волн на границе раздела. Показано существование уединенных волн в такой системе и проведено их сравнение с гравитационно-капиллярными волнами (рис. 7). Оказалось, что в канале, имеющем высоту, намного большую толщины пленки, при одинаковом числе Рейнольдса пленки эти волны имеют значительно большую амплитуду, чем гравитационно-капиллярные, а при одинаковой амплитуде — значительно меньшую фазовую скорость. При определенном масштабировании получена универсальная зависимость фазовой скорости волн на границе сдвигового течения от амплитуды.
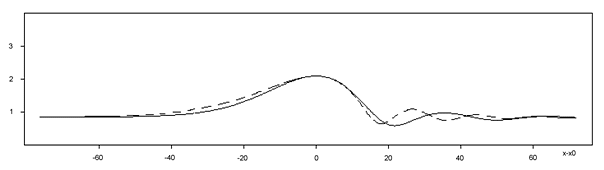
Рис. 7. Сравнение формы уединенной волны на границе раздела в сдвиговом двухфазном потоке (сплошная кривая) с гравитационно-капиллярным солитоном (пунктир) той же амплитуды
Амплитуды волн существенно зависят от относительной плотности и вязкости газа при постоянном расходе пленочного течения несмотря на то, что касательное напряжение на границе раздела для невозмущенного течения пленки не зависит от этих параметров. Высота канала существенно влияет на параметры волн, в частности, в узком канале амплитуда волн уменьшается (при фиксированном расходе в пленке), а их фазовая скорость увеличивается (при фиксированной амплитуде волн). Существует диапазон изменения расхода газа (и, соответственно, расхода жидкости), когда амплитуда стационарных волн практически не меняется, но при этом изменяется их форма и фазовая скорость (рис. 8). Таким образом, в некоторых случаях фазовая скорость волн не является однозначной функцией их амплитуды (рис. 9).
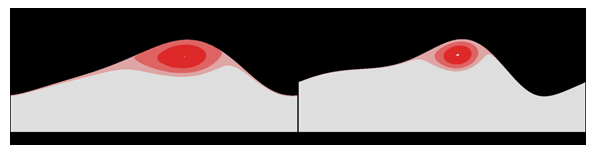
Рис. 8. Волны одинаковой амплитуды, имеющие разную форму и фазовую скорость
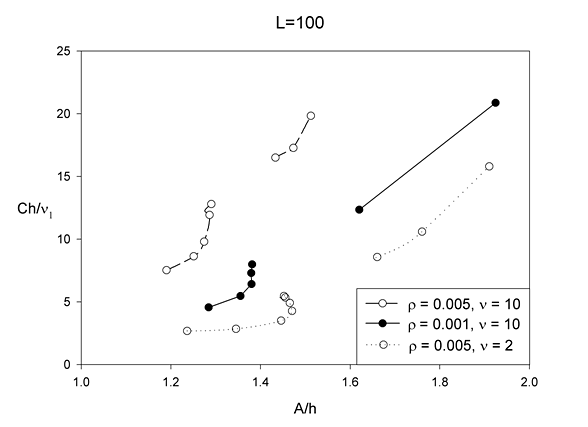
Рис. 9. Фазовая скорость волн в зависимости от амплитуды для нескольких пар газ/жидкость
| К началу | |
Новые аддитивные методы решения жестких задач
Автор результата: Е. А. Новиков, г.н.с., д.ф.-м.н., профессор.
Разработаны и исследованы новые три семейства методов решения жестких автономных и два семейства методов решения жестких неавтономных задач. Получены коэффициенты пяти L-устойчивых шестистадийных численных схем третьего порядка точности. Построены оценки ошибки и неравенства для контроля точности вычислений и устойчивости численных схем, позволяющие проводить расчеты с переменным шагом интегрирования. Проведены численные исследования построенных методов с диагональной аппроксимацией матрицы Якоби, подтверждающие их работоспособность и демонстрирующие повышение эффективности на жестких задачах более чем в 100 раз по сравнению с известными явными методами.
| К началу | |