| ИВМ СО РАН | Поиск |
| Отчеты ИВМ СО РАН |
Отчет ИВМ СО РАН за 2007 год
Программы фундаментальных исследований Сибирского отделения РАН
Механика, энергетика
Направление 3.5 «Общая механика, динамика космических тел, транспортных средств и управляемых аппаратов; биомеханика; механика жидкости, газа и плазмы, неидеальных и многофазных сред; механика горения, детонации и взрыва»
Программа 3.5.1 «Построение и анализ новых математических моделей движения сложных сред»
Координатор программы: ак. РАН Л. В. Овсянников
Проект № 3.5.1.3 «Математическое и компьютерное моделирование движения сложных сред с поверхностями раздела»№ гос. регистрации 01.2.007 09438
Научный руководитель проекта: д.ф.-м.н., проф. В. К. Андреев
Блок 1: Исследование устойчивости равновесных состояний и движений плоских слоёв с поверхностями раздела в неклассических моделях конвекции.
Исследована конвективная устойчивость равновесия в системе двух несмешивающихся жидкостей с общей границей раздела (плотности жидкостей линейно зависят от температуры и давления). Нижняя граница системы — неподвижная твердая стенка, верхняя — недеформируемая свободная поверхность. В уравнении энергии в каждой из областей учитывается функция теплового источника. На свободной границе для функции температуры заданы граничные условия третьего рода k∂θ/∂n + b(θ − θgas) = Q, где Q — полный поток тепла, Q = σR + Fi + Ft, Fi — потери тепла на испарение, Ft — потери тепла на конвективный теплообмен вода-воздух. Найдено решение, описывающее состояние механического равновесия системы двух слабо сжимаемых жидкостей. Показано, что состояние механического равновесия является неустойчивым.
Задача о возникновении конвекции в этой системе рассмотрена в применении к озеру Байкал.
Вычисления проводились для различных зон Байкала, с учетом характерных значений физических параметров (поток тепла, глубина и др.). Полученные результаты показывают, что чем меньше толщина верхнего слоя, тем активнее термодинамические процессы, протекающие в нем, и это оказывает дестабилизирующее влияние на равновесное состояние.
Построены нейтральные кривые для различных значений числа Био Bi, характеризующего интенсивность теплообмена с окружающей средой. Найдены критические числа Релея.
Из расчетов следует, что при уменьшении числа Био критические числа Релея убывают, а область неустойчивости смещается в сторону длинных волн. Полученные результаты позволяют говорить о стабилизирующем влиянии теплообмена на свободной границе.
Было проведено сравнение полученного решения с решением аналогичной задачи для слоя жидкости толщины l. В двухслойной системе неустойчивость наступает при меньших волновых числах.
Исследована устойчивость равновесного состояния двух бинарных смесей с общей поверхностью раздела в модели термодиффузии. Определяющими параметрами данной задачи являются число Марангони, число Соре и число Вебера.
Проведенные расчеты показали, что при увеличении термокапиллярного воздействия на границе раздела устойчивость равновесного состояния понижается, а рост числа Соре приводит к стабилизации границы раздела.
Исследована устойчивость конвективного течения в вертикальном слое многокомпонентной жидкости. Данная конфигурация соответствует термодиффузионной колонне (экспериментальная установка для измерения коэффициентов термодиффузии) на начальном этапе разделения смеси. В длинноволновом приближении проведен анализ устойчивости системы в широком диапазоне параметров. Проведены расчеты нейтральных кривых методом пошагового интегрирования с ортогонализацией и описаны механизмы неустойчивости. Предложена математическая модель для анализа относительной устойчивости различных конфигураций.
Блок 2: Построение на основе метода симметрий точных решений уравнений: движения смесей с учётом эффектов Соре и Дюфура, стационарных моделей турбулентности.
Групповые свойства уравнений конвекции бинарной смеси с учетом эффекта Соре обобщены на случай многокомпонентной смеси. Построено точное решение, описывающее разделение смеси в термодиффузионной колонне. Найдены преобразования эквивалентности уравнений, которые позволяют: а) исключить члены, характеризующие эффект Соре; б) исключить члены, описывающие перекрестную диффузию. Показано, что граничные условия широкого класса задач инвариантны относительно последнего преобразования. Это позволяет сводить задачи о конвекции в многокомпонентной смеси к задачам с диагональной матрицей диффузии.
Решена задача групповой классификации системы уравнений плоского турбулентного нестационарного пограничного слоя относительно функции турбулентного трения τ = g(y, uy): найдено ядро основных алгебр Ли при произвольном значении функции g и её специализации, при которых ядро основных алгебр расширяется; вычислены преобразования эквивалентности системы. Получено 12 расширений ядра основных алгебр Ли, причём специализации функции g представляют собой линейные или произвольные зависимости от uy, а также степенные и экспоненциальные зависимости от y. Показано, что в турбулентном пограничном слое продольная и поперечная компоненты скорости возрастают гораздо медленнее, чем в ламинарном слое. При этом продольная составляющая скорости асимптотически приближается к прямой, а продольная компонента на внешнем крае отлична от нуля, то есть пограничный слой, не искажая распределение продольной скорости во внешнем потоке, создает в нем поперечные токи, объяснимые трением жидкости о поверхность тела. Что касается касательного напряжения, то в ламинарном слое оно быстрее достигает своего нулевого значения, т. е. турбулентное перемешивание приводит к увеличению трения. Толщина турбулентного пограничного слоя также резко увеличивается по сравнению с толщиной ламинарного.
Решена задача групповой классификации системы уравнений конвекции несжимаемой бинарной смеси относительно функции, учитывающей силы плавучести вдоль оси z. Эта функция R(p, T, c) определяет плотность среды и зависит от давления, температуры и концентрации легких компонент в жидкости. Получена основная группа преобразований зависимых и независимых переменных системы при произвольном выборе функции R(p, T, c). Базис ядра состоит из восьми операторов. Выделены и изучены три случая: 1) функция R(p, T, c) не зависит от давления p; 2) функция R = p + Φ(T, c) — линейная по p; 3) функция R — нелинейная по p. Результаты представлены в виде таблицы групповой классификации со специализациями функции R(p, T, c) и базисами допустимых операторов.
Блок 3: Проведение группового анализа и построение инвариантных решений k-e модели турбулентности в приближении пограничного слоя.
Построены и исследованы автомодельные решения хорошо известной u'v' − k − ε модели, используемой для расчета характеристик дальнего турбулентного следа за плоским или осесимметричным телом. Найден первый интеграл редуцированной системы обыкновенных дифференциальных уравнений, что позволило уменьшить число входных данных. Полученные решения качественно и количественно хорошо согласуются с экспериментальными данными.
Найдены точные решения двухкомпонентных систем уравнений реакция-диффузия с помощью метода линейных определяющих уравнений (ЛОУ), обобщающего методы классического группового анализа дифференциальных уравнений. Проведено построение ЛОУ для системы двух эволюционных уравнений второго порядка. Представлены результаты решения ЛОУ для двухкомпонентных систем реакция-диффузия со степенными нелинейностями в коэффициентах диффузии. Приведены примеры построения неинвариантных решений для систем реакция-диффузия, обладающих найденными инвариантными многообразиями.
Построены линейные определяющие уравнения для системы двух эволюционных уравнений второго порядка. Проведено решение линейных определяющих уравнений для двухкомпонентных систем реакция-диффузия со степенными нелинейностями в коэффициентах диффузии, что позволило построить ряд неинвариантных точных решений соответствующих систем.
Блок 4: Разработка численного алгоритма для определения вертикальных распределений гидрофизических и гидробиологических характеристик слабопроточного водоема. Модифицирование методики для исследования годового температурного режима соленого озера с учетом динамики ледяного покрова. Разработка численных алгоритмов для определения вертикальных распределений гидробиологических характеристик в зимний период и для определения гидрофизических и гидробиологических переменных на грубых в горизонтальном направлении сетках.
Выполнена модификация одномерной в вертикальном направлении математической модели температурного и солевого режимов озера с учетом ледообразования. Предложены упрощенные модели для определения динамики толщины ледяного покрова и оценки толщины слоя конвективного перемешивания воды. В весенний период моделируются процессы таяния льда как с нижней поверхности ледяного покрова, так и с верхней. В период отсутствия ледяного покрова ветровое воздействие учитывается при параметризации коэффициента вертикального турбулентного обмена.
Предложена методика для определения вертикальных распределений гидробиологических характеристик водоема под ледяным покровом. После определения толщины слоя конвективного перемешивания решаются уравнения переноса и диффузии относительно гидробиологических характеристик со специальной параметризацией коэффициента вертикального обмена; в слое конвективного перемешивания коэффициент берется достаточно большим, а ниже этого слоя равен минимальному значению.
Предложен вычислительный алгоритм для определения гидрофизических и гидробиологических переменных на грубых в горизонтальном направлении сетках. На рис. 24 приведены вертикальные профили температуры, рассчитанные на подробной 100х40 и грубой 22х40 в горизонтальном направлении сетках. Хорошее совпадение результатов расчетов позволяет рекомендовать разработанный алгоритм для исследования вертикальной структуры водоема с использованием грубых в горизонтальном направлении сеток.
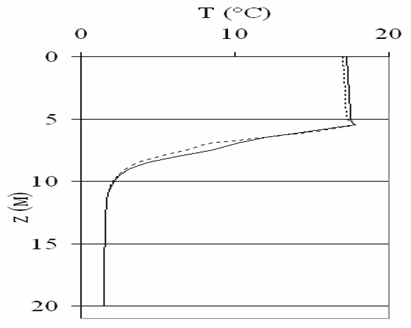
Рис. 24. Вертикальные профили температуры в глубоководной зоне озера Шира. Результаты расчетов: на сетке 100х40 — сплошная линия, на сетке 22х40 — пунктирная линия
Блок 5: Изучение закономерностей образования и параметров нелинейных волн в пленке, движимой потоком газа в плоском канале.
Проведено численное исследование стационарных нелинейных волн на поверхности жидкой пленки, движимой потоком газа в мини-канале. Изучалось влияние высоты канала (относительно толщины пленки) и физических свойств пары газ/жидкость на параметры волн. В частности показано, что:
- расход пленочного течения с волнами на границе раздела зависит от плотности газа, в отличие от плоского течения пленки с невозмущенной границей;
- амплитуды волн существенно зависят от плотности и вязкости газа, даже при постоянном расходе пленочного течения (несмотря на то, что касательное напряжение на границе раздела для невозмущенного течении пленки не зависит от этих параметров);
- высота канала существенно влияет на параметры волн, в частности, в узком канале амплитуда волн уменьшается (при фиксированном расходе в пленке), а их фазовая скорость увеличивается (при фиксированной амплитуде волн);
- существует диапазон изменения расхода газа (и, соответственно, расхода жидкости), когда амплитуда стационарных волн практически не меняется. При этом изменяется их форма и фазовая скорость. Таким образом, фазовая скорость волн не является однозначной функцией их амплитуды;
- автомодельность профилей продольной скорости, известная для гравитационно-капиллярных волн не слишком большой амплитуды, имеет место и для волн, движимых потоком газа. При этом в узком канале она нарушается для волн существенно меньшей амплитуды, чем в широком.
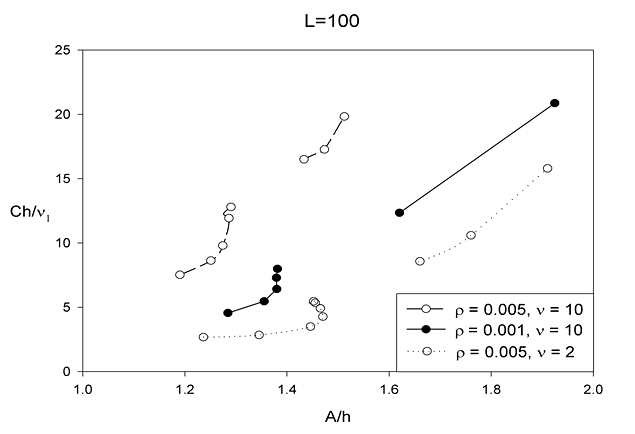
Рис. 25. Фазовая скорость волн в зависимости от амплитуды для нескольких пар газ/жидкость
Основные публикации.
К блоку 1:
- Андреев В. К., Картошкина А. Е.
Автомодельное движение бинарных смесей с плоской границей раздела // Сибирский журнал индустриальной математики. — 2007. — Т. 10. — № 1(29). — С. 17-24. - Андреев В. К., Бекежанова В. Б.
Конвективная неустойчивость системы горизонтальных слоёв слабосжимаемых жидкостей // ПМТФ. — 2007. — Т. 48. — № 4. — С. 15-22. - Андреев В. К.
Нестационарное движение плоских слоёв вязких жидкостей с общей границей раздела // Вычислительные технологии. — 2007. — Т. 12. — № 5. — С. 23-30. - Бекежанова В. Б.
Исследование устойчивости равновесного состояния в модели конвекции с нелинейной зависимостью плотности от температуры и давления // ПМТФ. — 2007. — Т. 48. — № 2. — С. 66-74. - Ryzhkov I. I. and Shevtsova V. M.
On thermal diffusion and convection in multicomponent mixtures with application to the thermogravitational column // Physics of Fluids. — 2007. — Vol. 19. — Is. 2. — 027101 (17 р). - Ефимова М. В.
Неустойчивость поверхности раздела равновесного состояния двух бинарных смесей с учетом эффекта Соре // Вычислительные технологии. — 2007. — Т. 12. — № 6. — С. 18-30.
К блоку 2:
- Ефимова М. В.
Эволюция возмущений движения бинарных смесей с плоской границей раздела под действием перепада давления и термоконцентрационных сил // Препринт № 4. — Красноярск: ИВМ СО РАН. — 2007. — 40 с. - Степанова И. В.
Инвариантная подмодель уравнений турбулентного пограничного слоя // Материалы конф. молодых ученых ИВМ СО РАН. — Красноярск: ИВМ СО РАН. — 2007. — С. 30-36. - Андреев В. К.
Стабилизация решений краевой задачи о совместном движении двух бинарных смесей // Тез. докл. междунар. конф. «Дифференциальные уравнения, теория функции и приложения». — Новосибирск: НГУ. — 2007. — С. 63-64. - Родионов А. А.
Групповая классификация уравнений одной модели конвекции // Тез. докл. междунар. конф. «Дифференциальные уравнения, теория функции и приложения». — Новосибирск: НГУ. — 2007. — С. 267.
К блоку 3:
- Шмидт А. В.
Анализ систем реакция-диффузия методом линейных определяющих уравнений // ЖВМиМФ. — 2007. — Т. 47. — № 2. — С. 253–265 . - Капцов О. В., Ефремов И. А., Шмидт А. В.
Инвариантные решения модели турбулентности // Тез. междунар. конф. «Потоки и структуры в жидкостях». — Ст.-Петербург. — 2007. — С. 240–241 . - Капцов О. В.
Инвариантные функции и тензоры уравнений гидродинамики // Тез. всерос. конф. «Проблемы механики сплошных сред и физики взрыва». -Новосибирск. — 2007. — С. 98.
К блоку 4:
- Белолипецкий П. В.
Комплекс компьютерных программ для исследования гидробиологических и гидрофизических процессов в озерах // Материалы конф. молодых ученых ИВМ СО РАН. — Красноярск: ИВМ СО РАН. — 2007. — С. 4-9.
К блоку 5:
- Frank A. M.
The influence of gas-liquid properties on gas driven waves in a film // Microgravity sci. technol. — 2007. — Vol. XIX. — Is. 3-4. — Р. 38-40.
(Отделы вычислительных моделей в гидрофизике, дифференциальных уравнений механики)
| К началу | |
Направление 3.6 «Механика твердого тела, физика и механика деформирования и разрушения, механика композиционных и наноматериалов, трибология»
Программа 3.6.3 «Механика деформирования и разрушения однородных и композитных материалов и конструкций для транспортных и авиационных систем»
Координатор программы: чл.-корр. РАН Б. Д. Аннин
Проект № 3.6.3.3 «Разработка вероятностных моделей предельных состояний, ресурса и живучести материалов и конструкций технических систем для оценки показателей техногенного риска»№ гос. регистрации 01.2.007 09436
Научный руководитель проекта: д.т.н., проф. В. В. Москвичев
Структурная неоднородность является одним из характерных признаков современных конструкционных материалов и конструкций. Поэтому анализ предельных состояний и разрушений с учетом структурной неоднородности представляет особый интерес для оценки безопасного ресурса и живучести конструкций в аварийных ситуациях.
В ходе исследований получены следующие результаты. Разработаны модели и расчетно-экспериментальные методы оценки предельных состояний и вероятностей разрушения конструкций из структурно-неоднородных материалов. Сформулированы и разработаны основные положения концепции живучести в задачах проектирования и эксплуатации конструкций технических систем. Отличительные особенности концепции состоят в комплексном учете физико-механических свойств конструкционных материалов, структурно-механической неоднородности, конструктивных форм, структурной избыточности и резервирования элементов конструкций. Реализация концепции базируется на исследованиях технологической и эксплуатационной дефектности, компонент номинальных и локальных напряжений и деформаций, кинетических уравнений роста трещин и деградации свойств материалов, предпосылок, факторов и механизмов формирования аварийных ситуаций. Концепция включает обоснование и формулировку системы показателей живучести, установление взаимосвязи показателей прочности, надежности и живучести, количественную расчетно-экспериментальную оценку живучести, методы обеспечения живучести на стадиях проектирования и эксплуатации конструкций. Концепция позволяет решать задачи сравнительного многовариантного анализа конструктивного исполнения и конструктивных форм элементов и конструкций, проектный анализ сценариев аварийных ситуаций, оценку запасов прочности и остаточного ресурса конструкций, восстановление сценариев аварийных ситуаций для произошедших аварий технических систем.
На основе разработанных подходов и моделей выполнен анализ предельных состояний и живучести конструкций ряда технических систем. В частности, рассмотрены особенности напряженного-деформированного состояния и определены характеристики живучести сосудов давления. Выявлены наиболее характерные потенциальные зоны разрушений ресиверов и ректификационных колонн опасных производственных объектов, исследованы особенности напряженно-деформированного состояния таких зон с оценкой коэффициентов концентрации напряжений и коэффициентов запаса прочности для заданного критерия предельного состояния (рис. 26).
Проведен анализ напряженно-деформированного состояния конструкций рам карьерных автосамосвалов. Выявлены основные причины и закономерности образования трещин в процессе эксплуатации, установлены особенности перераспределения напряжений в области конструктивных концентраторов и эксплуатационных повреждений в виде трещин.
Выполнен анализ особенностей напряженно-деформированного состояния корпуса верхнего оголовка несущей стрелы стартового комплекса запуска ракет. Определены компоненты напряжений и деформаций корпуса оголовка при заданных расчетных (проектных) и аварийных нагрузках (рис. 27). Установлено, что при некоторых сочетаниях проектных нагрузок, а также при возникновении аварийных перегрузок не обеспечиваются требуемые коэффициенты запаса прочности конструкции (рис. 28).
Разработана вероятностная модель, позволяющая оценить резервирующую способность (способность системы сопротивляться разрушению при наличии полностью или частично поврежденных элементов) систем с параллельным соединением несущих элементов. Определены условия, при которых отказ отдельных элементов не приводит к катастрофическому разрушению всей системы. Критическое число отказавших элементов оценивается по параметрам распределения их прочности и общего числа элементов системы. Показано, что при увеличении числа несущих элементов снижается среднее значение напряжений, приводящих к разрушению отдельного элемента, но возрастает уровень напряжений, при котором происходит катастрофическое разрушение всей системы, за счет увеличения резервирующей способности.
На основе структурно-имитационной модели волокнистого композиционного материала, учитывающей статистическую природу прочности компонентов, выполнены расчеты по определению зависимости разрушающих напряжений от размера начального трещиноподобного дефекта, перпендикулярного направлению армирования, для материала углеродные волокна/эпоксидная матрица. Анализ результатов показывает, что при увеличении длины трещины значения разрушающих напряжений не проявляют асимптотического снижения, характерного для однородных материалов. Это обусловлено формированием в области перед вершиной трещины зоны локальных разрушений (обрывы волокон, разрушение или пластическое деформирование матрицы, разрушение границы волокно/матрица), что приводит к снижению уровня концентрации напряжений. В отличие от гомогенных материалов такая зона более развита в направлении, перпендикулярном плоскости трещины, за счет интенсивного расслоения по межфазовой границе (рис. 29). Таким образом, поведение композита с трещиной в основном контролируется сдвиговой прочностью границы раздела компонентов и энергоемкостью матрицы. Для неповрежденного материала также существует оптимальное значение (для фиксированного объемного содержания армирующего волокна) сдвиговой прочности межфазовой границы, при котором материал обладает максимальной вязкостью разрушения. Однако это значение отличается от оптимальной прочности границы раздела для бездефектного композита.
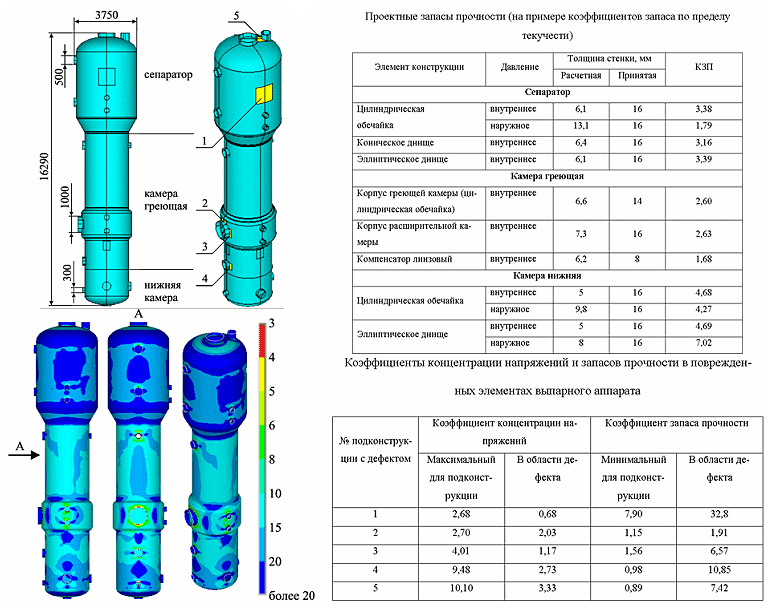
Рис. 26. Результаты расчета технологической колонны
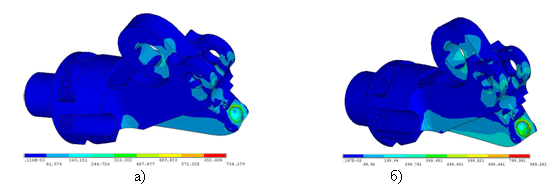
Рис. 27. Распределение интенсивности напряжений для второго расчетного случая: а) проектные нагрузки; б) фактор нагрузки k = 1,7
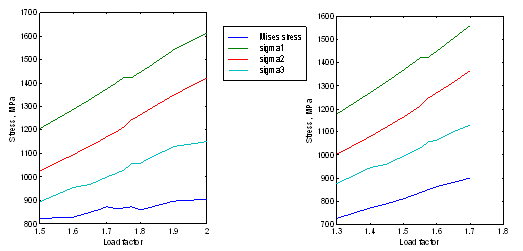
Рис. 28. Зависимость максимальных напряжений от фактора нагрузки: а) первый расчетный случай; б) второй расчетный случай
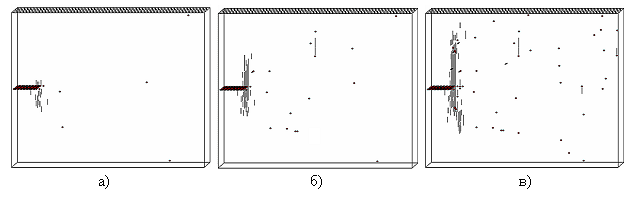
Рис. 29. Развитие зоны микроповреждений в вершине трещины в композите углеродные волокна/эпоксидная матрица (Vf = 0.3):
Основные публикации:
- Безопасность России. Правовые, социально-экономические и научно-технические системы. Анализ риска и проблемы безопасности. Прикладные вопросы анализа рисков критически важных объектов / Лепихин А. М., Москвичев В. В., Черняев А. П. / Научн. руковод. К. В. Фролов
. — М.: МГФ «Знание», 2007. — Ч. 3. — 816 с. - Доронин С. В., Москвичев В. В.
Моделирование прочности, надежности и живучести поврежденных элементов конструкций // Химическое и нефтегазовое машиностроение. — 2007. — № 1. — С. 37-42. - Доронин С. В., Шигин А. О.
Систематизация потенциально опасных конструкций технологического оборудования глиноземного производства // Безопасность труда в промышленности. — 2007. — № 1. — С. 72-75. - Доронин С. В., Сигова Е. М.
Задачи расчетного анализа оболочечных элементов технологического оборудования // Химическое и нефтегазовое машиностроение. — 2007. — № 3. — С. 3-6. - Лепихин А. М., Москвичев Е. В.
Оценка надежности сварных соединений трубопроводов, содержащих дефекты в виде непроваров // Вестник СибГАУ. — 2007. — С. 123–124 . - Лепихин А. М.
Неразрушающий контроль и оценка опасности дефектов сварки на стадии эксплуатации оборудования // Вопросы материаловедения. — 2007. — № 3 (51). — С. 208–213 .
(Отдел машиноведения)
| К началу | |