| ИВМ СО РАН | Поиск |
| Отчеты ИВМ СО РАН |
Отчет ИВМ СО РАН за 2009 год
Программы фундаментальных исследований Сибирского отделения РАН
Механика, энергетика
Направление 3.5 «Общая механика, динамика космических тел, транспортных средств и управляемых аппаратов; биомеханика; механика жидкости, газа и плазмы, неидеальных и многофазных сред; механика горения, детонации и взрыва»
Программа 3.5.1 «Построение и анализ новых математических моделей движения сложных сред»
Координатор программы: академик РАН Л. В. Овсянников
Проект № 3.5.1.3 «Математическое и компьютерное моделирование движения сложных сред с поверхностями раздела»№ гос. регистрации 01.2.007 09438
Научный руководитель проекта: д.ф.-м.н., профессор В. К. Андреев
Блок 1: Исследование устойчивости равновесных состояний и движений плоских слоёв с поверхностями раздела в неклассических моделях конвекции.
Ответственный исполнитель: д.ф.-м.н., профессор В. К. Андреев.
1.1. Методами численного моделирования для системы уравнений конвекции, полученной осреднением, исследована задача о смешивании бинарной смеси в прямоугольной области при условиях пониженной гравитации в быстроменяющемся внешнем горизонтальном силовом поле. Начальное состояние системы имеет узкую поверхность раздела двух компонентов смеси, что соответствует условию устойчивого равновесия. Задача рассматривалась применительно к водно-спиртовым растворам с учетом зависимости коэффициентов вязкости и диффузии от концентрации.
На рис. 25 представлены результаты расчетов (поле концентрации) при изменении аспектного отношения AR cторон расчетной области для случаев AR = 0.5, 1 и 2. При увеличении аспектного отношения AR наблюдается потеря устойчивости границы раздела жидкостей с проявлением ее существенной деформации и интенсивным перемешиванием компонентов смеси. Видно, что после начала вибрации потоки компонентов смеси проникают друг в друга в режиме пристеночного течения. При этом неоднородное распределение вертикальной скорости в потоке приводит к образованию неустойчивости Кельвина-Гельмгольца. С уменьшением аспектного отношения достигается обратный эффект — происходит стабилизация структуры течения, а процесс смешивания компонентов уменьшается в пределе до диффузионных порядков.
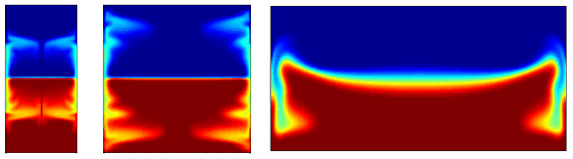
Рис. 25
Для рассматриваемой системы наличие дополнительных сил, действующих в направлении наложенных вибраций, может иметь определяющее значение в связи с потерей устойчивости границы раздела жидкостей. На рис. 26 представлены результаты расчетов влияния горизонтальной силы, которая придает ускорение a = 0.01 g0 (g0 — ускорение силы тяжести на Земле). Видно, что в случае малых аспектных отношений такое воздействие не приводит к потере устойчивости, которое наблюдается для AR = 2.
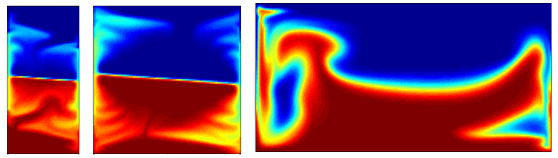
Рис. 26
1.2. Исследована устойчивость стационарного течения тонкой жидкой пленки, увлекаемой потоком газа в микроканале. Течение сред описывается уравнениями Навье-Стокса и энергии. Поверхность раздела считается деформируемой. Предполагается, что в газе реализуется течение Пуазейля и вектор скорости имеет вид v = (0,0,w(x,y)). Коэффициент поверхностного натяжения линейно зависит от температуры: σ = σ0 − kθ.
Выписаны уравнения малых возмущений стационарных течений жидкости. Численно решена спектральная задача относительно комплексного декремента, определяющего временной ход возмущения. В табл. 2 приводятся расчетные значения амплитуды деформации пленки Δh, критическая длина волны возмущений λ*, приводящих к неустойчивости, для различных значений числа Рейнольдса газа Reg и жидкости Rel и ускорения свободного падения (g0 = 9.8 м/с2). Вычисления проводились для систем вода-воздух и FC-72-азот.
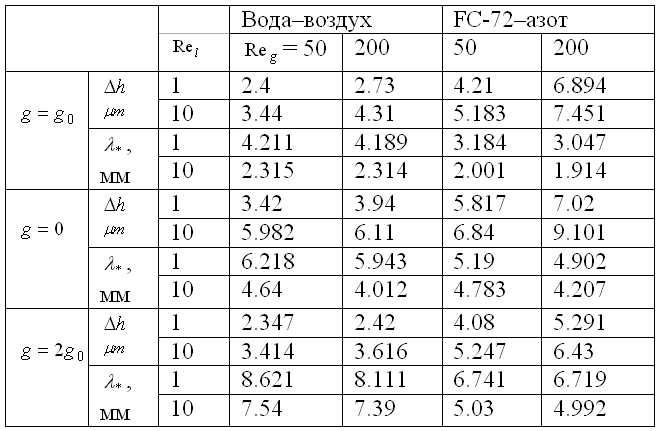
Таблица 2
Построены нейтральные кривые (рис. 27) при g = g0, где k — волновое число.
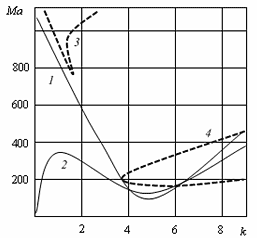
Рис. 27 Нейтральные кривые Ma(k): 1,3 — система вода-воздух, 2,4 — FC-72-азот
Нейтральные кривые колебательной неустойчивости обозначены штриховыми линиями, монотонной неустойчивости — сплошными. Области неустойчивости находятся внутри кривых. При больших числах Rel выделены 2 типа колебательной неустойчивости — капиллярная и термокапиллярная. В случае термокапиллярных волн неустойчивость порождается интенсивным течением в продольном направлении вблизи свободной поверхности. При больших расходах газа течение неустойчиво.
1.3. В рамках данного проекта, завершено исследование устойчивости стационарного конвективного течения многокомпонентной смеси в термогравитационной колонне (экспериментальной установки для измерения коэффициентов термодиффузии). В рамках линейной теории проведены расчеты критических параметров неустойчивости методом Галеркина, а также методом пошагового интегрирования с ортогонализацией. Исследовались два типа возмущений: продольные волны, распространяющиеся в вертикальном направлении, и поперечные волны, распространяющиеся перпендикулярно плоскости, образованной градиентом температуры и вертикальной осью колонны. Впервые исследована устойчивость тройных смесей в колонне, а также проведены расчеты для бинарных смесей в широкой области параметров
1.4. Рассмотрено нестационарное движение сферического слоя идеальной жидкости и его устойчивость. Показано, что эволюция внутреннего безразмерного радиуса слоя сводится к решению задачи Коши для нелинейного уравнения 2-го порядка
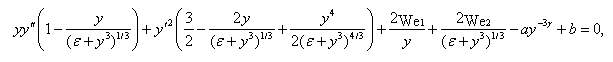
где ε > 0 характеризует начальную толщину, Wej — числа Вебера, a > 0, b > 0 характеризуют внутреннее и внешнее давления, γ — показатель адиабаты. Доказано, что уравнение имеет единственное стационарное решение yc, причем yc → 0 при b → ∞, и это решение является устойчивым.
В общем случае уравнение имеет первый интеграл энергии. С его помощью доказывается, что решение всегда периодическое. Это означает, что сферический слой совершает колебательное движение. Рассмотрена линеаризованная задача о малых возмущениях данного периодического движения. Использован метод лагранжевых координат для получения системы обыкновенных дифференциальных уравнений, описывающих эволюцию амплитуд возмущений поверхностей слоя. Установлено, что при нулевом номере сферической гармоники наблюдаются периодически повторяющиеся возмущения внутреннего и внешнего слоя, причем изменение поверхностного натяжения влияет только на период колебаний. С ростом номера гармоник и начальной толщины слоя нарастает амплитуда колебаний. Рассмотрено также влияние всех физических параметров на поведение возмущений.
Блок 2: Разработка и численное исследование дискретных моделей композитных сред на основе многосеточного моделирования и совместного применения микро- и макроподходов.
Ответственный исполнитель — д.ф.-м.н, профессор Л. И. Шкутин.
Методом пристрелки численно решены нелинейные краевые задачи о плоском изгибе упругих арок и панелей под равномерно распределенной нагрузкой. Задачи сформулированы для системы шести обыкновенных дифференциальных уравнений первого порядка с независимыми полями конечных перемещений и поворотов. Рассмотрены два варианта граничных условий: шарнирное опирание и жесткое защемление. Получены разветвленные решения краевых задач.
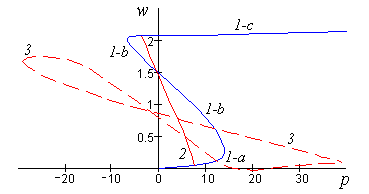
Рис. 28. Карта ветвления равновесных состояний круговой арки и цилиндрической панели при шарнирных опорах на горизонтальную плоскость: p — параметр нагрузки, w — вертикальное перемещение вершины; 1, 2 — ветви низших симметричных и несимметричных конфигураций, 3 — ветвь высших симметричных конфигураций
Множество решений включает устойчивые и неустойчивые, симметричные и несимметричные формы изгиба, соответствующие положительным, отрицательным и нулевым значениям нагрузки. По результатам расчета построены фазовые карты решений в зависимости от параметра нагрузки.
Разработаны процедуры построения почти эквивалентных дискретных моделей для пространственных упругих тел сложной формы и двухсторонних оценок для погрешностей конечноэлементных решений плоской задачи упругости. Первая проблема решается с помощью смешанных конечноэлементных моделей, которые проектируются на основе совместного применения одно- и двухсеточного моделирования. Вторая процедура сводится к выбору конечного множества двумерных изотропных однородных тел в плоском напряженном состоянии, имеющих различные размеры, условия закрепления и кусочно-равномерного нагружения, для которых известны точные решения. Для исходного тела, используя заданный закон измельчения, строится последовательность регулярных разбиений, состоящих из конечных элементов заданного порядка. Далее с помощью метода конечных элементов строится решение плоской задачи.
Блок 3: Построение на основе метода симметрий точных решений уравнений: движения смесей с учётом эффектов Соре и Дюфура, стационарных моделей турбулентности.
Ответственный исполнитель — д.ф.-м.н, профессор В. К. Андреев, д.ф.-м.н, профессор О. В. Капцов.
3.1. Решена задача групповой классификации уравнений плоского нестационарного пограничного турбулентного слоя относительно двух функций: турбулентного трения τ(y,uy) и функции, определяющей градиент давления θ(t,x). Следует отметить, что существенной особенностью этой системы уравнений является наличие тривиальной основной алгебры Ли: в ней нет ни одного оператора. Результатом решения задачи групповой классификации служит таблица, в которой представлено 15 сочетаний специализаций классифицируемых функций и перечислены операторы, допускаемые системой уравнений для каждой пары функций τ(y,uy), θ(t,x). Допускаемые операторы в основном представляют собой операторы растяжения, сдвигов и галилеевых переносов, что типично для уравнений, описывающих реальные физические процессы.
3.2. В рамках проекта была исследована модель вибрационной конвекции бинарной смеси с помощью теоретико-групповых методов. Вибрационной конвекцией называют специальные течения, которые возникают в жидкости с градиентом плотности под действием внешней вибрации. В бинарной смеси градиент плотности может быть вызван градиентами температуры и концентрации. В случае высоких частот течение можно условно разделить на две составляющие: «быструю», которая осциллирует с частотой внешнего воздействия, и «медленную», осредненную по времени часть, которая характеризует нелинейные взаимодействия в жидкости под действием периодической внешней силы.
3.3. Рассмотрена трехмерная стационарная k-ε модель в приближении дальнего турбулентного следа в пассивно стратифицированной среде. С помощью группового анализа и метода линейных определяющих уравнений найдено представление для решений, позволяющее свести исходную модель к системе обыкновенных дифференциальных уравнений. Получены решения, удовлетворяющие всем краевым условиям. Важно отметить, что данные решения не являются автомодельными, но удовлетворительно согласуются с экспериментальными данными и имеющимися расчетами полной модели.
Блок 4: Численное исследование биологических и гидрофизических механизмов формирования неоднородных распределений компонент озерных экосистем.
Ответственный исполнитель — д.ф.-м.н, профессор В. М. Белолипецкий.
Вертикальная плотностная стратификация оказывает решающее влияние на пространственно-временные распределения химических компонент и экологию планктонных организмов в глубоких озерах. В водной толще стратифицированных водоемов формируются экологически значимые вертикальные градиенты температуры, света, кислорода, солености, редокс-потенциала, биогенных элементов и других компонентов экосистемы. Вдоль градиентов физических и химических характеристик формируются различные экологические ниши планктонных микроорганизмов, что приводит к формированию устойчивых неоднородностей вертикального распределения различных видов бактерио-, фито- и протозоопланктона. Разработана одномерная вертикальная модель, описывающая годовую динамику вертикальной структуры соленого озера с учетом процессов образования и таяния льда. Предложен метод для определения вертикальных распределений гидробиологических характеристик водоема под ледяным покровом. После определения толщины слоя конвективного перемешивания решаются уравнения переноса и диффузии относительно гидробиологических характеристик со специальной параметризацией коэффициента вертикального обмена; в слое конвективного перемешивания коэффициент берется достаточно большим, а ниже этого слоя равен минимальному значению.
С помощью разработанных компьютерных моделей и использования натурных данных исследованы сезонные режимы вертикальной структуры озера Шира. Показано, что толщина слоя конвективного перемешивания под ледяным покровом в основном зависит от метеоданных в осенний период. Различные вертикальные распределения температуры, солености и плотности воды в разные годы объясняются различиями метеорологических условий.
Важными элементами вертикальной гидрофизической структуры соленого озера являются термоклин, халоклин и пикноклин, в которых наблюдаются наибольшие изменения по вертикали соответственно температуры, солености и плотности воды. Эти слои разделяют водные массы с более однородными характеристиками. Согласно натурным данным заглубления термоклина, халоклина и пикноклина для озера Шира практически совпадают и зависят от метеоданных и периода года. Из натурных данных следует, что в озере Шира положение редокс-зоны (границы раздела слоев, насыщенных кислородом и сероводородом) совпадает со «ступенькой» плотности для осеннего и зимнего сезонов. В свою очередь, положение «ступеньки» плотности, рассчитанное по гидрофизической модели согласуется с натурными данными. Летом и весной редокс-зона находится существенно ниже пикноклина. В зоне перехода от аэробных слоев водной толщи к анаэробным (редокс-зона) обычно наблюдается повышенная активность планктонных сообществ. Глубина расположения редокс-зоны является важнейшей характеристикой стратифицированного водоема.
Для летнего режима выполнена стыковка гидрофизической и биофизической моделей. Для зимнего периода биофизическая модель находится в стадии разработки.
Построенная компьютерная модель позволяет прогнозировать динамику вертикальной структуры водоема для различных сценариев изменений климата и антропогенной нагрузки. Комплекс программ передан в Институт биофизики СО РАН для исследования вертикальной структуры водной экосистемы озера Шира.
Блок 5: Исследование свойств и области применимости численной модели для капиллярных менисков с движущейся контактной линией.
Ответственный исполнитель — д.ф.-м.н, профессор А. М. Франк.
Проведено численное исследование модели для капиллярных менисков с движущейся контактной линией на примере задачи о медленном погружении жесткой пластины в вязкую жидкость. Расчеты проводились в широком диапазоне значений капиллярного числа Ca = 0.005 − 0.461. Результаты сравнивались с известными экспериментами (Garoff et al., Phys. Fluids, 7(11), 1995, 2631). Показано, что с помощью изменения времени реинициализации Tr (внутреннего параметра модели) можно получить хорошее согласие с экспериментом не только по динамическому углу контакта, но и по форме мениска во всем рассмотренном диапазоне капиллярного числа. Более того, при не слишком больших значениях Ca наблюдается численная сходимость результатов при условии пропорционального уменьшения Tr вместе с пространственным и временным шагами схемы. Тем не менее, Tr не является, к сожалению, универсальным по Ca параметром и в этом смысле предложенная модель не является пока качественным продвижением по сравнению с известными моделями, например, использующими «длину проскальзывания», которые также не дают универсального описания геометрии движущегося мениска.
Основные публикации.
К блоку 1:
- Gaponenko Y., Shevtsova V.
High frequency vibration effect on the water-isopropanol mixture // EUROTHERM, Seminar Nr. 84. — Namur, Belgium. — 2009. — 4 p. - Рыжков И. И., Шевцова В. М.
Термодиффузия и конвекция в многокомпонентных смесях: теоретическое описание и приложения // Тез. докл. всеросс. конф. «Успехи механики сплошных сред», приуроченной к 70-летию ак. В. А. Левина. — Владивосток: Дальнаука. — 2009. — С. 139. - Bekezhanova V., Kabov O.
Instability of stationary flow of liquid film driven by gas flow // Book of abstracts Third International Topical Team Workshop on «Two-Phase Systems for Ground and Space Applications». — Novosibirsk. — 2009. — P. 31. - Ryzhkov I. I., Shevtsova V. M.
Interfacial flow control in two-phase systems with application to liquid bridges // Abstracts of 62nd Annual Meeting of the APS Division of Fluid Dynamics. — 2009. AQ.00003. - Андреев В. К.
Об устойчивости колебательного движения сферического слоя идеальной жидкости // Тез. докл. всерос. конф. «Новые математические модели механики сплошных сред: построение и изучение». — Новосибирск: ИГиЛ СО РАН. — 2009. — С. 16-17.
К блоку 2:
- Матвеев А. Д.
Почти эквивалентное дискретное моделирование трехмерных пористых тел сложной формы на основе смешанных моделей // Вестник СибГАУ. — 2009. — Вып. 3(24). — C. 34-42. - Матвеев А. Д.
Процедура построения двусторонних оценок погрешностей конечноэлементных решений плоской задачи упругости // Вестник СибГАУ. — 2009. — Вып. 4(25). — C. 21-29. - Шкутин Л. И.
Анализ разветвленных форм изгиба арок и панелей // ПМТФ. — 2009. — Т. 50. — № 6. — С. 155–160 .
К блоку 3:
- Ефремов И. А., Капцов О. В., Черных Г. Г.
Симметрии и решения полуэмпирических моделей турбулентности // Сб. науч. тр. «Симметрии дифференциальных уравнений.» — М.: МФТИ. — 2009. — С. 79-88. - Капцов О. В., Шмидт А. В.
Неавтомодельные решения трехмерной полуэмпирической дальнего турбулентного следа // Тез. докл. XI Междунар. семинара «Супервычисления и математическое моделирование». — Саров: ФГУП «РФЯЦ-ВНИИЭФ». — 2009. — С. 73. - Капцов О. В., Шмидт А. В.
Решения трехмерной модели дальнего турбулентного следа // Тез. всерос. конф. «Новые математические модели механики сплошных сред: построение и изучение». — Новосибирск. — 2009. — С. 73. - Степанова И. В.
Групповые свойства уравнений двумерного турбулентного пограничного слоя при заданном давлении // Тез. докл. всерос. конф. «Новые математические модели механики сплошных сред: построение и изучение». — Новосибирск: ИГиЛ СО РАН. — 2009. — С. 134. - Степанова И. В.
Задача идентификации двух функций в системе уравнений турбулентного пограничного слоя // J. of Siberian Federal University. Mathematics and Physics. — 2009. — № 2(2). — P. 245–252 .
К блоку 4:
- Белолипецкий П. В., Белолипецкий В. М., Генова С. Н.
Численное моделирование годового режима вертикальной стратификации соленого озера Шира // Материалы Национальной конф. «Математическое моделирование в экологии». — Пущино: ИФХиБПП РАН. — 2009. — С. 34-35.
(Отделы вычислительных моделей в гидрофизике, дифференциальных уравнений механики)
| К началу | |
Направление 3.6 «Механика твердого тела, физика и механика деформирования и разрушения, механика композиционных и наноматериалов, трибология»
Программа 3.6.3 «Механика деформирования и разрушения однородных и композитных материалов и конструкций для транспортных и авиационных систем»
Координатор программы: член-корреспондент РАН Б. Д. Аннин
Проект № 3.6.3.3 «Разработка вероятностных моделей предельных состояний, ресурса и живучести материалов и конструкций технических систем для оценки показателей техногенного риска»№ гос. регистрации 01.2.007 09436
Научный руководитель проекта: д.т.н., профессор В. В. Москвичев
Основное содержание работ этапа 2009 г. состояло в проведении модельных расчетов ресурса, живучести конструкций и техногенного риска аварий технических систем, с целью апробации разработанных ранее подходов и моделей. Расчеты выполнены для конструкций реальных объектов сложной структуры, находящихся в эксплуатации в течение длительного времени.
1. Показатели живучести технических систем.
Сформированы группы количественных показателей, отражающие различные аспекты живучести умеренно или сильно поврежденных деталей, элементов конструкций, или конструкций как структур или многоэлементных систем.
Для конструкций с развивающейся макроскопической трещиной (рис. 29) выполнено расчетно-экспериментальное исследование фактических коэффициентов запаса как интегрального показателя живучести.
Характерными являются результаты, полученные для конструктивной зоны образца I, содержащей трещину 1-1 (рис. 30).
Установлено, что количественные значения расчетных коэффициентов запаса по коэффициенту интенсивности напряжений оказываются наименьшими, приближаются к средним по конструкции коэффициентам запаса по напряжениям и характеризуются наименьшим рассеянием. Наибольшими оказываются расчетные коэффициенты запаса по скорости роста трещины и их рассеяние. Величины расчетных коэффициентов запаса по длине трещины и долговечности занимают промежуточное значение между всеми расчетными коэффициентами.
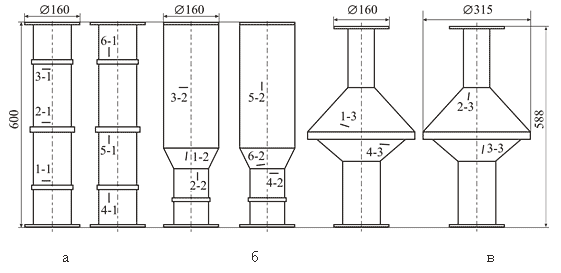
Рис. 29. Экспериментальные образцы с трещинами: а — образец I; б — образец II; в — образец III
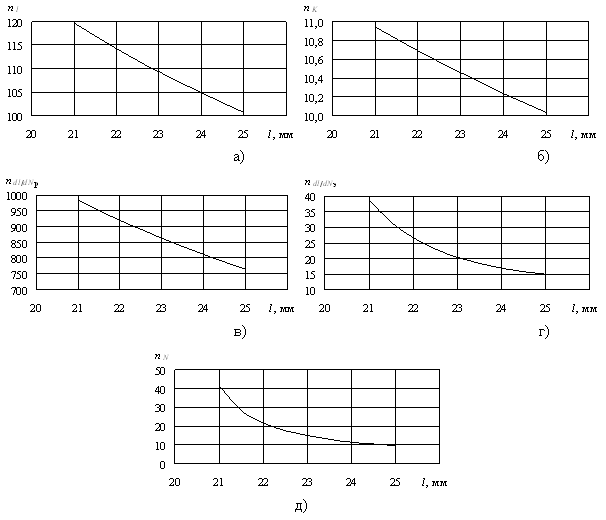
Рис. 30. Зависимость от длины развивающейся трещины коэффициента запаса по длине трещины (а), коэффициенту интенсивности напряжений (б), расчетной (в) и экспериментальной (г) скорости роста трещины, долговечности (д)
Таким образом, исследована динамика системы коэффициентов запаса с учетом кинетики роста трещин, которая может быть рассмотрена в качестве количественной характеристики живучести элементов конструкций с учетом возможного развития трещиноподобных дефектов.
2. Анализ живучести и аварийной ситуации металлоконструкции эстакады — подкрановой балки мостового крана грузоподъемностью 200 т.
Выполнено моделирование живучести и аварийной ситуации (АС) при воздействии нештатных нагрузок на металлоконструкцию эстакады, которая является подкрановой балкой мостового крана грузоподъемностью 200 т. Особенности задачи заключаются в уникальности погрузочно-разгрузочных работ (крупногабаритные трансформаторы для Богучанской ГЭС весом 220 т), длительном сроке эксплуатации конструкции (более 20 лет) и связанные с этим деградационные процессы (коррозионные и усталостные повреждения). Учитывая ограниченное число операций подъем-опускание груза и его перемещение, моделирование аварийной ситуации проводилось для предельного состояния, характеризующего нарушение несущей способности конструкции в результате приложения однократной максимальной статической нагрузки, без учета и с учетом коррозионных повреждений. Моделирование проводили на основе методики, разработанной в ходе выполнения проекта и включающей следующие этапы.
1. Анализ конструкции для определения структурных элементов и их соединений. Классификация элементов по степени опасности с точки зрения возможности разрушения.
2. Разработка сценария возникновения аварийных ситуаций для определенных видов предельных состояний и выявление возможных механизмов ее развития.
3. Поэтапное моделирование напряженно-деформированного состояния (НДС) конструкции в условиях предполагаемой аварийной ситуации. В качестве инициации аварийной ситуации рассматриваются разрушения наиболее нагруженных и наиболее опасных элементов. В дальнейших расчетах из модели последовательно исключаются элементы, в которых достигнуто предельное состояние. Вычисления повторяются до момента потери несущей способности конструкции в целом — превышение уровня максимальных эквивалентных напряжений допустимого значения — 186 МПа.
Анализ НДС конструкции эстакады в пределах консольно-подвесной части выполнен методом конечных элементов (МКЭ) с помощью программного комплекса ANSYS. Конечно-элементная модель включает более 1 млн. степеней свободы.
Учитывая расчетные значения параметров НДС конструкции, информацию о сроке и условиях эксплуатации, результаты диагностирования технического состояния эстакады, а также данные анализа типичных повреждений подобных конструкций, первым этапом в сценарии аварийной ситуации принято усталостное разрушение диафрагмы. Результаты моделирования аварийной ситуации для этого случая представлены на рис. 31 (для ясности часть поверхностей удалена), где указаны максимальные значения напряжений и зоны их действия на каждом этапе. Характерной особенностью развития АС является снижение на 4-м шаге уровня максимальных напряжений в конструкции до значений меньших, чем в исходном состоянии. Это обусловлено перераспределением напряжений за счет изменения жесткости отдельных частей балки, т.е. специфичным резервированием прочности. В результате наиболее нагруженной областью становится соединение вертикальной стенки с верхним поясом в месте крепления подкрановой балки к опоре А. Дальнейшие отказы элементов данного узла приводят к потере несущей способности конструкции в целом.
Другие расчетные варианты аварийной ситуации были основаны на сценариях, в которых первым шагом были приняты отказы в результате развития усталостных трещин наиболее нагруженных сварных соединений узлов крепления подкрановой балки к консольно-подвесной части эстакады. В зависимости от принятых начальных условий аварийные ситуации отличаются траекториями развития и количеством этапов. Также возможны случаи пересечения и совпадения отдельных участков траекторий. Результаты анализа позволили определить наиболее вероятные варианты развития аварийной ситуации и оценить устойчивость конструкции к катастрофическому разрушению, что явилось основой для назначения мероприятий, ведущих к повышению ее живучести.
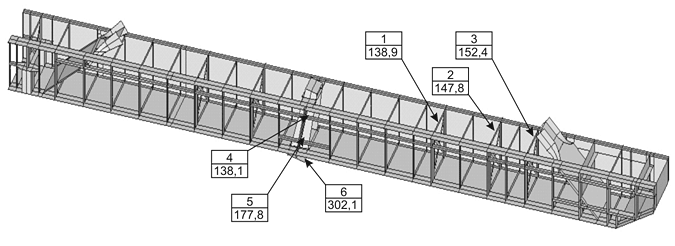
Рис. 31
3. Модельные расчеты долговечности разъемного соединения ГА2 Саяно-Шушенской ГЭС (СШГЭС).
По заданию рабочей группы ОЭММПУ РАН на основе посещения СШГЭС проведены предварительные расчетные оценки причин, источников и сценариев катастрофы 17 августа 2009 г.
Разработана модель живучести многокомпонентных систем (несущие разъемные соединения конструкций силовых агрегатов атомных реакторов, гидроагрегатов, газовых турбин), учитывающая накопление повреждений при нестационарных режимах нагружения и перераспределение аварийных нагрузок при наличии полностью или частично отказавших элементов.
На базе анализа НДС (рис. 32) и имеющейся информации о нагрузках и воздействиях выполнены модельные расчеты долговечности соединения крышки со статором гидротурбины.

Рис. 32
Расчеты осуществлялись на основе гипотезы линейного суммирования повреждений. Были определены режимы нагружения, вносящие основной вклад в уровень повреждений — циклы «пуск-остановка» гидроагрегата и регулирования мощности на переходных режимах. Получены значения ресурса данного соединения для различных режимов нагружения и оценка общего накопленного повреждения.
Основные публикации:
- Анискович Е. В., Лепихин А. М., Москвичев В. В.
Оценка опасности трещиноподобных дефектов в тонкостенных сосудах давления // Тяжелое машиностроение. — 2009. — № 1. — С. 22-24. - Буров А. Е.
Моделирование поведения металлоконструкции крановой эстакады при возникновении аварийной ситуации // Тр. III Всерос. конф. «Безопасность и живучесть технических систем». — Красноярск: ИВМ СО РАН. — 2009. — С. 123–126 . - Доронин С. В.
Оценка живучести оболочечных элементов конструкций с трещинопо-добными дефектами // Материалы IV Междунар. конф. «Проблемы механики современных машин». — Улан-Удэ: ВСГТУ. — 2009. — Т. 1. — С. 135–138 . - Доронин С. В.
Расчеты конструкций с дефектами и повреждениями в рамках концепции живучести технических систем // Тр. III Всерос. конф. «Безопасность и живучесть технических систем». — Красноярск: ИВМ СО РАН. — 2009. — Т. 3. — С. 38-39. - Лепихин А. М.
Задачи обеспечения безопасности больших технических систем // Тр. III Всерос. конф. «Безопасность и живучесть технических систем». — Красноярск: ИВМ СО РАН. — 2009. — С. 15-16. - Лепихин А. М.
Риск-анализ многокомпонентных систем с многоочаговыми повреждениями // Тяжелое машиностроение. — 2009. — № 6. — С. 23-25. - Лепихин А. М., Чернякова Н. А., Москвичев Е. В.
Особенности расчета ресурса трубопроводов на стадии роста усталостных трещин // Тр. I научн-практ. конф. «Экспертиза промышленной безопасности опасных производственных объектов в условиях Крайнего Севера: проблемы и пути решения». — Якутск. — 2009. — С. 16-18. - Москвичев В. В.
Особенности решения задач живучести и безопасности технических систем // Тр. III Всерос. конф. «Безопасность и живучесть технических систем». — Красноярск: ИВМ СО РАН. — 2009. — С. 12-14. - Сигова Е. М., Доронин С. В.
Выбор коэффициентов запаса прочности с учетом кинетики трещиноподобных дефектов // Материалы IV Междунар. конф. «Проблемы механики современных машин». — Улан-Удэ: ВСГТУ. — 2009. — Т. 2. — С. 228–231 . - Сигова Е. М., Доронин С. В.
Расчетно-экспериментальная оценка коэффициентов запаса в конструкциях с развивающейся усталостной трещиной // Вестник СибГАУ. — 2008. — Вып. 4 (21). — С. 94-99. - Черняев А. П.
Экспертиза технического состояния и оценка безопасного ресурса оборудования технических систем // Тр. III Всерос. конф. «Безопасность и живучесть технических систем». — Красноярск: ИВМ СО РАН. — 2009. — С. 88. - Чернякова Н. А.
Оценка ресурса элементов конструкций на стадии роста усталостных трещин // Материалы IV Междунар. конф. «Проблемы механики современных машин». — Улан-Удэ: ВСГТУ. — 2009. — Т. 3. — С. 243–244 . - Чернякова Н. А.
Статистические оценки ресурса элементов конструкций на стадии роста усталостных трещин // Тр. III Всерос. конф. «Безопасность и живучесть технических систем». — Красноярск: ИВМ СО РАН. — 2009. — С. 271.
(Отдел машиноведения)
| К началу | |