| ИВМ СО РАН | Поиск |
| Отчеты ИВМ СО РАН |
Отчет ИВМ СО РАН за 2007 год
Программы РАН
Отделение математических наук
Программа № 1.3 «Современные вычислительные и информационные технологии решения больших задач»
Проект № 1.3.3 «Разработка и исследование вычислительных алгоритмов решения уравнений вязкой несжимаемой жидкости и их применение к задачам гидрофизики»Руководитель: чл.-корр. РАН В. В. Шайдуров
Моделирование поверхностных волн в акваториях в пределах приемлемой точности описывается в рамках теории мелкой воды. Задача рассмотрена с учетом сферичности Земли и сил Кориолиса. Число Россби (отношение силы инерции к силе Кориолиса) считается малым, что позволило пренебречь нелинейными слагаемыми за исключением членов, учитывающих донное трение.
Рассмотренная модель допускает решение как прямой задачи для уравнений мелкой воды (т.е. по известным краевым и начальным данным восстанавливать вектор скорости и возвышение свободной поверхности во всей акватории), так и решать задачу о восстановлении решения по наблюдениям за возвышением свободной поверхности на границе области. В последнем случае методом последовательных приближений восстанавливается неизвестная функция в граничных условиях, так, чтобы прямое решение задачи на границе, где заданы наблюдаемые значения свободной поверхности, в некотором смысле было близко к известному. Для этого на каждом временном слое необходим итерационный процесс последовательного решения прямой и обратной задач для дискретизированной по времени исходной системы с уточнением на каждой итерации граничных условий.
Для модели проведены дискретизации по времени и пространству на основе метода конечных элементов с билинейными на каждом треугольнике базисными функциями и последующим применением квадратурных формул.
Создано, отлажено и протестировано программное обеспечение, реализующее решение как прямой задачи, так и задачи с усвоением данных наблюдений.
Для исследования скорости сходимости итерационного процесса восстановления граничной функции по данным наблюдений было проведено три численных эксперимента.
В первом эксперименте параметр регуляризации α полагался равным нулю, задавались «наблюдения» на жидкой части границы, т.е точно определялось возвышение свободной поверхности ξobs. Затем проводилось восстановление граничной функции d. Восстановленная функция d принималась за «точную» граничную функцию, и далее, используя данные наблюдений ξobs, проводилось повторное восстановление d с вычислением относительной и абсолютной погрешностей восстанавливаемых функций dnum и ξnum на границе (рис. 37).
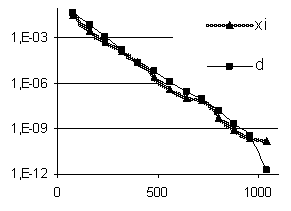
Рис. 37. Зависимость относительных погрешностей от числа итераций
Во втором и третьем экспериментах считалась известной граничная функция d, для которой путем решением прямой задачи определялось «точное» решение ξ, значения которого на границе принимались за наблюдаемые ξobs. Далее используя данные наблюдений проводилось повторное восстановление d с вычислением относительной погрешности восстанавливаемых функций, а также равномерных норм абсолютной погрешности. Во втором эксперименте параметр регуляризации полагался равным нулю, в третьем эксперименте параметр регуляризации отличался от нуля.
Экстраполяция Ричардсона позволяет повысить точность численного решения, проводя вычисления для нескольких последовательных не очень малых значений параметра регуляризации, а затем комбинируя полученные решения. Сходимость численного метода при малых значениях параметра регуляризации ухудшается, если наблюдения ξobs заданы на части жидкой границы. Кроме того, замедляет сходимость при малых значениях α наличие случайных ошибок, вносимых при измерении ξobs. Поэтому использование экстрополяции Ричардсона для повышения точности расчетов оправдана.
Для численных экспериментов по экстраполяции использовалась сетка, построенная только для той части Мирового океана, где глубины не менее 200~м. Сетка состоит из 4709 узлов и 8358 треугольных элементов. В качестве точного решения и для задания соответствующих данных наблюдений рассматривалось численное решение прямой задачи при заданной граничной функции d. Далее для разных значений параметра регуляризации α проводилось восстановление функции d. В качестве начального приближения бралась d = 0 на всей границе. На рис. 38 приведен вид заданной и восстановленной функций d на границах Мирового океана при α = 5e − 5.
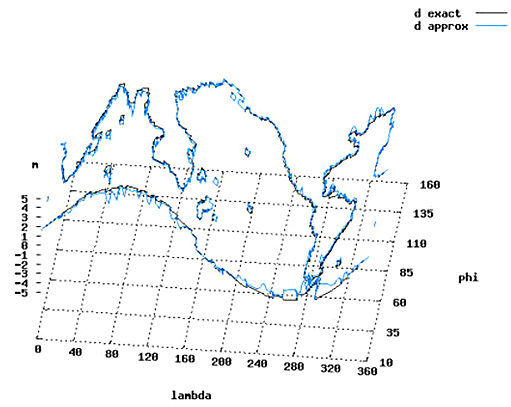
Рис. 38. Заданная и восстановленная функция d
Для различных значений параметра α проводилось фиксированное количество итераций уточнения d. Экстраполяция Ричардсона проводилась по двум и трем решениям для последовательных значений параметра оптимизации α. Экстраполяция показала свою эффективность, но требуется продолжение исследований.
Подготовлена также версия программы для расчетов на массивно-параллельных компьютерах с общей памятью.
Основные публикации:
- Agoshkov V. I., Kamenshchikov L. P., Karepova E. D., Shaidurov V. V.
Numerical solution of some direct and inverse mathematical problems for tidal flows // Notes on Numerical Fluid Mechanics and Multidisciplinary Design. — Springer (принята к печати). - Каменщиков Л. П., Карепова Е. Д., Шайдуров В. В.
Моделирование распространения крупномасштабных волн в морях и океанах с параллельной реализацией // Тр. IV Сибирской школы-семинара по параллельным и высокопроизводительным вычислениям (принята к печати).
(Отдел вычислительной математики)
| К началу | |