| ИВМ СО РАН | Поиск |
| Отчеты ИВМ СО РАН |
Отчет ИВМ СО РАН за 2005 год
Важнейшие научные достижения 2005 года
- Важнейшие научные достижения 2005 года
- Вычислительный алгоритм для определения динамики взвешенных идонных наносов в речном русле
- Математическая модель магнитного барьера, возникающего при обтекании солнечным ветром магнитных и немагнитных планет
- Расчетно-экспериментальные методы оценки живучести конструкций в аварийных ситуациях
- Расчеты ударных волн уплотнения в сыпучей среде
- Алгоритмы быстрого построения главных многообразий в задачах обработки данных
Вычислительный алгоритм для определения динамики взвешенных идонных наносов в речном русле
Номер научного направления ОИТВС: 2
Авторы научного результата:
Белолипецкий В. М., зав. отделом, д.ф.-м.н., проф.;
Генова С. Н., н.с., к.т.н.
Тел.:
Построены математические модели динамики взвешенных и донных наносов в речном русле. Математическая модель динамики донных наносов в руслах рек и каналов основана на приближении вязкопластической среды Бингама. Используются упрощенные уравнения медленных движений тонкого слоя вязкопластической среды для осредненных по поперечному сечению реки параметров.
Совместно с Институтом биофизики СО РАН разработан первый уровень вычислительных моделей для исследования переноса примесей и миграции радионуклидов по компонентам речной экосистемы. Выполнена настройка вычислительного алгоритма на реальные участки р. Енисей, определены зоны заиления и транзита наносов.
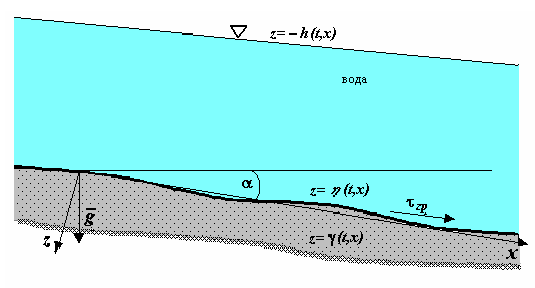
Рис. 1. Схема продольного сечения русла реки.
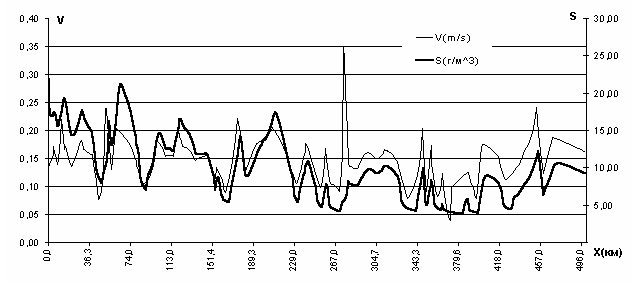
Рис. 2. Скорость течения и мутность воды на участке от г. Красноярска до г. Енисейска.
Важнейшие публикации:
- Дегерменджи А. Г., Косолапова Л. Г., Белолипецкий В. М.
Прогнозная радиоэкологическая математическая модель реки Енисей // Радиационная биология. Радиоэкология. — 2002. — Т. 42. — № 4. — C. 459–465 . - Белолипецкий В. М., Генова С. Н.
Вычислительный алгоритм для определения динамики взвешенных и в донных наносов в речном русле // Вычислительные технологии. — 2004. — T. 9. — № 2. — С. 9-25. - Закономерности распределения и миграции радионуклидов в долине реки Енисей / Сухоруков Ф. В., Дегерменджи А. Г., Белолипецкий В. М. и др.
— Новосибирск: Изд-во СО РАН, филиал «Гео», 2004. — 286 с.
| К началу | |
Математическая модель магнитного барьера, возникающего при обтекании солнечным ветром магнитных и немагнитных планет
Номер научного направления ОИТВС: 2
Авторы научного результата:
Еркаев Н. В., в.н.с., д.ф.-м.н., проф;
Мезенцев А. В., гл.специалист, к.ф.-м.н.;
Шайдуров В. А., н.с., к.ф.-м.н.
Тел.:
Впервые разработана общая математическая модель магнитного барьера, возникающего при обтекании солнечным ветром различных планет, как магнитных (типа Земли), так и немагнитных (типа Венеры), и обеспечивающего сильное влияние межпланетного магнитного поля на характер взаимодействия солнечного ветра с обтекаемыми космическими телами. Межпланетное магнитное поле имеет относительно малую интенсивность в солнечном ветре, но значительно возрастает в областях магнитного барьера, представляющих собой тонкие пограничные слои вблизи обтекаемых поверхностей. Определены аналитические асимптотики для параметров магнитного барьера при больших числах Маха-Альвена. На основе аппроксимаций пограничного слоя получены уравнения магнитного барьера, решения которых найдены конечно-разностным методом. В результате получены новые зависимости, характеризующие распределения магнитного поля и параметров плазмы между головной ударной волной и обтекаемой границей для различных направлений межпланетного магнитного поля и чисел Маха-Альвена. В случае магнитных планет, при определённой ориентации межпланетного магнитного поля, магнитный барьер является фоном для развития процесса быстрого пересоединения магнитных полей на обтекаемой границе магнитосферы. Получены новые нестационарные решения, описывающие фазы формирования и усиления магнитного барьера после его внезапного ослабления, вызванного импульсом магнитного пересоединения. Для немагнитных планет важную роль играют процессы нагружения солнечного ветра холодными ионами, образующимися в области магнитного барьера за счёт ионизации атмосферных атомов и формирующими слой холодной плотной плазмы вблизи обтекаемой границы ионосферы. Исследовано влияние интенсивности загрузки на профили магнитного поля и параметров плазмы между границей ионосферы и головной ударной волной. Показано, что магнитный барьер способствует развитию неустойчивости Кельвина-Гельмгольца на обтекаемой границе, вызывая обмен импульсом между солнечным ветром и плазмой внутри магнитосферы (для магнитных планет) или ионосферы (для немагнитных планет).
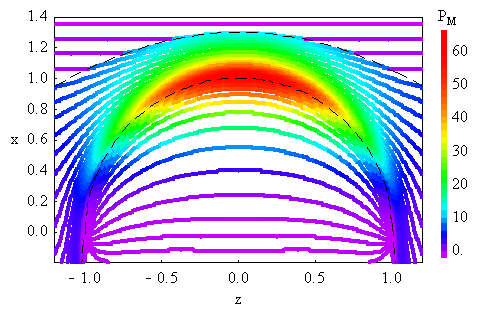
Рис. 3. Распределение магнитного давления в области обтекания солнечным ветром ионосферы Венеры.
На рис. 3 показан вариант модельного расчёта распределения магнитного давления вдоль магнитных силовых линий в области обтекания солнечным ветром ионосферы Венеры (проекция на плоскость XZ). Магнитное давление нормировано к динамическому давлению солнечного ветра s Vs2, где s, Vs — массовая плотность и скорость набегающего потока. Координаты XZ нормированы к радиусу обтекаемой поверхности. В данной модели набегающий поток направлен навстречу оси X, а межпланетное магнитное поле — вдоль оси Z. Штриховые линии обозначают положение отошедшей ударной волны и обтекаемой границы в плоскости XZ. Область повышенного магнитного давления, выделенная красным цветом, представляет собой магнитный барьер, располагающийся вблизи границы ионосферы.
Важнейшие публикации:
- Erkaev N. V., Farrugia C. J., Biernat H. K., Mezentsev A. V., Shaidurov V. A. Magnetohydrodynamic aspects of solar wind interaction with the magnetosphere // Solar Planetary Relations, Eds. Biernat H. K., Lammer H., Vogl D. F., Muehlbachler S.
, Research Signpost. — 2005. — P.89–112 . - Erkaev N. V., Farrugia C. J., Biernat H. K.
Variations of magnetic field and plasma parameters in the magnetosheath related to reconnection pulses // Adv. Space Res. — 2004. — Vol. 33. — P. 784–788 . - Erkaev N. V., Farrugia C. J., Biernat H. K.
The role of the magnetic barrier in the Solar wind-magnetosphere interaction // Planetary and Space Sciences. — 2003. — Vol. 51. — № 12. — P. 745–755 . - Erkaev N. V., Biernat H. K., Vogl D. F., Farrugia C. J.
MHD modelling of the magnetosheath with anisotropic plasma pressure // Adv. Space Res. — 2001. — Vol. 28. — P. 873–877 . - Erkaev N. V., Farrugia C. J., Biernat H. K.
MHD effects in the Venus magnetosheath including mass loading // Adv. Space Res. — 2001. — Vol. 28. — P. 833–839 . - Erkaev N. V., Farrugia C. J., Biernat H. K.
Ideal magnetohydrodynamic flow around a blunt body under anisotropic pressure // Physics of Plasmas. — 2000. — Vol. 7. — P. 3413–342 0. - Erkaev N. V., Biernat H. K., Farrugia C. J., Quinn J. M.
Magnetosheath flow model with anisotropic pressure // Adv. Space Res. — 2000. — Vol.25. — № 7/8. — P. 1523–152 8.
| К началу | |
Расчетно-экспериментальные методы оценки живучести конструкций в аварийных ситуациях
Номер научного направления ОИТВС: 2
Авторы научного результата:
Москвичев В. В., зав. отделом, д.т.н., проф.;
Лепихин А. М., в.н.с, д.т.н.;
Доронин С. В., с.н.с., к.т.н., доцент;
Буров А. Е., н.с., к.т.н.;
Черняев А. П., с.н.с., к.т.н.;
Чернякова Н. А., м.н.с.
Тел.:
В развитие расчетно-экспериментальных методов анализа конструкционной прочности, долговечности, трещиностойкости и надежности несущих конструкций технических систем сформулирована методология оценки их живучести при наличии недопустимых по нормам проектирования дефектов и повреждений (переход от штатных условий эксплуатации в предельное и аварийное состояния).
Система показателей живучести включает характеристики номинального и локального напряженных состояний, механических свойств и трещиностойкости, параметры уравнений предельных состояний и кинетических соотношений, показатели вероятностей безотказной работы и ресурса рассчитываемых для потенциально опасных зон конструкций в детерминированной и вероятностной постановках.
Случайный характер номинальной нагруженности учитывается вероятностным описанием локальных полей напряжений и деформаций в вершинах трещин. Статистическая обработка параметров механики разрушения, описывающих напряженно-деформируемое состояние (НДС) в вершине трещины, показала, что коэффициенты интенсивности напряжений и значения J-интеграла распределены по нормальному или двухпараметрическому закону Вейбулла.
Выполненные расчеты НДС позволили сформулировать критерии чувствительности конструктивных элементов к наличию трещины на различных стадиях развития аварийной ситуации до полной потери несущей способности конструкции.
Для совместного рассмотрения характеристик НДС, параметров технологической и эксплуатационной дефектности предложены параметрические модели технологической и эксплуатационной дефектности, связывающие вероятностные параметры дефекта с уровнем интенсивности напряжений в области дефекта.
Конечные результаты представляются в виде полных вероятностных диаграмм и поверхностей живучести, связывающих уровень номинальной нагруженности, вероятности безотказной работы и показатели ресурса в зависимости от эксплуатационных факторов.
Важнейшие публикации:
- Лепихин А. М., Махутов Н. А., Москвичев В. В., Черняев А. П.
Вероятностный риск-анализ конструкций технических систем. — Новосибирск: Наука. — 2003. — 174 с. - Доронин С. В., Лепихин А. М., Москвичев В. В., Шокин Ю. И.
Моделирование прочности и разрушения несущих конструкций технических систем. — Новосибирск: Наука, 2005. — 250 с. - Доронин С. В.
Формализация сценариев развития и оценка риска аварийных ситуаций несущих конструкций // Безопасность труда в промышленности. — 2005. — № 3. — С. 54-57. - Москвичев В. В., Лепихин А. М., Черняев А. П. Остаточный ресурс и риск-анализ конструкций технических систем // Fracture Mechanics of Materials and Structural Integrity / Editor V. V. Panasyuk
. — Lviv: Karpenko Physico-mechanikal institute. — 2004. — P. 433–438 . - Шокин Ю. И., Буров А. Е., Доронин С. В., Крушенко Г. Г., Лепихин А. М., Москвичев В. В., Черняев А. П.
Модельные расчеты прочности и разрушения конструкций технических систем // Вычислительные технологии. — 2004. — Т. 9. — С. 101–111 . - Moskvichev V. V.
Safety problems of technical objects // Notes on numerical fluid mechanics and multidisciplinary design. Computational Science and High Performance Computing. — Springer. — 2005. — Vol. 88. — P. 112–122 .
| К началу | |
Расчеты ударных волн уплотнения в сыпучей среде
Номер научного направления ОИТВС: 2
Авторы научного результата:
Садовский В. М., зав. отделом, д.ф.-м.н., проф.;
Садовская О. В., н.с, к.ф.-м.н.
Тел.:
Разработан комплекс параллельных программ для численного решения задач динамики упругопластических и сыпучих сред в пространственной постановке, который позволяет анализировать процессы распространения волн напряжений и деформаций в массиве, составленном из произвольного числа разнородных блоков с криволинейными поверхностями раздела. На его основе проведена серия расчетов взаимодействия ударных волн уплотнения (сигнотонов), генерируемых периодической импульсной нагрузкой на границе массива неоднородно разрыхленной сыпучей среды, с образованием поперечного кумулятивного выплеска.
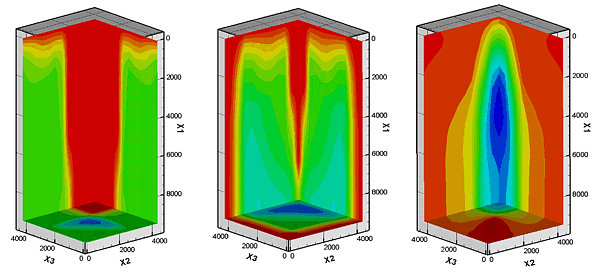
Рис. 4. Поле напряжений в задаче кумулятивного взаимодействия сигнотонов: в результате отражения искривленных волновых фронтов на центральной оси появляется кумулятивный выплеск (характерная зона сжимающих напряжений, движущаяся снизу вверх). Расчеты проведены на многопроцессорной вычислительной системе МВС-15000 Межведомственного суперкомпьютерного центра (г. Москва).
Важнейшие публикации:
- Садовский В. М.
К теории распространения упругопластических волн в сыпучих средах // Докл. РАН. — 2002. — Т. 386. — № 4. — С. 487–489 . - Садовская О. В., Садовский В. М.
К исследованию упругопластических волн в сыпучей среде // ПМТФ. — 2003. — Т. 44. — № 5. — С. 168–176 . - Садовская О. В.
Метод сквозного счета для исследования упругопластических волн в сыпучей среде // Журнал вычислительной математики и математической физики. — 2004. — Т. 44. — № 10. — С. 1909–192 0. - Садовская О. В., Садовский В. М.
Параллельная реализация алгоритма для расчета упругопластических волн в сыпучей среде // Вычислительные методы и программирование. — 2005. — Т. 6. — С. 209–216 . - Sadovskii V. M., Sadovskaya O. V.
Parallel computation of elastic-plastic waves propagation in granular material // Proc. 7-th Int. Conf. on Mathematical and Numerical Aspects of Wave Propagation «Waves 2005». — USA, Brown University. — 2005. — P. 223–225 .
| К началу | |
Алгоритмы быстрого построения главных многообразий в задачах обработки данных
Номер научного направления ОИТВС: 3
Авторы научного результата:
Горбань А. Н., зав. отделом, д.ф.-м.н., проф.;
Зиновьев А. Ю., н.с., к.ф.-м.н.;
Тел.:
Завершен цикл работ по построению главных многообразий в задачах обработки данных. Главные многообразия определяются как линии или поверхности, проходящие «через середину» распределения данных. Построены, реализованы и апробированы алгоритмы быстрого построения главных многообразий априорно заданной топологии. Они основаны на механических аналогиях главных многообразий с упругими мембранами и пластинами. На каждом шаге метод приводит к задаче минимизации квадратичного функционала с разреженной матрицей. Предложены и реализованы адаптивные стратегии оптимизации. Обособленные «главные объекты», не являющиеся многообразиями (графы, кубические комплексы), также строятся предложенными методами. Алгоритмы и программное обеспечение апробированы на множестве задач реальной сложности и широко используются в различных институтах России и Европы.
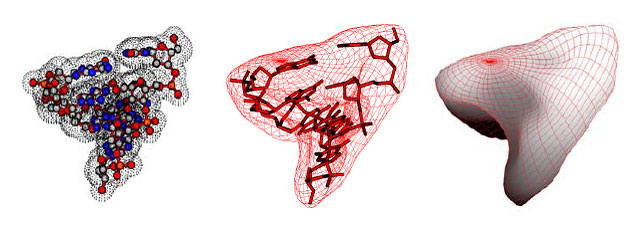
Рис. 5. Главная поверхность сферической топологии для аппроксимации молекулярной поверхности Ван дер Ваальса для биологической молекулы.
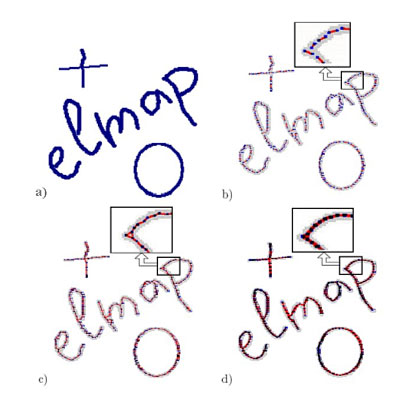
Рис. 6. Скелетонизация образов с использованием главных кривых: a) исходный образ; b) вычисление локальных главных компонент; c) построение связного графа; d) оптимизация положения вершин графа.
Важнейшие публикации:
- Gorban A., Zinovyev A.
Elastic Principal Graphs and Manifolds and their Practical Applications // Computing. — 2005. — Vol. 75. — № 4. — P. 359–379 .
| К началу | |