| ИВМ СО РАН | Поиск |
| Отчеты ИВМ СО РАН |
Отчет ИВМ СО РАН за 2011 год
Проекты СО РАН
- Междисциплинарные интеграционные проекты
- Проект № 4. «Информационные технологии, математические модели и методы мониторинга и управления экосистемами в условиях стационарного, мобильного и дистанционного наблюдения»
- Проект № 26. «Математические модели, численные методы и параллельные алгоритмы для решения больших задач СО РАН и их реализация на многопроцессорных суперЭВМ»
- Проект № 40. «Термодинамические согласованные модели сплошных сред и их вычислительное моделирование: вычислительные модели, алгоритмы и их программная реализация; новые критерии устойчивости движения, позволяющие указывать допуски на определяющие параметры»
- Проект № 50. «Модели изменения биосферы на основе баланса углерода (по натурным и спутниковым данным и с учетом вклада бореальных экосистем)»
- Проект № 65. «Теоретико-групповые и геометрические методы исследования нелинейных моделей механики сплошных сред и математической физики: точные решения, интегрируемость, сигулярности»
- Проект № 95. «Комплексные исследования механизмов стратификации биологических, химических и физических компонент водных экосистем как основа для прогноза и управления качеством воды»
- Проект № 116. «Антропогенные риски угледобывающих и нефтегазодобывающих территорий Сибири»
- Проекты СО РАН, выполняемые совместно со сторонними научными организациями
- Заказной проект СО РАН
- Программа сибирского отделения РАН «Телекоммуникационные и мультимедийные ресурсы СО РАН»
- Программа сибирского отделения РАН «Высокопроизводительные вычисления СО РАН»
- Экспедиционные проекты СО РАН
- Лаврентьевский грант молодым ученым СО РАН
Междисциплинарные интеграционные проекты
Проект № 4. «Информационные технологии, математические модели и методы мониторинга и управления экосистемами в условиях стационарного, мобильного и дистанционного наблюдения»
Руководитель проекта: академик РАН Ю. И. Шокин
Ответственный исполнитель ИВМ СО РАН: к.ф.-м.н. О. Э. Якубайлик
Исполнители: к.т.н. А. А. Кадочников, к.т.н. А. В. Токарев, А. А. Гостева, М. Г. Ерунова, А. Г. Матвеев, А. С. Пятаев
Исследования ИВМ СО РАН по указанному интеграционному проекту связаны со следующими задачами:
- Публикация в Интернете оперативных данных по лесным пожарам (для ГУП Красноярского края «Лесопожарный центр»).
- Формирование программно-технологического обеспечения для интеграции и аналитической обработки формируемых информационных ресурсов мониторинга состояния окружающей природной среды в зоне действия предприятий нефтегазовой отрасли Красноярского края.
Результаты работ состоят в следующем:
- Разработана технология публикации оперативных данных по лесным пожарам Красноярского края на веб-карте. Выполнены проектирование и разработка информационного и программного обеспечения этой задачи, разработан программный модуль «Карта пожарной обстановки» в котором реализованы следующие функции: автоматический импорт данных о пожарах и их динамике из обменного XML-формата по расписанию; многокритериальная фильтрация пожаров по периоду времени, авиаотделениям, лесничествам, типам и статусам пожаров; визуализация выборки из пожаров на интерактивной карте Красноярского края; отображение динамики пожара, его статуса, площади, количества задействованных людей и использованных средств тушения. Созданный модуль размещен на официальном сайте ГУП Красноярского края «Лесопожарный центр» (Рис V.1).
- Проведены работы по модернизации, повышению эффективности работы программного обеспечения информационной системы мониторинга состояния окружающей природной среды в зоне действия предприятий нефтегазовой отрасли. Изменения связаны с корректировкой информационной модели системы, состава баз данных, реорганизацией структуры хранения геопространственных данных и интерфейсов доступа к ним. Новая подсистема управления метаданными значительно облегчает доступ к информации.
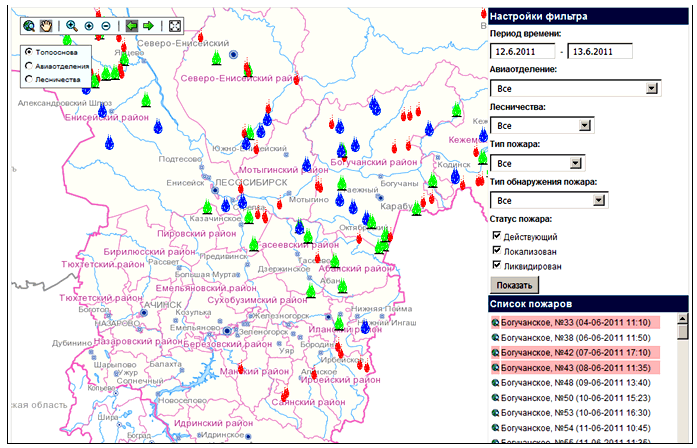
Рис. V.0. Оперативные данные по лесным пожарам Красноярского края на веб-карте
Основные публикации:
- Якубайлик О. Э., Гостева А. А., Ерунова М. Г., Кадочников А. А., Матвеев А. Г., Пятаев А. С., Токарев А. В.
Информационное обеспечение задач мониторинга состояния окружающей природной среды в зоне действия предприятий нефтегазовой отрасли // Сб. тр. XI Всерос. конф. с участием иностранных ученых «Проблемы мониторинга окружающей среды» (EM-2011). — Кемерово: КемГУ. — 2011. — 388 с., ISBN 978-5-8353–116 9-9. — С. 273–278 . - Якубайлик О. Э.
Методы построения прикладных геоинформационных систем на основе картографических веб-сервисов геопортала // Математические и информационные технологии, MIT-2011 [Электронный ресурс] / Международная конференция (IX конференция «Вычислительные и информационные технологии в науке, технике и образовании»), Врнячка Баня, Сербия, 27-31 августа 2011 г., Будва, Черногория, 31 августа — 5 сентября 2011 г., № гос. регистрации — 0321102644, Режим доступа: http://conf.nsc.ru/ files/conferences/MIT-2011/abstracts/50895/50896/YakubailikOE.doc, свободный. — Загл. с экрана (дата обращения: 15.11.2011). - Кадочников А. А.
Разработка картографических сервисов для информационно-аналитических систем в региональном управлении // Математические и информационные технологии, MIT-2011 [Электронный ресурс] / Междунар. конф. (IX конф. «Вычислительные и информационные технологии в науке, технике и образовании»), Врнячка Баня, Сербия, 27-31 августа 2011 г., Будва, Черногория, 31 августа — 5 сентября 2011 г., № гос. регистрации — 0321102644, Режим доступа: http://conf.nsc.ru/ files/ conferences/ MIT-2011/ fulltext/ 50479/56591/ KadochnikovAA.pdf, свободный. — Загл. с экрана (дата обращения: 15.11.2011). — 5 с.
(Отдел вычислительной физики)
| К началу | |
Проект № 26. «Математические модели, численные методы и параллельные алгоритмы для решения больших задач СО РАН и их реализация на многопроцессорных суперЭВМ»
Руководитель проекта: академик РАН Б. Г. Михайленко
Ответственный исполнитель от ИВМ СО РАН: к.ф.-м.н., доц. Е. Д. Карепова
Исполнители: В. В. Шайдуров, Е. В. Дементьева, А. В. Малышев
В отчетный период продолжены исследования, связанные с моделированием поверхностных волн в больших акваториях.
Прямая задача для уравнений мелкой воды ставится в области произвольной формы на сфере с достаточно гладкой границей. Граница области состоит из Г1 «твердых» участков — береговой линии и Г2 «жидких» участков — граница по морю. На Г0 части «жидкой» границы известны данные наблюдений за свободной поверхностью.
В общем случае граничные условия на «жидкой» границе содержат граничную функцию, которую следует найти вместе с неизвестными задачи — скоростями и возвышением свободной поверхности. В области поставлена задача о восстановлении граничной функции по данным наблюдений, для решения которой используются методы оптимизации и теории управления.
Рассмотрено два семейства задач оптимального управления, отличающихся видом штрафной функции в функционале стоимости:
\[J^{I} (d,\xi (d))=\frac{1}{2} g\left(\alpha \int _{\Gamma }m_{2} \sqrt{gH} d^{2} ds +\int _{\Gamma }m_{0} \sqrt{gH} \left(\xi -\xi _{obs} \right)^{2} ds \right), (V.1)\] \[J^{II} (d,\xi (d))=\frac{1}{2} g\left(\alpha \int _{\Gamma }m_{2} \sqrt{gH} \left(\frac{\partial d}{\partial s} \right)^{2} ds +\int _{\Gamma }m_{0} \sqrt{gH} \left(\xi -\xi _{obs} \right)^{2} ds \right). (V.2)\]
Построен итерационный численный метод восстановления граничной функции и, следовательно, решения обратной задачи в области. Метод состоит в итерационном уточнении граничной функции d путем численного решения последовательно прямой и сопряженной задач.
Численное решение прямой и сопряженных задач основано на методе конечных элементов, для чего реализовано параллельное ПО с использованием технологий MPI и OpenMP.
На рис. V.1 изображен общий вид расчетной сетки, соответствующей акватории Охотского моря с прилегающей частью Тихого океана. На рис. V.2 (а-г) показано решение прямой задачи, соответствующей распространению начального возмущения в случае, когда источник (например, цунами) находится внутри области, а на рис. V.3 (а-г) — распространение возмущения приходящего с океана (источник находится за пределами расчетной области).
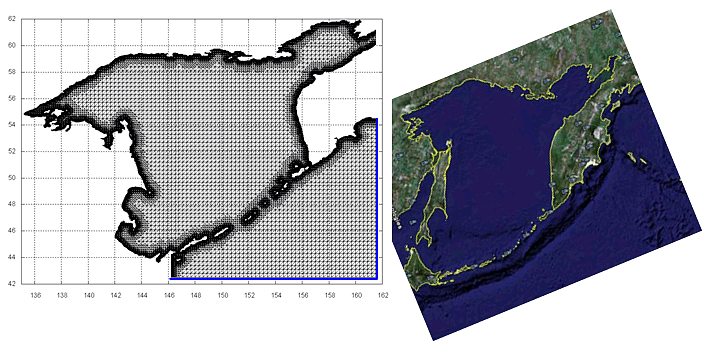
Рис. V.1. Общий вид сетки (слева) для акватории Охотского моря (справа)
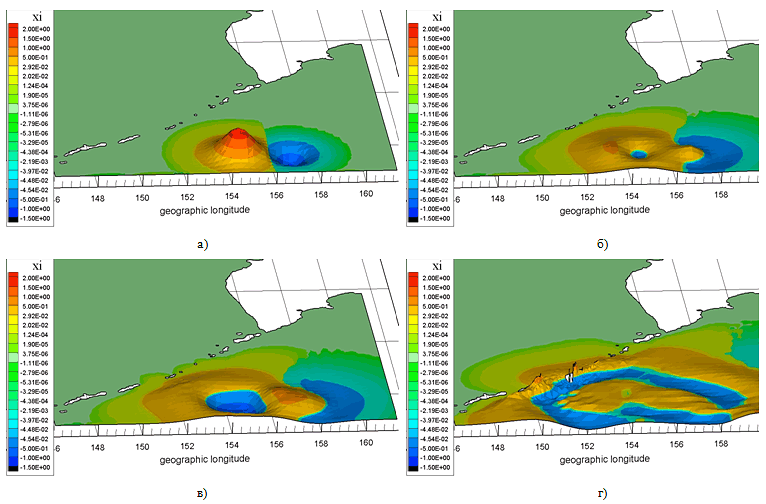
Рис. V.2. Распространение начального возмущения от источника, расположенного внутри расчетной области (акватория Охотского моря)
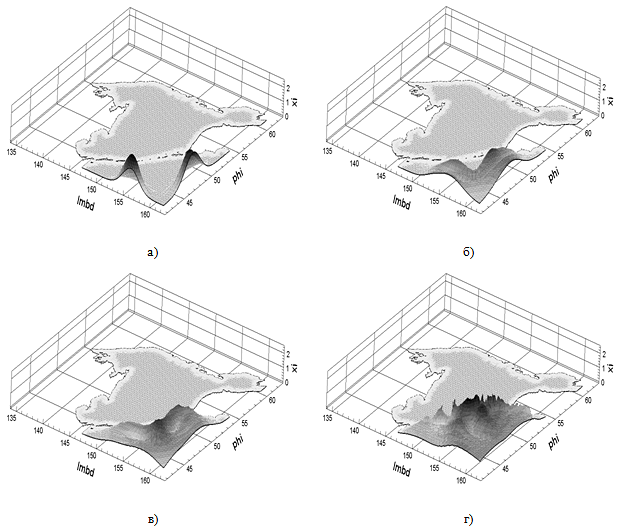
Рис. V.3. Распространение возмущения, приходящего от источника, расположенного вне расчетной области (акватория Охотского моря)
Установившееся решение принималось в качестве начальных данных, а за данные наблюдений на границе принимались отметки свободной поверхности $\textit{$\xi $}$ из установившегося решения, а значения функции $\textit{d}$ «забывались». Далее целью численных экспериментов являлось восстановление функции $\textit{d}$ по всей границе по морю (решение обратной задачи). Для этого, начиная с $\textit{d $\equiv$ 0}$, всюду на границе по морю восстанавливалась $\textit{d}$ по предлагаемому итерационному алгоритму.
Используемая процедура установления дает в качестве данных наблюдений функцию хорошей гладкости. Однако реальные данные наблюдений такой гладкостью, как правило, не обладают. В связи с этим в некоторых численных экспериментах на полученные после установления значения $\textit{$\xi $ }$на границе $\textit{Г${}_{0}$}$ был наложен белый шум. Затем зашумленные значения $\textit{$\xi $}$ брались в качестве наблюдаемых данных (рис. V.4, a). Более того, в части экспериментов рассматривались данные наблюдений с пропусками, т.е. заданные только на части границы по морю (рис. V.4, b).
Таким образом, обратная задача решалась с использованием функционалов стоимости (V.1) — (V.2) в двух различных постановках относительно задания данных наблюдений.
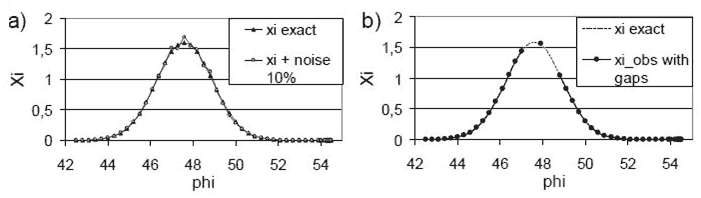
Рис. V.4. Данные, принимаемые за наблюденые на одной из границ по морю: a) гладкие и зашумленные 10%-ым белым шумом, b) заданные на части границы
1. Восстановление с зашумленными данными наблюдений (рис. V.4, a). При использовании функционала стоимости (V.1) восстановление произошло за 19 итераций к зашумленным данным (рис. V.5). В этом случае функция $\textit{d}$ оказалась очень чувствительной к внесенным погрешностям в данные наблюдений вплоть до потери гладкости, при этом отклонение от точного решения граничной функции $\textit{d}$ в некоторых точках достигает 23%. Отметим, что при этом ошибка в равномерной норме восстановленного уровня свободной поверхности $\textit{$\xi $}$ имеет порядок 10${}^{-5}$.
При использовании функционала стоимости (V.2) восстановление произошло за 40 итераций, причем восстановленная функция d сохраняет гладкость точной, несмотря на внесенные погрешности в данные наблюдений (рис. V.6). В отличие от предыдущего случая восстановленные на границе отметки уровеня $\textit{$\xi $ }$практически совпадают с незашумленными данными наблюдений, т.е. при восстановлении происходит сглаживание погрешностей, внесенных шумом.
2. Восстановление с гладкими данными наблюдений, заданными на части границы по морю (рис. V.4, b). При использовании функционала стоимости (V.1) функция $\textit{d}$ восстановилась лишь в точках, где наблюдения были заданы. В точках, в которых данные наблюдений о возвышении свободной поверхности отсутствовали, значения функции $\textit{d }$на протяжении всего процесса восстановления оставались практически неизменными, равными первоначально заданному $\textit{d=0}$.
При использовании функционала стоимости (V.1) (рис. V.7) предлагаемый метод восстанавливает отметки уровеня $\textit{$\xi $}$ и функцию $\textit{d}$ по всей жидкой границе, включая точки, в которых данные наблюдений не были заданы. Восстановление проходит за 142 итерации и демонстрирует хорошее согласование восстановленных значений с точным решением.
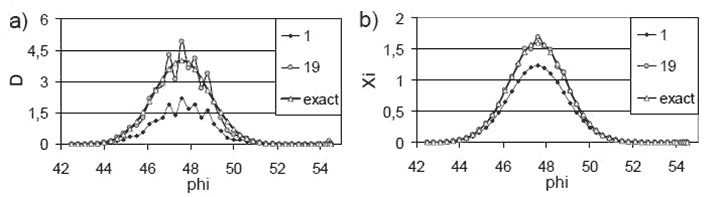
Рис. V.5. Итерационное восстановление функций $\textit{d}$(а) и $\textit{$\xi $}$(b) на одной из жидких границ для зашумленных данных наблюдений. Функционал стоимости (V.1)
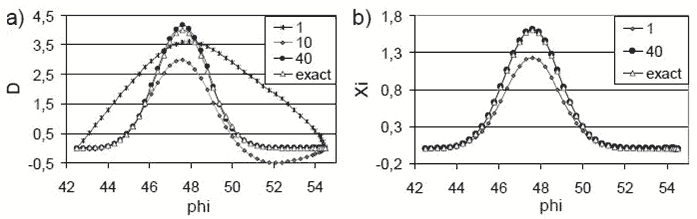
Рис. V.6. Итерационное восстановление функций $\textit{d}$(а) и $\textit{$\xi $}$(b) на одной из жидких границ для зашумленных данных наблюдений. Функционал стоимости (V.2)
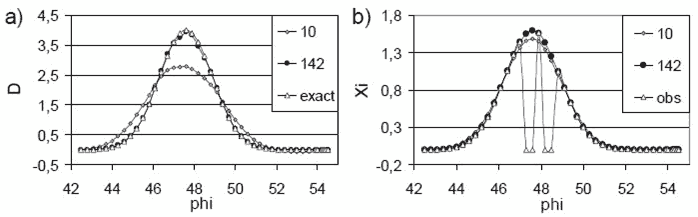
Рис. V.7. Итерационное восстановление функций $\textit{d}$(а) и $\textit{$\xi $}$(b) на одной из жидких границ для данных наблюдений с пропусками. Функционал стоимости (V.2)
Основные публикации:
- Karepova E. D., Shaidurov V. V.
A parallel implementation of FEM for a boundary value problem for the shallow water equations // Notes on Numerical Fluid Mechanics and Multidisciplinary Design. — 2011. — V. 115. — P. 29-42. - Karepova E., Shaidurov V., Dementyeva E.
The numerical solution of data assimilation problem for shallow water equations // Int. J. of Num. Analysis and Modeling, Series B. — 2011. — V. 2 (2-3). — P. 167–182 . - Karepova E., Dementyeva E.
Solution of Assimilation Observation Data Problem for Shallow Water Equations for SMP-Nodes Cluster // Lecture Notes in Computer Science. — 2011. — V. 6873. — P. 444–451 . - Дементьева Е. В., Карепова Е. Д., Малышев А. В.
Эффективность численного моделирования на кластерных системах распространения поверхностных волн // Вестник НГУ, Серия: информационные технологии. — 2011. — Т. 9. — Вып. 1. — С. 11-20.
(Отдел вычислительной математики)
| К началу | |
Проект № 40. «Термодинамические согласованные модели сплошных сред и их вычислительное моделирование: вычислительные модели, алгоритмы и их программная реализация; новые критерии устойчивости движения, позволяющие указывать допуски на определяющие параметры»
Руководитель проекта: академик РАН С. К. Годунов
Ответственный исполнитель от ИВМ СО РАН: д.ф.-м.н., проф. В. М. Садовский
Исполнители: М. П. Варыгина, О. В. Садовская, А. Н. Красненко
В 2011 г. в рамках завершаемого проекта были разработаны параллельные алгоритмы и программы для численного решения динамических задач на основе уравнений редуцированной модели упругой среды с микроструктурой. Эти уравнения строятся путем упрощения уравнений моментной теории упругости Коссера. В них учитывается вращение частиц микроструктуры материала, которое происходит за счет несимметрии тензора напряжений, но моментные напряжения отсутствуют. Существенное упрощение состоит в том, что упругие свойства материала характеризуются не шестью, а тремя феноменологическими параметрами. Расчеты показали, что редуцированная модель менее интересна, чем полная, поскольку она не описывает явления резонанса на собственной частоте вращательного движения частиц, однако она может быть использована в расчетах волновой динамики структур типа жидких кристаллов, имеющих широкое практическое применение. На рис. V.8 приведены результаты численного решения задачи о распространении поверхностной волны в рамках редуцированной модели, полученные для сопоставления с известным точным решением.
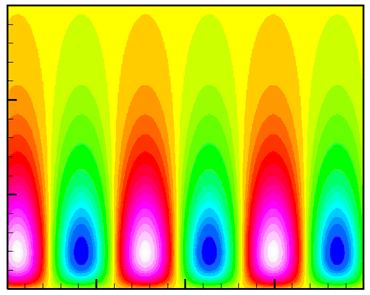
Рис. V.8. Линии уровня касательного напряжения в задаче о распространении поверхностной волны, полученные на основе редуцированной модели
На основе предложенной ранее математической модели для описания течений сыпучей среды, учитывающей образование застойных зон в движущемся потоке, выполнено численное решение задачи о неоднородном сдвиге. Разработан вычислительный алгоритм для исследования одномерных решений нелинейной системы уравнений, в рамках которой движение разрыхленной сыпучей среды описывается как вязкое течение, а в зонах уплотнения учитываются упругие деформации частиц. Проведено сравнение нестационарного численного решения задачи о сдвиге, вызванном горизонтальным перемещением тяжелой шероховатой плиты, установленной на поверхности слоя, с точным стационарным решением, полученным в рамках предположения о недеформируемых частицах, которое показало хорошее качественное и количественное соответствие результатов по глубине зоны течения и скорости поверхности среды (рис. V.9).
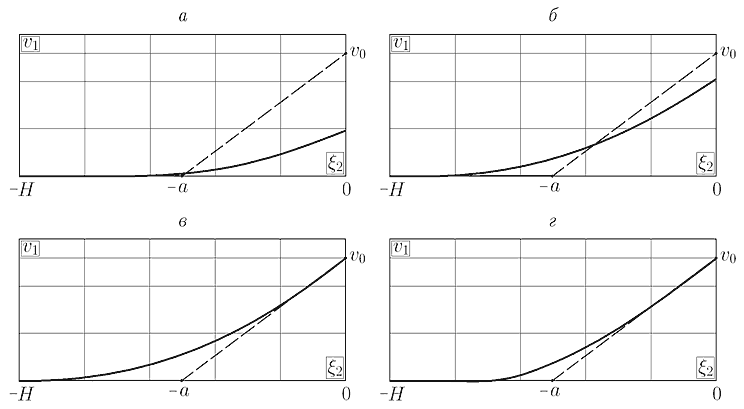
Рис. V.9. Профиль горизонтальной скорости по глубине слоя в различные моменты времени (сплошная линия — численное решение, штриховая линия — точное решение)
С помощью разработанного ранее комплекса параллельных программ на кластерах ИВМ СО РАН и МСЦ РАН проведена большая серия методических расчетов косого соударения пластин в упругой и упругопластической постановке, результаты которых продемонстрировали влияние вращательного движения частиц в точке контакта на механизм волнообразования сварного шва.
Основные публикации:
- Красненко А. Н., Садовская О. В.
Математическое моделирование сдвиговых течений сыпучей среды с застойными зонами // Тр. всерос. науч. конф. «Фундаментальные и прикладные вопросы механики и процессов управления». — Владивосток: ИАПУ ДВО РАН. — 2011. — С. 91-96. - Садовская О. В.
Моделирование динамического контактного взаимодействия упругопластических тел с использованием высокопроизводительных вычислений // Математические и информационные технологии (MIT-2011) [Электронный ресурс] / Междунар. конф. (IX конференция «Вычислительные и информационные технологии в науке, технике и образовании»), Врнячка Баня, Сербия, 27-31 августа 2011 г., Будва, Черногория, 31 августа — 5 сентября 2011 г., № гос. регистрации — 0321102644, Режим доступа: http://conf.nsc.ru/MIT-2011/reportview/48869, свободный. — Загл. с экрана (дата обращения: 15.11.2011). — 6 p. - Садовский В. М.
Математические модели структурно-неоднородных сред и их численная реализация на многопроцессорных системах // Математические и информационные технологии (MIT-2011) [Электронный ресурс] / Междунар. конф. (IX конф. «Вычислительные и информационные технологии в науке, технике и образовании»), Врнячка Баня, Сербия, 27-31 августа 2011 г., Будва, Черногория, 31 августа — 5 сентября 2011 г., № гос. регистрации — 0321102644, Режим доступа: http://conf.nsc.ru/MIT-2011/reportview/48868, свободный. — Загл. с экрана (дата обращения: 15.11.2011). — 6 p.
(Отдел вычислительной механики деформируемых сред)
| К началу | |
Проект № 50. «Модели изменения биосферы на основе баланса углерода (по натурным и спутниковым данным и с учетом вклада бореальных экосистем)»
Руководители проекта: академик РАН Е. А. Ваганов, член-корреспондент РАН А. М. Федотов
Ответственный исполнитель от ИВМ СО РАН: д.ф.-м.н., проф. В. М. Белолипецкий
Исполнитель: П. В. Белолипецкий
Ряд независимых исследований говорят о том, что наблюдается большой сток атмосферного СО2 в континентальные экосистемы умеренных широт северного полушария. Вывод базируется на анализе пространственного распределения концентрации СО2, интерпретации глобальной базы данных o изотопах в атмосферном углекислом газе, измерениях отношения O2/N2 в атмосфере, прямых наблюдениях поглощения CO2 многими лесными экосистемами в Европе и Северной Америке, и измерениях накопления углерода в наземных экосистемах. Тем не менее, до сих пор непонятно какие именно континентальные экосистемы поглощают углерод и какие процессы дают существенный вклад в поглощение углерода. Обратные модели, которые разделяют континентальный сток между частями северного полушария, дают большой разброс оценок: очень большой разброс по Европе (от −0.9 до +0.2 ГтС год−1) и Северной Азии (от −1.2 до +0.3 ГтС год−1) и большой разброс по Северной Америке (от −0.6 до −1.1 ГтС год−1).
Прямые измерения потоков CO2 между атмосферой и биосферой с помощью метода микровихревых пульсаций (eddy covariance) проводились на множестве пунктов по всему миру. Эти исследования оценивают потоки на достаточно малых пространственных масштабах (обычно несколько гектаров). И трудной задачей является экстраполяция результатов на большие регионы.
Концентрации CO2, измеряемые на высокой вышке (более 200 м), являются результатом перемешивания на области порядка 104 км2. Эти концентрации дают потенциальную возможность оценки потоков углерода над большим регионом, где локальные неоднородности потоков сглаживаются.
Рассматриваются процессы, которые влияют на баланс CO2 в атмосфере на месячном и сезонном временных масштабах. Горизонтальные градиенты концентрации CO2 (в 1-5 ppm) формируются на масштабах в сотни км. А различие концентраций (в 5-10 ppm) между атмосферным пограничным слоем (АПС) высотой 1-2 км и смешанным слоем тропосферы (до 10 км) составляет 5-10 ppm. Смешанный слой тропосферы является большим резервуаром СО2, концентрация в котором меняется медленно (в сравнении с АПС). Поэтому среднемесячные концентрации определяются в основном вертикальным обменом. Предлагаемый метод основывается на том, что концентрации CO2 в пограничном слое определяются в основном обменами с поверхностью и со смешанным слоем тропосферы. Причём среднемесячный обмен с тропосферой пропорционален разности между концентрациями CO2 в пограничном слое (до 2 км) и в смешанном слое тропосферы (2-10 км). Средняя концентрация CO2 в пограничном слое определяется на основе измерений вышки. Концентрация CO2 в свободной тропосфере не сильно отличается для одного периода года и одной широты при разных местах измерения (полёты на самолёте, измерения на высокой скале). Для определения вертикального обмена используются вертикальные скорости из данных реанализа, например NCEP Reanalysis model .
Предлагается метод для определения потока СО2 ($Q_{C}$), использующий точечную модель для концентраций углекислого газа в атмосфере и измеренные на высоких вышках профили концентраций в атмосфере. Показано, что для оценки потока достаточны данные измерений концентраций СО2 на уровне вышки. Выполнен анализ данных измерений концентраций СО2 на вышке, взятых с сервера ftp://ftp.cmdl.noaa.gov/ccg/towers/.
Можно считать, что в перемешанном слое $H\le z\le H_{K} $ средняя концентрация $C=C(t,H)=C_{H} (t)$, где $C_{H} (t)$ — концентрация на уровне вышки. Для оценки потока $\textit{Q${}_{C}$}$ получается упрощенная формула
\[Q_{C} ^{упрощ} =Q_{CH} +H_{K} \frac{dC_{H} }{dt} .\]
Обмен между нижним и верхним слоями атмосферы QCH оценивается по формуле
\[\hat{Q}_{CH} =\alpha (\hat{C}_{H} -C_{тр} ),\]
где $\textit{$\alpha $}$ — скорость массообмена в верхних слоях тропосферы, $\hat{C}_{H} =\frac{1}{T} \int _{0}^{T}C_{H} dt $ — средняя концентрация СО${}_{2}$ на интервале [0,T], С${}_{тр}$ — концентрация СО${}_{2}$ в верхних слоях тропосферы.
Коэффициент $\alpha $ определяется для рассматриваемой вышки по данным реанализа.
Летом в основном $C_{H} < C_{тр} $ и $Q_{CH} < 0;$ зимой $C_{H} > C_{тр} $ и $Q_{CH} > 0.$ Значения С${}_{тр}$ определялись по значениям $C_{H} $. Для «летнего» периода $C_{тр} \ge C_{H\max } $, для «зимнего» периода $C_{тр} \le C_{H\min}$.
На рис. V.10 представлены измеренные вертикальные профили для типичных летних суток. Ночью (3:00) наблюдается поток CO2 с поверхности вследствие дыхания. Выделяемый углекислый газ сконцентрирован около поверхности из-за слабого вертикального перемешивания. До восхода (9:00) концентрация растёт в приповерхностных слоях. Днем воздух около поверхности становится теплее, чем в верхнем слое, формируется неустойчивая стратификация и воздух начинает перемешиваться за счёт конвекции. В течение дня высота конвективного слоя растёт (12:00). Затем (15:00 и 21:00) высота смешанного конвекцией слоя становится выше высоты вышки. В этот период в перемешанном конвективном слое концентрации на всех высотах практически равны, поэтому для оценки потока СО2 вблизи поверхности земли можно использовать измеренные значения концентраций СО2 на высоте вышки в вечернее время.
Примеры расчетов и анализ полученных результатов. В качестве исходной информации для оценки потока углерода использовали базу данных измерений концентраций СО2 на вышке с координатами 45° северной широты и 90° восточной долготы.
Показано, что в летнее время осуществляется сток СО2 из атмосферы, а переход от стока углерода к эмиссии происходит для этой местности в конце сентября — начале октября.
Рассчитаем суммарные потоки $\hat{Q}_{C}$ за «летний» и «зимний» периоды: $\stackrel{\frown}{Q}_{C} ^{летний} \approx -185.4{\raise0.7ex\hbox{$ г\cdot C $}\!\mathord{\left/ {\vphantom {3\cdot ! м^{2} \cdot лето}} \right.}\!\lower0.7ex\hbox{$ м^{2} \cdot лето $}}$, объем эмиссии углерода в течение холодного сезона составляет $\stackrel{\frown}{Q}_{C} ^{зимний} \approx {\rm 1}26.9$${\raise0.7ex\hbox{$ г\cdot C $}\!\mathord{\left/ {\vphantom {3\cdot ! м^{2} \cdot лето}} \right.}\!\lower0.7ex\hbox{$ м^{2} \cdot зима $}}$, отсюда общий годовой баланс углерода $\stackrel{\frown}{Q}_{C} ^{годовой} \approx -58.5 {\raise0.7ex\hbox{$ г\cdot C $}\!\mathord{\left/ {\vphantom {3\cdot ! м^{2} \cdot год}} \right.}\!\lower0.7ex\hbox{$ м^{2} \cdot год $}}$.
Итак, суммарный годовой поток отрицательный, т.е. в данном регионе преобладает поглощение углерода наземными экосистемами.
Предложен способ оценки потока углерода вблизи поверхности земли с использованием точечной модели и измеренных на вышке вертикальных распределений концентраций СО2. Выполнены расчеты для измерений на высоте 396 м и на высоте 244 м. Так как результаты отличаются незначительно, то можно применять предлагаемый метод и для вышек меньшей высоты. Показано, что в балансе углерода рассмотренного региона поглощение наземными экосистемами преобладает над эмиссией.
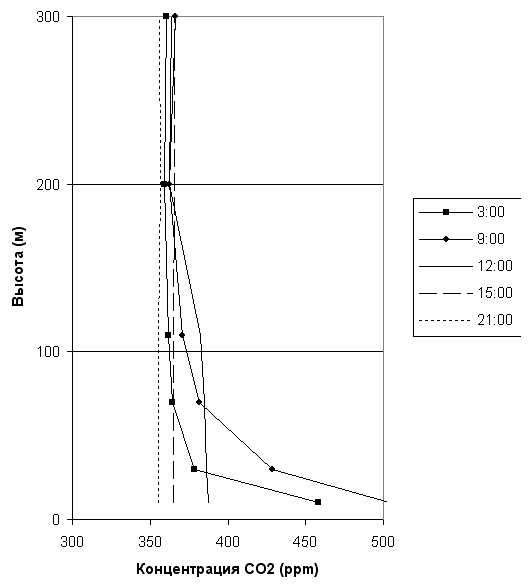
Рис. V.10. Вертикальные распределения концентрации СО2 в летний период
Основные публикации:
- Белолипецкий В. М., Белолипецкий П. В.
Оценка потока углерода между атмосферой и наземной экосистемой по измеренным на вышке вертикальным распределениям СО2 // Вестник НГУ. — 2011. — Т. 9. — Вып. 1. — С. 75-81.
(Отдел вычислительных моделей в гидрофизике)
| К началу | |
Проект № 65. «Теоретико-групповые и геометрические методы исследования нелинейных моделей механики сплошных сред и математической физики: точные решения, интегрируемость, сигулярности»
Руководители проекта: академик РАН Л. В. Овсянников, член-корреспондент РАН И. А. Тайманов
Блок: Исследование инвариантных подмоделей неклассических уравнений конвекции
Ответственный исполнитель от ИВМ СО РАН: д.ф.-м.н., проф. В. К. Андреев
Исполнители: В. Б. Бекежанова, Н. Л. Собачкина, И. В. Степанова
1. Дан анализ решения уравнений термодиффузии вида
\[u=0,\, \, \, \, \, \, v=0,\, \, \, \, \, \, w=w(r,t),\, \, \, \, \, \, p=-\rho f(t)z+D(t),\, \, \, \, \, \, \theta =Az+T(r,t),\, \, \, \, \, \, \, c=Bz+K(r,t),\]
которое применяется для описания однонаправленного движения бинарной смеси в вязкой теплопроводной жидкости, причем смесь занимает область в виде круглой цилиндрической струи радиусом $\textit{a}$. Пусть $w_{j} (r,t)$ — осевые скорости смеси и жидкости ($j=1,2$), $p_{j} =-\rho _{j} f_{j} (t)z+D_{j} (t)$ — их давления, $\theta _{j} =A_{j} z+T_{j} (r,t)$ — распределения температур, $c_{1} =B_{1} z+K(r,t)$ — распределение концентрации в смеси. Предположим, что коэффициент поверхностного натяжения на границе раздела $r=a$ линейно зависит от температуры и концентрации $\sigma (\theta, c)=\sigma _{0} -\sigma _{\theta } (\theta -\theta _{0} )-\sigma _{c} (c-c_{0} ),$ где $\sigma _{\theta } >0$ — температурный коэффициент, $\sigma _{c} $ — концентрационный коэффициент (обычно $\sigma _{c} <0,$ поскольку поверхностное натяжение увеличивается с ростом концентрации), $\theta _{0}, $ $c_{0} $ — некоторые постоянные средние значения. Для функций $w_{j}, \, \, T_{j}, \, \, K$ возникает сопряженная начально-краевая задача, которая решена методом преобразования Лапласа. Доказано, что с ростом времени скорости в струе и в окружающей жидкости становятся постоянными.
2. Построено инвариантное решение, описывающее стационарное течение смеси в плоском вертикальном слое, ограниченном твердыми стенками, на которых поддерживается постоянная температура. Плотность определяется зависимостью $F=c-D_{T} /(\chi -D)T+f(D_{T} /(\chi -D)T)$, где $f$ — произвольная функция своего аргумента. Скорость имеет только вертикальную составляющую, которая зависит от горизонтальной координаты. В слое предполагается наличие постоянного градиента концентрации в вертикальном направлении.
На рис. V.11 представлены профили скорости и плотности смеси для силы плавучести, зависящей от температуры по квадратичному закону:$f=T_{0} (D_{T} /(\chi -D)T))^{2} +T_{1}, $ где $T_{0}, \, \, T_{1} $ — постоянные. Конвективное течение состоит из трех частей разной интенсивности: вблизи стенок жидкость опускается вниз, а в центре слоя поднимается вверх, что соответствует большим у стенок и малым в центре значениям плотности. Такой профиль скорости отличается от профиля, полученного ранее различными авторами для линейной зависимости силы плавучести от температуры, тем самым нелинейное распределение плотности существенно влияет на распределение скорости смеси.
Полученные результаты могут использоваться для уточнения математической модели конвективного движения под действием силы плавучести и эффекта Соре, а также для вычисления коэффициента термодиффузии в термогравитационных колоннах или других установках.
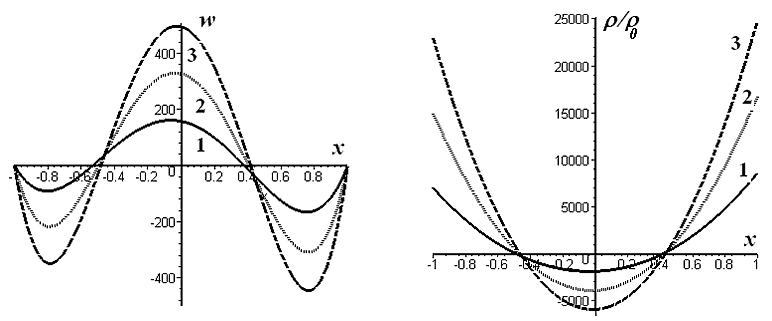
Рис. V.11. Профили скорости (слева) и плотности (справа). Кривая 1 соответствует $T_{0} $= 100, кривая 2 — $T_{0}$ = 200, кривая 3 — $T_{0}$ = 300
3. Изучена задача о совместном стационарном течении двух вязких теплопроводных жидкостей в плоском слое в условиях микрогравитации. Система ограничена твердыми стенками, одна из которых может двигаться с постоянной скоростью. На внешних границах задано линейное распределение температур. Вдоль границы раздела действуют касательные силы, причем поверхностное натяжение линейно зависит от температуры. Меняя скорость движения стенки, градиенты давления и температуры, можно получать различные режимы течений. Задавая скорость движения стенки специальным образом, можно добиться нулевого объемного расхода во втором слое. Такой режим течения есть суперпозиция термокапиллярного течения, порожденного наличием продольного градиента температуры, сдвигового течения, когда жидкость увлекается подвижной границей, и вынужденного течения, обусловленного продольным градиентом давления, и описывается решением типа Остроумова — Бириха.
Методом линеаризации исследована устойчивость указанного течения. Найдено асимптотическое поведение комплексного декремента в длинноволновой области для недеформируемой поверхности раздела. Получены аналитические представления собственных функций в случае плоских возмущений.
Каждая из компонент такого комбинированного течения становится неустойчивой за счет различных механизмов. С изменением градиентов давления и температуры, скорости движения стенки интенсивность движения увеличивается и происходит деформация формы профиля скорости (рис. V.12).
Имеется зависимость характеристик устойчивости от направления прокачки ($\bar{a}$ — безразмерный градиент давления), градиента температуры (Ma$\textit{ — }$число Марангони, отрицательным значениям соответствует случай, когда направление градиента температуры противоположно направлению продольной оси), движения стенки (Re$\textit{ — }$число Рейнольдса, отрицательным значениям соответствует случай, когда направление движения стенки противоположно направлению продольной оси) и толщин слоев ($h_{1}, \, \, h_{2}, \, \, h=h_{1} /h_{2} $).
При малых толщинах слоев ($h_{1}, \, \, h_{2} <1$) наиболее опасными являются тепловые моды (рис. V.13). Кризис вызывается волнами, которые распространяются в направлении прокачки. Для слоев, толщины которых $h_{1}, \, \, h_{2} >1,$ имеет место вырождение волновых мод при небольших числах Рейнольдса и малых расходах жидкости (см. вставку на рис. V.13, $\textit{б}$).
При малых числах $\textit{$Re_{*} $}$ в условиях, когда $h_{1}, \, \, h_{2} <1$ и $h<1$, во всех случаях, когда направление движения стенки и направление продольного градиента температуры противоположны, течение стабилизируется.
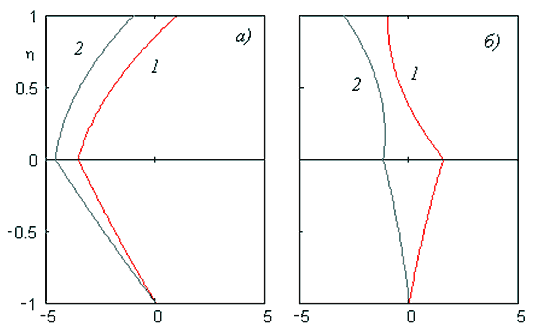
Рис. V.12. Безразмерное распределение скорости жидкостей в слоях при изменении $\bar{a}$, Ma, Re:
$\textit{а) }$$\bar{a}=1.461\cdot 10^{4}, \, $ $\, {\rm Ma}=2.792\cdot 10^{5}, \, $$\textit{1 — $Re=5.405\cdot 10^{3} $, 2 — $Re=-5.405\cdot 10^{3} $}$;
$\textit{б) 1 — }\bar{a}=1.461\cdot 10^{4} $, ${\rm Ma}=-4.188\cdot 10^{5}, \, $$\textit{$Re=-5.405\cdot 10^{3} $}$,$\textit{ 2 — }\bar{a}=-1.461\cdot 10^{4} $, ${\rm Ma}=1.396\cdot 10^{5}, \, $ $\textit{$Re=-1.622\cdot 10^{4} $}$
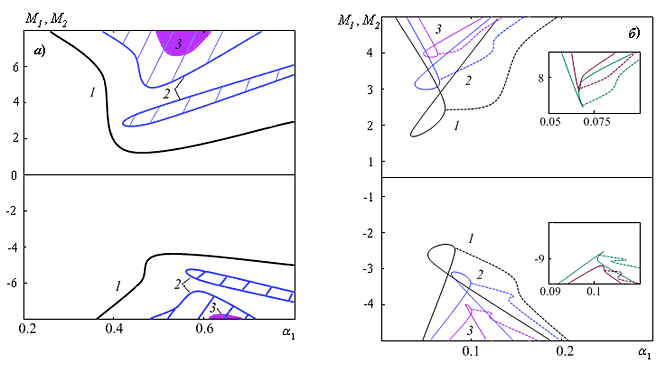
Рис. V.13. Нейтральные кривые $\textit{а)}$ — гидродинамические моды: $\textit{1-3 — $Re_{*} =300,\, \, 100,\, \, 10$}$, $M_{1} ={\rm Ma}\cdot 10,$ $M_{2} ={\rm Ma}\cdot 10^{2} $ при $\textit{$Re_{*} =\, 10$}$; $\textit{б)}$ — тепловые моды при $\textit{$Re_{*} =\, 100$}$: $\textit{1-3 — $h=1,\, \, 10,\, \, 50$}$, $M_{1} ={\rm Ma}\cdot 10^{2}, $ $M_{2} ={\rm Ma}\cdot 10^{3} $ при $\textit{$h=50$.}$ На вставке $\textit{$Re_{*} =\, 10$}$, $\textit{$h=\, \, 10,\, \, 50$}$
4. Исследована задача о конвективном течении вязкой теплопроводной жидкости в условиях радиационного нагрева применительно к глубоководным пресным водоемам. В качестве уравнения состояния жидкости использовалась квадратичная зависимость плотности $\rho $ от температуры $\theta $: $\rho =\rho _{0} [1-\alpha (\theta -\theta _{0} )^{2} ]$. В случае объемного поглощения (проникновения солнечной радиации в среду) мощность тепловых источников $F_{w} (z)=\sigma {\rm \hbox{æ} }R\, \exp (-{\rm \hbox{æ} }z)$ определяется параметрами: $\sigma $ — отношение интенсивности солнечной радиации к радиационному балансу $\textit{R}$ на поверхности воды, ${\rm \hbox{æ} }$ — показатель ослабления солнечной радиации в воде (показатель поглощения) и учитывается в уравнении энергии.
Доказано, что всегда существует стационарное течение в цилиндре большого радиуса вида
\[u=(u,v,w),\, \, \, \, \, \, u=u(z)r,\, \, \, \, \, \, v=0,\, \, \, \, \, \, w=w(z),\, \, \, \, \, \, p=p(z)+\frac{a_{1} }{2} r^{2} ,\, \, \, \, \, \, \theta =\theta (z)\, ,\]
гдe $u$ — радиальная компонента скорости, $\textit{v}$ — азимутальная, $\textit{w}$ — осевая, $\textit{p}$ — давление, параметр $a_{1} $ подлежит определению. Это решение зависит от безразмерных параметров: $a={a_{1} l^{4} \mathord{\left/ {\vphantom {a_{1} l^{4} \nu ^{2} }} \right.} \nu ^{2} } $, ${\rm Ga}=gl^{3} /\nu ^{2} $ — число Галилея, ${\rm Gr}=g\alpha \theta _{0}^{2} l^{3} /\nu ^{2} $ — число Грасгофа, $\Pr =\nu /\chi $ — число Прандтля, $f_{1} =\sigma \, {\rm \hbox{æ} R}l^{2} /k\theta _{0} $ — параметр тепловыделения.
Задача на функцию $u(z)$ и параметр $a$ отделяется и является сильно нелинейной. Предложена итерационная процедура для определения параметра $a$ и построения радиальной компоненты скорости. Далее последовательно решаются задачи для функций $w(z),\, \, \theta (z),\, \, p(r,z)$, где $\textit{p}$ — отклонение от гидростатического давления. Для входных данных, использующих средние значения физических параметров задачи (поток тепла, глубина, радиационный баланс и пр.), найдены три различных значения параметра $a$: $a^{1} $= 12.0168, $a^{2} $$=9.12\cdot 10^{-7}$ и $a^{3}=7.341\cdot 10^{-6}$. Таким образом, численные расчеты в широком диапазоне параметров дают три различных стационарных течения. Графики функций $u(z)$ и $w(z)$ приводятся на рис. V.14.
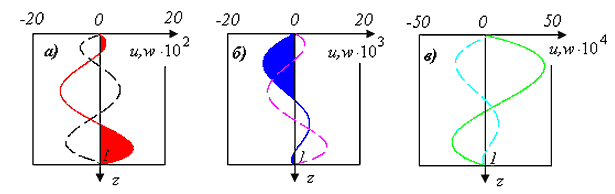
Рис. V.14. Зависимость радиальной ($u$, сплошная линия) и осевой ($w$, штриховая линия) компонент от $z$: $\textit{а) }$$a^{1} =12.0168$; $\textit{б) }$$a^{2} $$=9.12\cdot 10^{-7} $; $\textit{в) }$$a^{3} =-7.341\cdot 10^{-6} $
Значение $\textit{a}$${}^{1}$, по-видимому, не является физичным, поскольку при таком значении параметра давление должно существенно расти в радиальном направлении.
Исследована устойчивость всех трех классов решений относительно малых возмущений (рис. V.15). На нейтральных кривых имеются 2 моды неустойчивости. Кривые 1 и 3 на рис. V.15 соответствуют наиболее опасной моде, в этом случае неустойчивость связана с развитием тепловых волн. Кривые 2 и 4 — гидродинамические моды, кризис связан с нарастанием гидродинамических возмущений. При отрицательном значении $a=a^{3} $ течение состоит из двух встречных потоков, нейтральные кривые имеют вид 5, б) и гидродинамическая неустойчивость проявляется в виде медленно дрейфующих вихрей на границе встречных потоков. При положительных значениях $a=a^{1}, \, \, a^{2} $ в основном течении появляются дополнительные потоки (на рис. V.14 выделены закрашенными областями) и происходит перестройка нейтральных кривых. Ветви нейтральных кривых соединяются через замкнутую петлю (на рис. V/15 закрашенные области), при этом оба механизма неустойчивости имеют место.
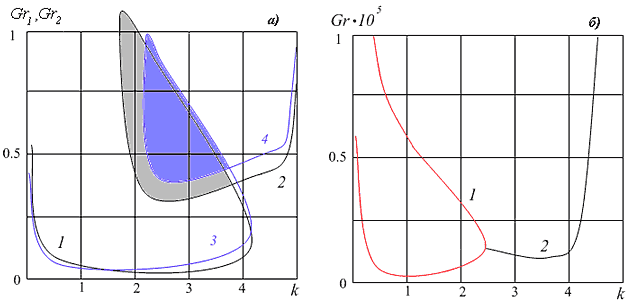
Рис. V.15. Нейтральные кривые ${\rm Gr}(k)$: $\textit{а) }$кривые $\textit{1, 2 — }$$a^{1} =12.0168$, ${\rm Gr}_{1} ={\rm Gr}\cdot 10^{5} $, $\textit{3, 4 — }$$a^{2} =9.12\cdot 10^{-7} $, ${\rm Gr}_{2} ={\rm Gr}\cdot 10^{5} $; $\textit{б)}$ $a^{3} =-7.341\cdot 10^{-6} $
Таким образом, построено точное решение, описывающее восходящее стационарное течение в водоеме или большом резервуаре и исследована его устойчивость
5. Дано обобщение неравенства Фридрихса для областей, состоящих из трех отрезков. Определена минимальная положительная постоянная $\textit{M}$, входящая в правую часть неравенства. Она является решением трансцендентного уравнения и зависит от физических параметров жидкости и длин отрезков. Неравенство имеет вид
\[\int _{-l_{1} }^{0}u_{1}^{2} (y)\, dy+ \int _{0}^{l_{2} }u_{2}^{2} (y)\, dy+ \int _{l_{2} }^{l_{3} }u_{3}^{2} (y)\, dy\le M\left(\mu _{1} \int _{-l_{1} }^{0}u_{1y}^{2} (y)\, dy+ \mu _{2} \int _{0}^{l_{2} }u_{2y}^{2} (y)\, dy+ \mu _{3} \int _{l_{2} }^{l_{3} }u_{3y}^{2} (y)\, dy \right),\]
где $\mu _{1} $, $\mu _{2} $, $\mu _{3} $ — динамические вязкости жидкостей, а функции $u_{1} $, $u_{2} $, $u_{3} $ удовлетворяют условиям сопряжения при $y=0,\, $ $y=l_{2}, $ причем $u_{1} (-l_{1} )=u_{3} (l_{3} )=0.$ С помощью доказанного неравенства удалось получить априорные оценки для скоростей совместного нестационарного движения трех жидкостей в плоских слоях.
Основные публикации:
- Андреев В. К., Бекежанова В. Б.
О малых возмущениях термокапиллярного стационарного двухслойного течения в плоском слое с подвижной границей // Журнал СФУ. Серия: математика и физика. — 2011. — № 4(4). — С. 434–444 . - Андреев В. К., Собачкина Н. Л.
О движении затопленной струи бинарной смеси в вязкой жидкости // Журнал СФУ. Серия: математика и физика. — 2011. — № 4(3). — С. 308–319 . - Андреев В. К., Степанова И. В.
Об одном конвективном течении бинарной смеси в вертикальном слое // Сибирский журнал индустриальной математики. — 2011. — Т. 14. — № 1(45). — С. 17-26. - Бекежанова В. Б.
О смене форм неустойчивости стационарного течения двухслойной жидкости в наклонном канале // МЖГ. — 2011. — № 4. — С. 24-34. - Бекежанова В. Б. Андреев В. К.
Об однонаправленном двухслойном течении в условиях микрогравитации // Вестник Нижегородского ун-та им. Н. И. Лобачевского. — 2001. — № 4(3). — С. 639–640 . - Лемешкова Е. Н.
О неравенстве Фридрихса для области, состоящей из трех отрезков // Материалы 64 научной конф. «Герценовские чтения — 2011». СПб: РГПУ им. А. И. Герцена, 2011. С. 80-84. - Степанова И. В.
О конвективном вихревом течении вязкой жидкости // Сб. докл. Всерос. науч. конф. «Фундаментальные и прикладные вопросы механики и процессов управления» (электронный ресурс). Владивосток: ИАПУ ДВО РАН. — 2011. — С. 295–297 . - Степанова И. В.
О конвекции бинарной смеси в вертикальном слое под действием эффекта Соре при нелинейной силе плавучести // Вестник Нижегородского ун-та им. Н. И. Лобачевского. — 2011. — № 4(3). — С. 1135–113 6. - Степанова И. В.
Об одном инвариантном решении уравнений термодиффузии с нелинейной силой плавучести // ПММ. (В печати).
(Отдел дифференциальных уравнений механики)
| К началу | |
Проект № 95. «Комплексные исследования механизмов стратификации биологических, химических и физических компонент водных экосистем как основа для прогноза и управления качеством воды»
Руководитель проекта: член-корреспондент РАН А. Г. Дегерменджи
Ответственный исполнитель от ИВМ СО РАН: д.ф.-м.н., проф. В. М. Белолипецкий
Исполнители: П. В. Белолипецкий, С. Н. Генова, Л. А. Компаниец, О. С. Питальская
Выполнены пробные измерения компонент скоростей течений воды в озере Шира с помощью акустических доплеровских профилографов течений ADCP 600 и 1200 кГц (Teledyne RD Instruments, USA), способных определять трехмерную скорость вдоль всего столба жидкости на глубину до 14 м (ADCP 1200) или до 60 м (ADCP 600). Проводились также измерения трех компонентов скорости течений в точке с помощью акустического доплеровского профилографа 16МГЦ ADV (SonTek, USA).
Как показывает опыт исследования гидрофизического режима озера Шира, каждый из методов в цепочке (математическая модель, численный эксперимент, натурный эксперимент) имеет свои преимущества и недостатки одновременно. Аналитические решения позволяют найти решение (скорости течения) в каждой точке пространства, но могут быть получены, как правило, только в очень частных случаях. Если прибавить к этому тот факт, что при нахождении аналитических решений используются очень важные, но сложно измеряемые величины, такие, как коэффициенты вертикального и горизонтального обмена, то становится понятно, что делать выводы только на основе аналитических решений необдуманно. В задачах гидрофизики озер широко применяются численные модели. Однако для нестационарных задач трудно определить нестационарные входные параметры задачи.
Казалось, что измерения скорости течения с помощью приборов нового поколения ADCP и SonTek способны решить эту задачу, если бы не ряд проблем. При изменчивой и сильно нестационарной метеорологической картине в районе озера Шира в летний период (ветер меняется в зависимости от положения точки на озере, сильные волны) сам процесс измерения становится сложным, также как и интерпретация полученных данных. Измерения проводились в отдельных точках, что затрудняет восстановление картины течения в целом. Поэтому для выяснения картины течения в озере Шира необходимы совместные теоретические и экспериментальные исследования (комплексный подход).
В рамках этого комплексного подхода получены следующие результаты.
- Найдено аналитическое решение для стационарного движения неоднородной жидкости (простейшая модель для дрейфовой составляющей модели Экмана, распределение температуры по глубине моделирует термоклин, уравнение состояния равномерно соленой воды). Рис. V.16-V.17 (восточная и северная составляющие горизонтальной скорости, ветер западный 5 м/с ) иллюстрируют картину распределения скорости по глубине, в соответствии с которой одна (две скорости) меняют знак при распределении по глубине. Эти результаты согласуются с результатами измерений. На рис. V.18-V.19 представлены результаты измерений 04.07.2010: координаты точки — широта 54.30.318', долгота 90.13.680', ветер ю-з 2 м/сек с порывами до 3.7 м/сек; потом ветер стих.
- Получены результаты численного моделирования трехмерного течения в озере Шира с использованием свободно распространяемого программного обеспечения, программ GETM (собственно расчетный блок скоростей) и GOTM (блок расчета коэффициента вертикального турбулентного обмена). На рис. V.20 показано поведение горизонтальной скорости на поверхности бассейна, моделирующего батиметрию озера Шира при западном ветре. Результат получен с помощью программы GETM. На рис. V.21-V.22 показаны распределения горизонтальных скоростей по глубине глубоководной части.
- Обработка данных с ADCP, полученных с 28.06.11 по 29.06.11 в результате длительного измерения (13 часов, прибор стоял на дне в центральной части озера) показывает, что на глубине 12 м (нижняя граница термоклина) сильно колеблется вертикальная скорость.
Осредненные данные (средние за 2 минуты) показаны на рис. V.23. На обоих графиках видны колебания вертикальной скорости с периодом приблизительно 2 часа. Наличие внутренних волн косвенно подтверждается данными, которые представил нам А. Толомеев (ИБФ СО РАН). По его измерениям в соседней точке (расстояние между точкой измерения скорости и точкой измерения температуры составило около 100 м) температура на этой глубине менялась в рассматриваемый период измерений от 1.0° C до 1.5° C. Некоторым разумным связующим звеном между тремя описанными способами исследования может стать измерение скорости с использованием программы «bottom-track», позволяющей учитывать движение лодки. Программное обеспечение закуплено, но пока не задействовано.
Проведенные исследования позволяют разработать план проведения натурных измерений для использования в численной модели течений в стратифицированном водоеме.
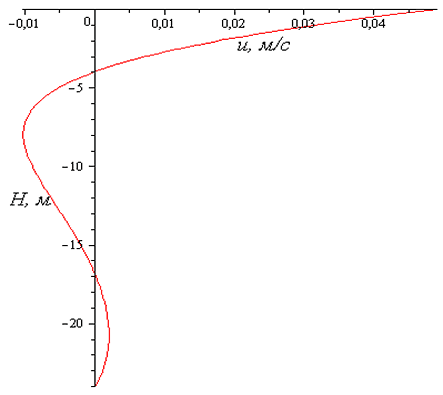
Рис. V.16. Восточная компонента скорости, аналитическое решение
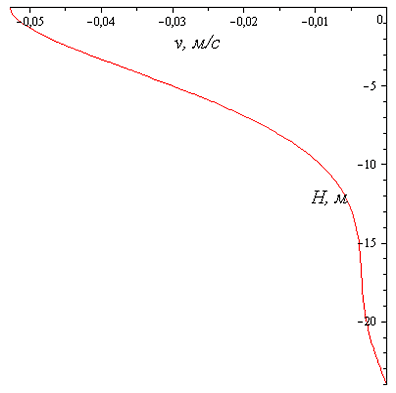
Рис. V.17. Северная компонента скорости, аналитическое решение
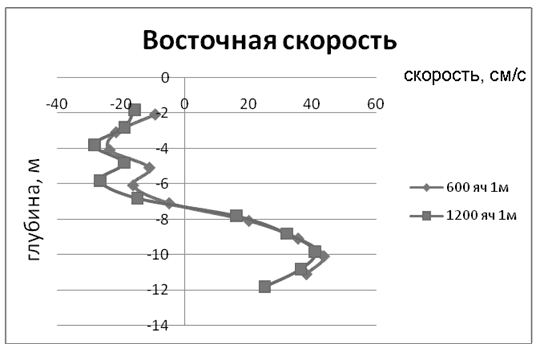
Рис.V.18 Восточная компонента скорости, натурные наблюдения 2010 г.
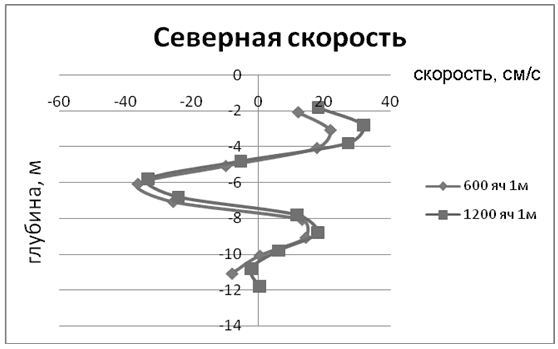
Рис.V.19. Северная компонента скорости, натурные наблюдения 2010 г.
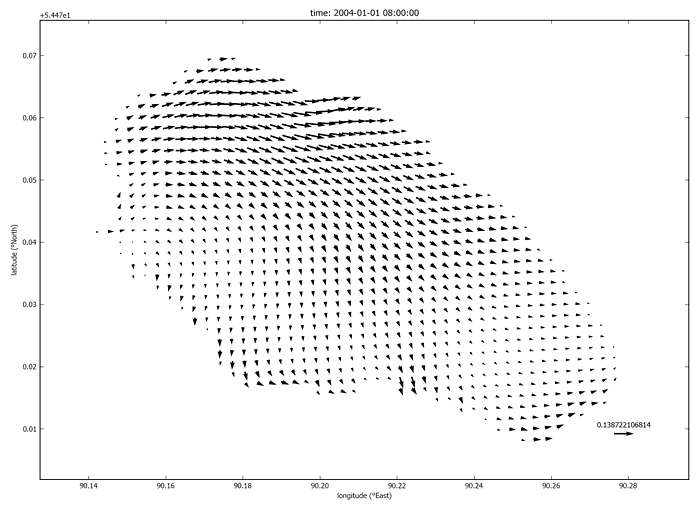
Рис. V.20. Скорости на поверхности озера при западном ветре, численные расчеты
Выполнена модификация одномерной в вертикальном направлении модели для исследования вертикальных распределений температуры и солености воды в мелком озере Шунет. В зимний период по вертикали выделяются слой льда, слой конвективного перемешивания и придонный слой. Для определения динамики толщины ледяного покрова применяется упрощенная модель, основанная на квазистационарном температурном режиме в затвердевшей области. В соленых озерах при образовании льда в результате кристаллизации воды высвобождается соль и формируется слой конвективного перемешивания. Так как в зимний период температура воды мало изменяется по глубине ($T\approx T_{*}$), то плотность воды в основном зависит от солености. Уравнение состояния соленой воды принимается в приближении Буссинеска.
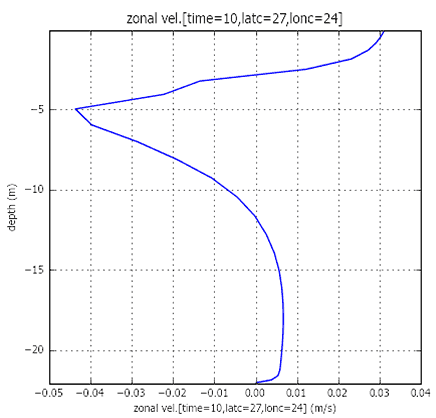
Рис. V.21. Восточная компонента скорости, численные расчеты, глубоководная зона
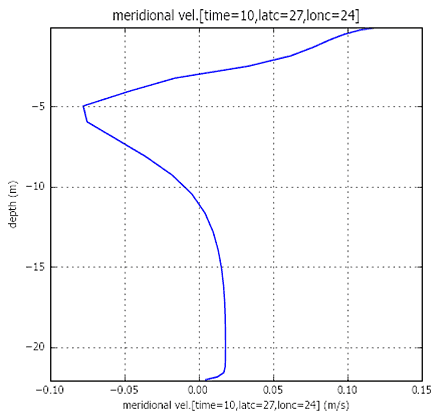
Рис. V.22. Северная компонента скорости, численные расчеты, глубоководная зона
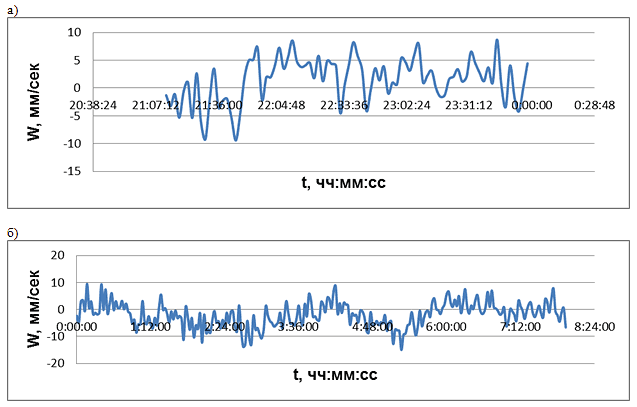
Рис. V.23. Вертикальная компонента скорости, период осреднения 2 мин. а) 28.06.11, б) 29.06.11.
\[\rho =\rho _{0} \left(\varepsilon _{1} +\varepsilon _{2} \frac{T_{*} }{T_{0} } +\varepsilon _{3} \frac{S}{S_{0} } \right)\]
В этом случае толщина слоя конвективного перемешивания не зависит от коэффициента $\varepsilon _{3}$. С учетом этого предположения выведены расчетные формулы для определения глубины распространения конвекции и значений температуры, солености, плотности воды в конвективном слое. Выполнены расчеты вертикальных распределений температуры и солености в озере Шунет, которые хорошо согласуются с натурными данными (рис. V.24).
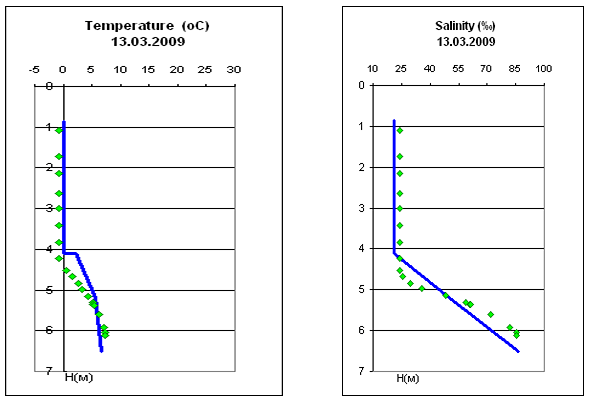
Рис. V.24. Вертикальные распределения температуры и солености в озере Шунет (измеренные — точки, рассчитанные — сплошные линии)
Разработана оригинальная одномерная математическая модель для исследования сезонных вертикальных распределений температуры, солености и плотности воды в озере при различных метеорологических сценариях.
Основные публикации:
- Компаниец Л. А., Якубайлик Т. В., Питальская О. С.
Аналитическое решение одной модели ветрового движения вязкой жидкости (трехмерный случай) // Вычислительные технологии. — 2011. — Т.16. — №3. — С. 50-63.
(Отдел вычислительных моделей в гидрофизике)
| К началу | |
Проект № 116. «Антропогенные риски угледобывающих и нефтегазодобывающих территорий Сибири»
Руководитель проекта: д.т.н., профессор В. В. Москвичев
Ответственный исполнитель от ИВМ СО РАН: д.ф.-м.н., проф. К. В. Симонов
В исследованиях по проекту за 2011 г. приведены результаты уточнения исходной сейсмичности для проектируемой железнодорожной линии трассы «Курагино-Кызыл», основанные на результатах исследования зон возникновения очага землетрясения, инструментального изучения особенностей сейсмического режима, обобщения и корректировки сейсмотектонической модели региона и оценки сейсмической опасности. Представленное информационное, методическое и алгоритмическое обеспечение вычислительной процедуры уточнения исходной сейсмичности УИС железнодорожной трассы «Курагино-Кызыл» позволило выполнить зонирование трассы проектируемой железнодорожной линии по уровню сейсмической опасности (без учета местных грунтовых условий), а также получить численные параметры (магнитуда, расстояние) проектных (модальных) землетрясений для различных по прогнозируемой сотрясаемости участков трассы.
Основные публикации:
- Кобалинский М. В., Перетокин С. А., Сибгатулин В. Г., Симонов К. В.
Социо-экологическая оценка воздействия на природную среду действующих и проектируемых объектов нефтегазового комплекса Красноярского края // Региональная экономика: Теория и практика. — 2011. — Вып. 19. — С. 11-16. - Перетокин С. А., Симонов К. В.
Уточнение исходной сейсмичности на примере трассы железнодорожной дороги «Курагино-Кызыл». // Всерос. конф. с участием иностранных ученых «Проблемы мониторинга окружающей среды» (EM-2011). — Кемерово: КемГУ СО РАН. — 2011. — С. 221–224 . - Кобалинский М. В., Сибгатулин В. Г., Симонов К. В.
Оценка эколого-социальных последствий при реализации крупных инвестиционных проектов // Материалы междунар. конф. «Ресурсная экономика, изменение климата и рациональное природопользование». — Красноярск. — 2011. — P. 20-26.
(Отделы Вычислительных моделей в гидрофизике)
| К началу | |