| ИВМ СО РАН | Поиск |
| Отчеты ИВМ СО РАН |
Отчет ИВМ СО РАН за 2011 год
Проекты СО РАН
- Междисциплинарные интеграционные проекты
- Проекты СО РАН, выполняемые совместно со сторонними научными организациями
- Проект № 89. «Эффективные вычислительные методы на последовательности сеток для решения задач математической физики»
- Проект № 103. «Законы сохранения, инварианты, точные и приближенные решения для уравнений гидродинамического типа и интегральных уравнений»
- Проект № 116. «Моделирование, оптимизация и устойчивость конвективных течений»
- Заказной проект СО РАН
- Программа сибирского отделения РАН «Телекоммуникационные и мультимедийные ресурсы СО РАН»
- Программа сибирского отделения РАН «Высокопроизводительные вычисления СО РАН»
- Экспедиционные проекты СО РАН
- Лаврентьевский грант молодым ученым СО РАН
Проекты СО РАН, выполняемые совместно со сторонними научными организациями
Проект № 89. «Эффективные вычислительные методы на последовательности сеток для решения задач математической физики»
Координаторы проекта: член-корреспондент РАН В. В. Шайдуров; академик КАН Чун Лин (Qun Lin), ИВМиНИР КАН, г. Пекин
Ответственный исполнитель от ИВМ СО РАН: член-корреспондент РАН В. В. Шайдуров
Блок 1. Метод траекторий и метод конечных элементов для уравнений Навье-Стокса для вязкого сжимаемого теплопроводного газа (В. В. Шайдуров, Г. И. Щепановская, М. В. Якубович).
Работа направлена на численное решение системы уравнений Навье-Стокса для вязкого сжимаемого теплопроводного газа. Рассмотрена одномерная по пространству система нестационарных уравнений Навье-Стокса для вязкого теплопроводного газа, которая включает три дифференциальных уравнения в частных производных, вытекающих из законов сохранения массы, количества движения и внутренней энергии газа. Предложенная в работе замена искомых функций в уравнениях неразрывности и внутренней энергии переводит закон сохранения массы и полной энергии из нормы пространства $L_{1}$ в норму гильбертова пространства $L_{2}$. Впоследствии это значительно упрощает обоснование устойчивости и сходимости. Дискретизация по пространству модифицированных уравнений Навье-Стокса осуществляется методом конечных элементов.
Для аппроксимации полной производной по времени каждого уравнения системы используется метод траекторий, который заключается в аппроксимации субстанциональной производной с помощью разностной производной назад по времени вдоль траектории движения частицы. Метод траекторий впервые появился в работах французских и американских ученых для аппроксимации уравнений Навье-Стокса для вязкой несжимаемой жидкости с первым порядком аппроксимации и для одного уравнения переноса массы. В наших исследованиях он применяется к полной системе уравнений Навье-Стокса. Для решения систем алгебраических уравнений используется многосеточный метод с внешними итерациями по нелинейности.
В первой части работы были проведены вычислительные эксперименты для одномерных уравнений Навье-Стокса. И как следует из тестовых расчетов, абсолютная погрешность приближенного решения уменьшается в разы по сравнению с аналогичной погрешностью для немодифицированных уравнений, при этом разностная схема остается первого порядка, редукция которых обеспечивает повышение точности приближенного решения. Для тестирования полученной математической модели функции $u,\, \, \sigma, \, \, \varepsilon $, а также их физические аналоги скорость $u$, плотность $\rho $ и внутренняя энергия $\textit{e}$$e$, задаются явным образом. Нормы погрешности в пространстве $L_{2} $ и $L_{\infty } $ приведены таблицах 1 и 2 для шага по времени $\tau =0.0001$ в момент времени $t=k\tau $ $(k=1000)$.
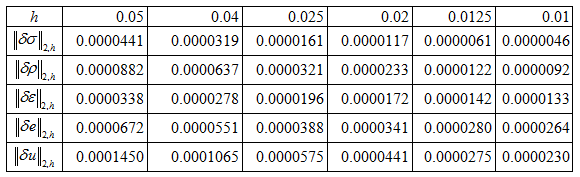
Таблица V.1. Норма погрешности в пространстве $L_{2}$
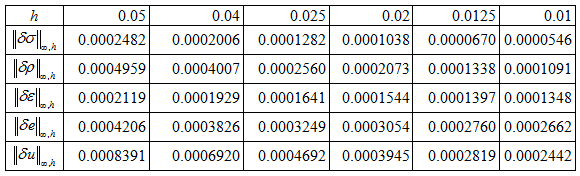
Таблица V.2. Норма погрешности в пространстве $L_{\infty }$
Как следует из тестовых расчетов, абсолютная погрешность приближенного решения уменьшается в разы по сравнению с аналогичной погрешностью для немодифицированных уравнений, при этом разностная схема остается первого порядка. Применение комбинации метода траекторий и метода конечных элементов позволяет построить экономичный алгоритм с вычислительной точки зрения.
В рамках одномерной модели уравнений Навье-Стокса рассмотрена задача о распространении теплового импульса большой мощности в вязком теплопроводном газе, апробированная компьютерная модель используется для изучения одномерных геодинамических процессов.
Блок 2. Численное моделирование течений вязкого сжимаемого теплопроводного газа в канале (В. В. Шайдуров, Г. И. Щепановская, М. В. Якубович).
Работа посвящена математическому и численному моделированию сверхзвуковых течений вязкого теплопроводного газа в трубе и в прямоугольном канале с уступом для различных чисел Маха и чисел Рейнольдса. Используется предложенный выше алгоритм для реализации двумерной модели уравнений Навье-Стокса.
Течение за уступом с твёрдой стенкой. На рисунках V.25 (а, в, д, ж) представлено поле скоростей в канале с уступом, на рисунках V.25 (б, г, е, з) изображены соответствующие изолинии плотности. Расчёты проводились для чисел Маха $M=2\div4$, числа Рейнольдса менялись в диапазоне Re = $2\times$10${}^{3}$ $\div$10${}^{4}$${}^{ }$, число Прандтля Pr = 0.7, $\textit{g}$ = 1.4, $\textit{w}$ = 0.8. Значения величин на всех рисунках приведены для одного момента времени $\textit{t }$= 1.5, шаг по времени $\textit{t}$ = 0.0002, расчётная область содержит 501$\times$151 узлов.
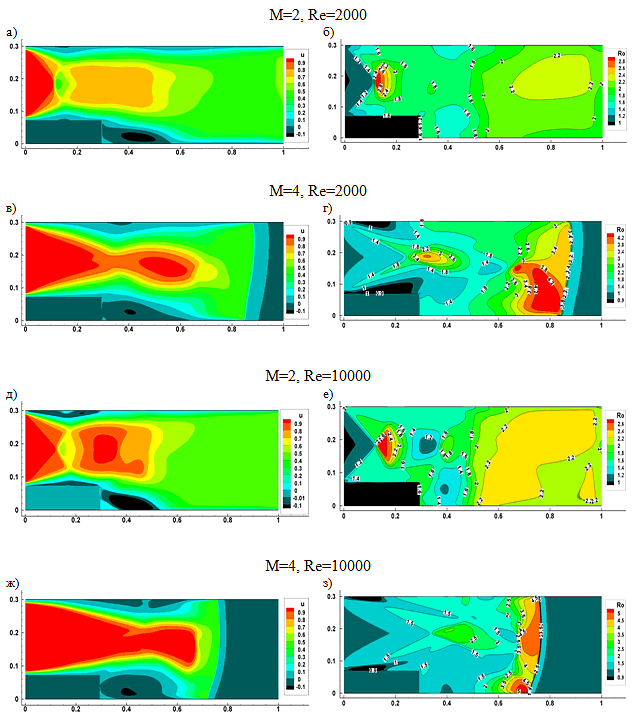
Рис. V.25. Течение за уступом с твёрдой стенкой при различных значениях чисел Маха и Рейнольдса. Поле скоростей (слева) и изолинии плотности (справа)
Как следует из расчётов, для малых чисел Маха за уступом формируется вихрь, о чём свидетельствуют отрицательные значения скорости, для больших чисел Маха за уступом формируется зона с нулевыми значениями скорости. С уменьшением числа Рейнольдса увеличивается вихревая зона и наоборот.
В заключение следует отметить, что полученные системы уравнений удовлетворяют законам сохранения массы и полной энергии на дискретном уровне, обеспечивая устойчивость дискретного решения по времени. Замена искомых функций в уравнениях неразрывности и внутренней энергии обеспечивает повышение точности приближенного решения, и приводит к меньшей абсолютной погрешности в норме $L_{2} $ и $L_{\infty } $. Применение комбинации метода траекторий и метода конечных элементов не требует согласования триангуляций на соседних временных слоях, что значительно облегчает динамическое разрежение или сгущение триангуляций по времени для оптимизации вычислительной работы или улучшения аппроксимации в пограничных слоях и ударных волнах. Для решения систем алгебраических уравнений используется многосеточный метод с внешними итерациями по нелинейности. Совокупность метода траекторий и метода конечных элементов позволяет построить экономичный алгоритм с вычислительной точки зрения.
Блок 3. Создание новых и адаптация известных вычислительных методов повышенного порядка точности для решения уравнений Навье-Стокса вязкого теплопроводного газа (А. В. Вяткин, В. В. Шайдуров).
Уравнения неразрывности, количества движения и энергии переписаны в виде, включающем полную (субстанциональную) производную. Построен итерационный численный метод аппроксимации полной производной, теоретически позволяющий получать численное решение любого порядка точности. Алгоритм применен для решения уравнения переноса, и в указанном случае, основывался на коррекции правой части дифференциального уравнения следующим образом:
\[\begin{array}{l} {L^{h} \rho _{1}^{h} =f^{h} ,} \ {L^{h} \rho _{i}^{h} =f^{h} +L^{h} \rho _{i-1}^{h} -S^{h} \rho _{i-1}^{h} ,{\rm \; \; \; }i=2,...} \end{array}\]
Здесь $L^{h} $ — устойчивый разностный оператор первого порядка точности, $S^{h} $ — специальным образом построенный разностный оператор высокого порядка точности, $\rho _{i}^{h} $ — численное решение, полученное на $\textit{i}$-ой итерации с $\textit{i}$-ым порядком точности. Порядок численного решения $\textit{i}$ не может превышать порядок точности оператора $S^{h} $. Полученные результаты вычислительного эксперимента (рис. V.26) в одномерном случае подтвердили теоретические выкладки о получении численного решения вплоть до четвертого порядка точности. Вместе с тем, при сравнении результатов расчетов с методом экстраполяции Ричардсона (рис. V.27) выяснилось, что последний дает более стабильную, плавную сходимость к численному решению, что при прочих равных обстоятельствах является предпочтительнее.
На рис. V.26 и рис. V.27 по оси абсцисс отмечено число $\textit{n}$ такое, что $N=10\cdot 2^{n} $, где N — число узлов. По оси ординат представлены значения $\log _{2} \frac{\left\| \rho -\rho ^{h,n} \right\| _{\infty } }{\left\| \rho -\rho ^{h,n+1} \right\| _{\infty } } $, характеризующие порядок сходимости.
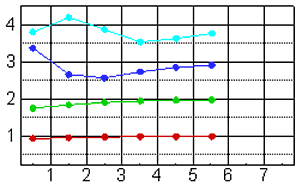
Рис. V.26. Порядок точности решения методом коррекции правой части
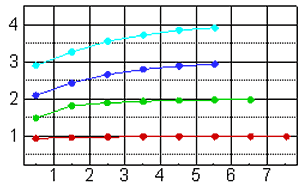
Рис. V.27. Порядок точности решения методом экстраполяции Ричардсона
Блок 4. Организация и проведение летней международной школы (В. В. Шайдуров, Е. Д. Карепова, М. П. Варыгина).
С 4 по 17 июля в Пекинском университете аэронавтики и астронавтики (Beijing University of Aeronautics and Astronautics) прошла международная летняя школа International Summer School «Design of Shape Optimization and Parallel Computing».
На школе с лекциями выступили:
- Prof. Dr.-Ing. Dr. h.c. Dr. h.c. Michael Resch «Simulation and Visualization on Supercomputers in Engineering» (High Performance Computing Center Stuttgart (HLRS) of the University of Stuttgart);
- Prof. Dr. Olivier Pironneau «Mesh Adaption, Optimal Shape Design and Adjoint Equations for Aerospace» (University of Paris VI, Laboratoire J. L. Lions);
- член-корреспондент РАН профессор В. В. Шайдуров «Несколько шагов к необходимой точности расчетов для уравнений Навье-Стокса для вязкого теплопроводного газа» (ИВМ СО РАН).
В рамках проекта были разработаны и прочитаны следующие курсы:
- к.ф.-м.н., доцент Е. Д. Карепова «Ввведение в параллельное программирование»;
- к.ф.-м.н. М. П. Варыгина «Введение в технологию CUDA».
Кроме того, при поддержке Службы редств телекоммуникации и вычислительной техники ИВМ СО РАН (ответственный ст. программист А. В. Малышев) был организован удаленный доступ к малому кластеру ИМ СФУ и вычислительной системе с видеокартой Nvidia Tesla C2050 для проведения практикумов по параллельному программированию:
- к.ф.-м.н., доцент Е. Д. Карепова «Ввведение в MPI»;
- к.ф.-м.н. М. П. Варыгина «Программирование с помощью технологии CUDA».
Основные публикации:
К блоку 1-2:
- Шайдуров В. В., Щепановская Г. И., Якубович М. В.
Применение метода траекторий и метода конечных элементов в моделировании движения вязкого теплопроводного газа // Вычислительные методы и программирование. — 2011. — Т. 12. — С. 275–281 . - Шайдуров В. В., Щепановская Г. И.
О повышении точности приближённого решения уравнений Навье-Стокса для вязкого теплопроводного газа // Междунар. конф. «Современные проблемы прикладной математики и механики: теория, эксперимент и практика [Электронный ресурс]" . — Новосибирск: ИВТ СО РАН. — 2011. — № гос. регистрации — 0321101160, Режим доступа: http://conf.nsc.ru/niknik-90/reportview/39320, свободный. — Загл. с экрана (дата обращения: 15.07.2011). - Шайдуров В. В., Щепановская Г. И., Якубович М. В.
Математическое и численное моделирование течений вязкого теплопроводного газа // Материалы XV Междунар. науч. конф. «Решетневские чтения». — Красноярск. — 2011. — С. 521. - Chen H., Lin Q., Shaidurov V. V., Zhou J.
Error estimates for triangular and tetrahedral finite elements in combination with trajectory approximation of first derivatives for advection-diffusion equations // Numerical Analysis and Applications. — 2011. — V. 4, № 4. — P. 345–362 . - Жоу Юнмин, Лин Кун, Чен Хонгтао, Шайдуров В. В.
Оценки ошибки для треугольных и тетраэдральных конечных элементов в комбинации с траекторной аппроксимацией первых производных для уравнений адвекции-диффузии // Сибирский журнал вычислительной математики. — 2011. — Т. 14. — № 4. — С. 425–442 . - Щепановская Г. И.
The numerical modeling of one-dimensional motion of viscous heat-conductive gas // Материалы XV Междунар. науч. конф. «Решетневские чтения». — Красноярск: СибГАУ. — 2011. — C. 525. - Зализняк В. Е., Щепановская Г. И.
Теория и практика по вычислительной математике. — Красноярск: СФУ. — 2011. — 120 с. - Якубович М. В.
Численное моделирование плоского течения вязкого теплопроводного газа в канале // Программа и тез. докл. XII Всерос. конф. молодых ученых по математическому моделированию и информационным технологиям.? Новосибирск. — 2011. — С. 26.
К блоку 3:
- Вяткин А. В.
Об одной нелинейной разностной схеме 1-го порядка // Тез. XII Всерос. конф. молодых учёных по математическому моделированию и информационным технологиям. — Новосибирск: ИВТ СО РАН. — 2011. — С. 16. - Вяткин А. В.
Нелинейная разностная схема для одного гиперболического уравнения // Материалы XV Междунар. науч. конф. «Решетневские чтения». — Красноярск: СибГАУ. — 2011. — Ч. 2. — С. 539.
(Отделы Вычислительной математики и Вычислительной механики деформируемых сред)
| К началу | |
Проект № 103. «Законы сохранения, инварианты, точные и приближенные решения для уравнений гидродинамического типа и интегральных уравнений»
Координаторы проекта: д.ф.-м.н., проф. С. Б. Медведев, д.ф.-м.н., проф. М. Ю. Филимонов, д.ф.-м.н., проф. К. В. Кошель
Ответственный исполнитель от ИВМ СО РАН: д.ф.-м.н., проф. О. В. Капцов
Исполнитель: Ю. В. Шанько
Изучался специальный класс нелинейных переопределенных систем уравнений в частных производных с двумя независимыми переменными и любым числом искомых функций. Введено новое понятие результанта системы нелинейных уравнений с частными производными. В терминах результантов получен эффективный критерий конечномерности многообразия решений конкретных классов систем уравнений. Получена оценка типа Безу размерности многообразия решений и найдены алгебраические условия, при выполнении которых эта оценка достигается.
Для двумерного уравнения распространения звука в неподвижной неоднородной среде выписаны условия, которым должны удовлетворять обобщенные функционально-инвариантные решения. Предложен подход, позволяющий свести соответствующую переопределенную систему дифференциальных уравнений к системе для функций от двух, а не трех независимых переменных, что значительно упрощает ее анализ на совместность.
Основные публикации:
- Капцов О. В.
Системы уравнений в частных производных с конечномерными многообразиями решений // Программирование. — 2011. — № 2. — С. 71-78. - Шанько Ю. В.
Об обобщенных функционально-инвариантных решениях одного уравнения двумерной акустики // Междунар. конф. «Современные проблемы прикладной математики и механики: теория, эксперимент и практика [Электронный ресурс]". — Новосибирск: ИВТ СО РАН. — 2011. — № гос. регистрации — 0321101160, Режим доступа: http://conf.nsc.ru/files/conferences/niknik-90/fulltext/40235/47425/Shanko.pdf, свободный. — Загл. с экрана (дата обращения: 15.07.2011).
(Отдел вычислительных моделей в гидрофизике)
| К началу | |
Проект № 116. «Моделирование, оптимизация и устойчивость конвективных течений»
Координатор проекта: член-корреспондент РАН В. В. Пухначёв
Блок 1: Исследование устойчивости состояния равновесия и стационарных течений в неклассических моделях конвекции
Ответственный исполнитель от ИВМ СО РАН: д.ф.-м.н., проф. В. К. Андреев
Исполнители: В. Б. Бекежанова, Ю. А. Гапоненко, И. И. Рыжков
1. Найдено стационарное одномерное движение трех вязких теплопроводных жидкостей в плоских слоях, формирующееся одновременно под действием перепада давления и эффектов Марангони на двух поверхностях раздела. На рис. V.28 — V.30 представлены типичные профили скоростей для некоторых значений определяющих параметров: N — безразмерный градиент давления, M1, M2 — числа Марангони.
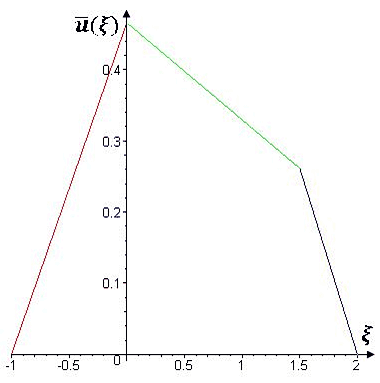
Рис. V.28. Профили скоростей в слоях при N = 0.0001, M1 = 2, M2 = 3
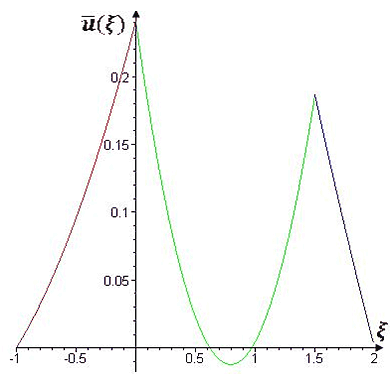
Рис. V.29. Профили скоростей в слоях при N = 0.04, M1 = 2, M2 = 3
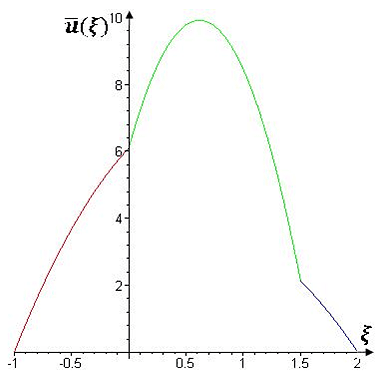
Рис. V.30. Профили скоростей в слоях при N = −10, M1 = 2, M2 = 3
На рис. V.28 изображён случай, когда |N|<<|Mj|, тогда преобладают термокапиллярные силы и имеем почти линейный профиль скоростей — течение Куэтта. На рис. V.29 — случай, когда |N|>>|Mj|, тогда главными становятся градиенты давления в слоях и профили являются параболическими — течение Пуазейля. Рис. V.30 отражает случай примерно одинакового вклада в механизм течения указанных выше факторов. Отметим также, что во втором случае возникает зона возвратного течения в среднем слое — скорость нём меняет знак.
2. Решена задача стационарного сопряженного теплообмена двух контактирующих цилиндров, когда температура задана на всей границе. Распределение температур найдено в виде рядов Фурье, доказана их сходимость и установлена единственность решения. Подобного рода задачи возникают при хранении жидких сред в больших резервуарах, что часто приводит к расслоению этих сред. В результате в сосуде образуется поверхность раздела и система может находиться в равновесии даже при наличии теплообмена между фракциями.
3. Для изучения процессов, происходящих при выращивании кристаллов методом зонной плавки, широко используется модель жидкого моста. Эта модель представляет собой жидкий цилиндр, помещенный между двумя стержнями с различной температурой. Наличие градиента температуры на свободной границе приводит к возникновению термокапиллярного течения, которое направлено от нагретого стержня к холодному и является стационарным при небольших разностях температур. При достижении критической разности температур стационарное движение становится неустойчивым. Наличие подобных неустойчивостей в зоне расплава может существенно повлиять на качество кристалла.
Одним из методов управления устойчивостью стационарного движения является обдувание жидкого моста потоком газа. Взаимодействие механических напряжений на границе раздела может влиять на устойчивость системы в зависимости от направления прокачки газа и термокапиллярного течения жидкости на границе раздела.
В рамках данного проекта было проведено исследование термокапиллярных течений в двухфазной системе, состоящей из бесконечного жидкого цилиндра, обдуваемого потоком газом. Слой газа ограничен внешней твердой стенкой, которая может двигаться в вертикальном направлении. Найдено точное решение, описывающее стационарное движение, исследованы возможные режимы течений и их устойчивость в линейном приближении.
На рис. V.31 показаны профили скорости в жидкой и газовой фазе для различных значений безразмерного расхода газа $\textit{Q}$ через поперечное сечение цилиндрического слоя в системе силиконовое масло (2 сСт) — воздух.
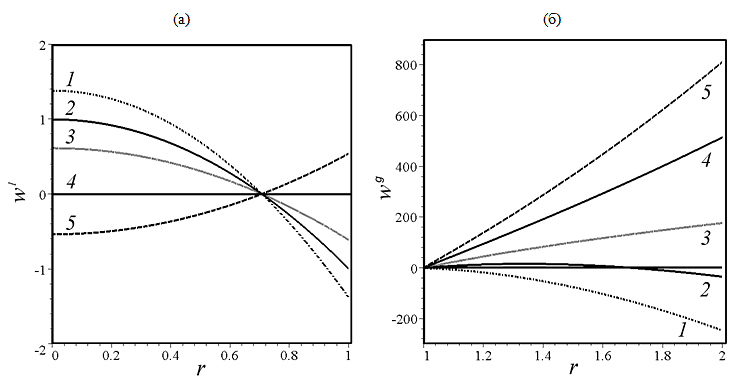
Рис. V.31. Профили скорости в жидкой (а) и газовой фазе (б) для различных значений безразмерного расхода газа $\textit{Q}$: 1: $\textit{Q }=-1$; 2: $\textit{Q }$= 0; 3: $\textit{Q }$= 1; 4: $\textit{Q }$= 2.6; 5: $\textit{Q }$= 4. Система силиконовое масло (2 сСт) — воздух. Число Марангони Ma = 150. Отношение радиусов слоя газа и жидкого цилиндра $\gamma $ = 2
Карта устойчивости двухфазных течений представлена на рис. V.32 в пространстве параметров расход газа $\textit{Q}$ — число Марангони Ma для недеформируемой границы раздела. Если направление прокачки газа совпадает с направлением термокапиллярного течения на границе раздела (расход газа $\textit{Q }$$<$ 0), то граница устойчивости (критическое число Марангони Мa) понижается по сравнению со случаем $\textit{Q }$= 0. При изменении направления прокачки на противоположное ($\textit{Q}$ $>$ 0), граница устойчивости системы сначала слегка повышается, а затем вновь понижается. Увеличение расхода $\textit{Q}$ при фиксированном значении числа Марангони приводит к подавлению термокапиллярного течения в жидкости потоком газа (режим 4 на рис. V.31, жирная линия на рис. V.32). При дальнейшем увеличении $\textit{Q}$ направление термокапиллярного движения на границе раздела меняется. Данный режим является устойчивым при небольших числах Марангони и расходах газа.
4. Дано прямое численное решение осесимметрической задачи взаимодействия жидкого моста с коаксиальным потоком газа. Расчеты проводились для силиконового масла и воздуха с параметрами, приведенными в табл. V.3.
Основными параметрами являются длина жидкой зоны $\textit{d}$, ее радиус $\textit{R}$${}_{0}$, внешний радиус $\textit{R}$${}_{1}$, числа Марангони Ma, Прандтля Pr, Рейнольдса Re и аспектное число $\Gamma ={d\mathord{\left/ {\vphantom {d R_{0} }} \right.} R_{0} } .$ Для расчетной конфигурации $\Pr ^{l} =68;$ $\Pr ^{g} =0,75;$ $Re^{g} =280U_{0}^{g} ;$ ${\rm Ma}=1,91\cdot 10^{5} \Delta Td,$ где индекс $\textit{l }$относится к силиконовому маслу, а $\textit{g }$ — к газу; $U_{0}^{g} $ — скорость газа на входе, $\Delta T$ — разность температур на твердых стержнях.
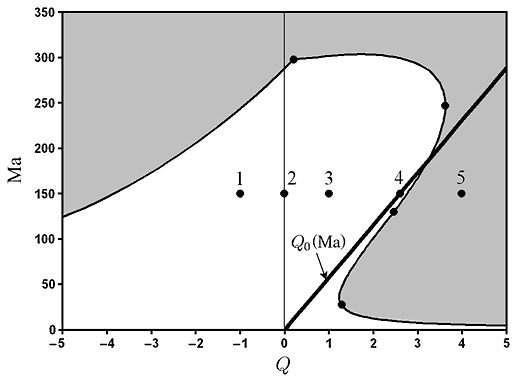
Рис. V.32. Карта устойчивости в прост-ранстве параметров расход газа Q — число Марангони Ma. Система неустойчива в заштрихованной области. Критическое азимутальное волновое число m = 1. Точками обозначены пары значений (Q, Ma), соответствующие графикам 1-5 на рис. V.31
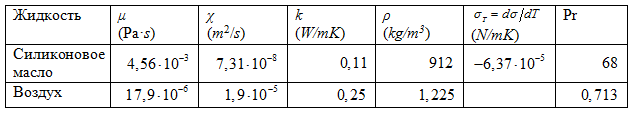
Таблица V.3. Характеристики жидкости
На рис. V.33 дана стационарная структура течения для пассивного газа («кошачьи глаза»). Течение возникает только под давлением термокапиллярных сил.
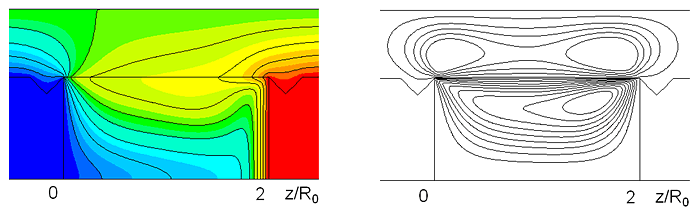
Рис. V.33. Поля температур и изолинии функций тока в случае пассивного газа при $\Delta T=5K,$ $U_{0}^{g} =0,$ $T_{g}^{} =T_{0}, $ $\Gamma =2$
Картина развития осцилляционной неустойчивости представлена на рис. V.34 — V.35. Она возникает за счет взаимодействия термокапиллярного движения (от горячей стенки к холодной) и движения газа, направленного в противоположную сторону.
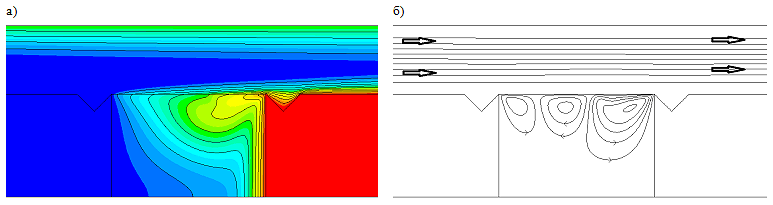
Рис. V.34. Моментальный снимок полей (а) температур, (б) течений при $\Delta T=20K,$ $U_{0}^{g} =3\, {m\mathord{\left/ {\vphantom {m s}} \right.} s}, $ $\Gamma =1,5$
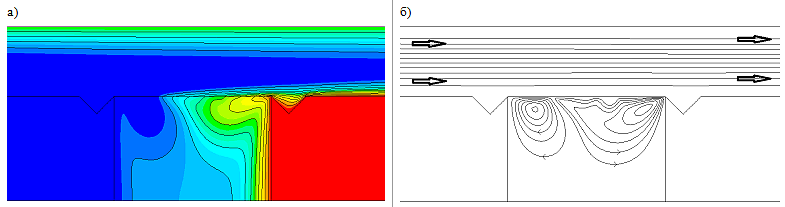
Рис. V.35. Моментальный снимок полей (а) температур, (б) течений при $\Delta T=20K,$ $U_{0}^{g} =4\, {m\mathord{\left/ {\vphantom {m s}} \right.} s}, $ $\Gamma =1,5$
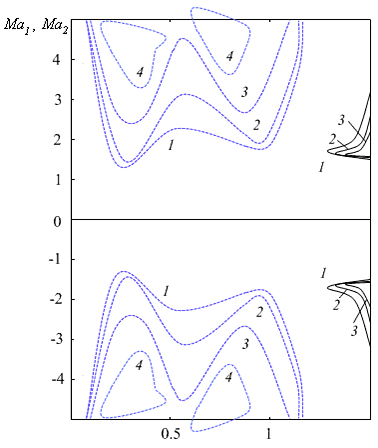
Рис. V.36. Нейтральная тепловая мода: 1−3 — $h=10^{4}, \, 10^{2}, \, 1,$ $M_{1} =M\cdot 10^{3} ;$ 4 — $h=10^{4}, \, $ $M_{2} =M\cdot 10^{4} $
5. Изучена задача о плоском однонаправленном двухслойном течении вязкой теплопроводной жидкости при совместном действии градиента давления и сил Марангони в условиях невесомости. Плоский слой ограничен твердыми стенками, одна из которых может двигаться. На внешних границах поддерживаются линейные распределения температур. Данная задача допускает решение типа Остроумова — Бириха. Меняя скорость движения стенки, градиенты давления и температуры, можно получать различные режимы течений. Если во втором слое потребовать выполнения условия замкнутости потока, то, задавая скорость движения стенки специальным образом, можно получить такой режим, что второй слой будет оставаться в покое, а в первом реализуется течение Куэтта. Такое течение формируется только под действием термокапиллярных сил и движения твердой стенки.
Методом линеаризации исследована устойчивость указанного течения. Найдено асимптотическое поведение комплексного декремента в длинноволновой области для недеформируемой поверхности раздела. Получены аналитические представления собственных функций в случае плоских возмущений. Показано, что кризис вызывается тепловой модой (рис. V.36), при этом неустойчивость может иметь как колебательный (следствие несамосопряженности спектральной задачи), так и монотонный характер. Тип наиболее опасных возмущений зависит от длины волны возмущений. Определена общая асимптота монотонной неустойчивости для любых значений толщин слоев $M=\pm 1494.26$, здесь $\textit{М }$ — число Марангони, отрицательные значения соответствуют скорости движения стенки, противоположной направлению течения Куэтта в первом слое.
Основные публикации:
- Andreev V. K.
Properties of the Solution of the Adjoint Problem Describing the Motion of Viscous Fluids in a Tube // Differential Equations. — 2011. — Т. 47, № 5. -P. 671–680 . - Бекежанова В. Б.
Конвективная неустойчивость течения Марангони-Пуазейля при наличии продольного градиента температуры // ПМТФ. — 2011. — Т. 52. — № 1. — С.92–100 . - Бекежанова В. Б. Андреев В. К.
Об однонаправленном двухслойном течении в условиях микрогравитации // Вестник Нижегородского ун-та им. Н. И. Лобачевского. — 2001. — № 4(3). — С. 639–640 . - Магденко Е. П.
Решение стационарной сопряженной задачи теплообмена в конечных цилиндрах // J. of Siberian Federal University. Mathematics and Physics. — 2011. — № 4(4). — P. 519–526 . - Рыжков И. И.
Об устойчивости плоского слоя многокомпонентной смеси с эффектом Соре // Вестник Нижегородского ун-та им. Н. И. Лобачевского. — 2011. — № 4(3). — С. 1080–108 1. - Ryzhkov I. I.
Thermocapillary instabilities in liquid bridges revisited // Physics of Fluids. — 2011. — V. 23 (8). — P. 82103. — doi: 10.1063/1.3627150. - Gaponenko Yu., Nepomnyashchy A. and Shevtsova V.
Thermocapillary and shear driven flows in gas/liquid system in annular duct // J. of Physics: Conference Series. (In press). - Лемешкова Е. Н.
Стационарное течение трех жидкостей в плоском слое под действием термокапиллярных сил и перепада давления // J. of Siberian Federal University. — Mathematics and Physics. (В печати).
(Отдел дифференциальных уравнений механики)
| К началу | |