| ИВМ СО РАН | Поиск |
| Отчеты ИВМ СО РАН |
Отчет ИВМ СО РАН за 2008 год
Программы фундаментальных исследований Сибирского отделения РАН
Механика, энергетика
Направление 3.5 «Общая механика, динамика космических тел, транспортных средств и управляемых аппаратов; биомеханика; механика жидкости, газа и плазмы, неидеальных и многофазных сред; механика горения, детонации и взрыва»
Программа 3.5.1 «Построение и анализ новых математических моделей движения сложных сред»
Координатор программы: ак. РАН Л. В. Овсянников
Проект № 3.5.1.3 «Математическое и компьютерное моделирование движения сложных сред с поверхностями раздела»№ гос. регистрации 01.2.007 09438
Научный руководитель проекта: д.ф.-м.н., проф. В. К. Андреев
Блок 1: Исследование устойчивости равновесных состояний и движений плоских слоёв с поверхностями раздела в неклассических моделях конвекции.
1.1. Методами численного моделирования для системы уравнений конвекции, полученной осреднением, исследована задача о смешивании бинарной смеси в прямоугольной области при условиях пониженной гравитации в быстроменяющемся внешнем горизонтальном силовом поле. Начальное состояние системы имеет узкую поверхность раздела двух компонентов смеси, что соответствует условию устойчивого равновесия. Задача рассматривалась применительно к водно-спиртовым растворам с учетом зависимости коэффициентов вязкости и диффузии от концентрации.
В случае отсутствия гравитации после начала вибрации потоки компонентов смеси проникают друг в друга в режиме пристеночного течения. При этом неоднородное распределение вертикальной скорости в потоке приводит к образованию неустойчивости Кельвина-Гельмгольца. На более позднем этапе развитие течения приводит к ситуации, когда один компонент проникает в другой внутри слоя с образованием структуры, характерной для неустойчивости Рэлея-Тейлора. При параметрическом исследовании динамики системы обнаружено, что структура течения существенно зависит от вертикальной составляющей внешнего постоянного силового поля (гравитации).
В зависимости от параметров задачи обнаружены различные режимы течения. Так, при доминировании вибрационной нагрузки над гравитационной (Gs/Ra > 3) наблюдается интенсивный пристенный режим смешивания компонентов с образованием структур течения, характерных для неустойчивости Кельвина-Гельмгольца. Уменьшение интенсивности вибрации приводит к сокращению заброса массы вдоль вертикальных стенок и, в предельном случае, к диффузионному режиму смешивания компонентов. Для рассмотренной конфигурации построена диаграмма устойчивости, которая определяет переход от одного режима течения к другому.
При исследовании смешивания слоев различной толщины обнаружены режимы вибрации, при которых происходит растворение только одного из компонентов с сохранением неизменной формы переходной поверхности раздела. В случае смещенной от центра переходной зоны происходит диссипация только одного из компонентов раствора.
1.2. Проведено исследование устойчивости конвективного течения многокомпонентной смеси в термогравитационной колонне, когда жидкость находится в вертикальном слое, подогреваемом сбоку. Термодиффузионное разделение смеси между боковыми стенками вместе с вертикальным конвективным потоком приводит к разделению компонентов в вертикальном направлении. Измерение этого разделения в стационарном состоянии позволяет определить коэффициенты термодиффузии. При увеличении разности температур основное конвективное течение может стать неустойчивым.
В рамках линейной теории проведены расчеты критических параметров неустойчивости методом Галеркина, а также методом пошагового интегрирования с ортогонализацией. Впервые исследована устойчивость тройных смесей в колонне. Кроме этого, проведены расчеты для бинарных смесей в широкой области параметров. Полученные результаты показывают, что термогравитационная колонна может использоваться для измерения коэффициентов диффузии и термодиффузии в тройных смесях, в которых один из компонентов имеет отрицательных эффект Соре. Также установлено, что уменьшение поперечной длины колонны оказывает стабилизирующий эффект на поперечные возмущения. Результаты данного исследования имеют важное значение для разработки экспериментальных установок и планирования измерений в многокомпонентных системах.
1.3. Исследована устойчивость равновесного состояния бинарных смесей с общей поверхностью раздела и одной свободной границей. Нижняя граница системы — неподвижная твердая стенка, верхняя — недеформируемая свободная поверхность.
С помощью уравнений малых возмущений исследуется устойчивость равновесного состояния. Определяющими параметрами полученной задачи являются числа Марангони, Соре, Вебера, Био; кроме того, считается, что поверхностное натяжение на поверхности раздела и свободной границе линейно зависит от температуры и концентрации.
Построены нейтральные кривые для различных значений числа Соре Sr на поверхности раздела, характеризующего действие эффекта термодиффузии. Оказалось, что с усилением термодиффузионного эффекта (рост числа Соре) увеличивается область длинноволновой устойчивости.
Исследовано влияние числа Вебера We на устойчивость термодиффузионного равновесия.
Расчеты показали, что с ростом числа Вебера критические значения числа Марангони уменьшаются, при этом область длинноволновой устойчивости увеличивается.
1.4. Изучена задача об устойчивости двухслойного течения вязкой термокапиллярной жидкости. Гладкая поверхность Γ делит область течения на две подобласти Ω2 = {|x| < ∞, −h2 < y < 0} и Ω1 = {|x| < ∞, 0 < y < h1}. Предполагается, что Ω2 занята более тяжелой жидкостью. При этом считается, что система произвольно ориентирована относительно силы тяжести. В каждой из областей справедлива система уравнений Обербека-Буссинеска.
Поверхность раздела жидкостей Γ фиксирована и на ней заданы кинематическое, динамическое и энергетическое условия. Предполагается, что коэффициент поверхностного натяжения линейно зависит от температуры. На твердых стенках заданы условия прилипания и линейный закон изменения температуры на стенках.
Выписаны уравнения малых возмущений стационарных течений жидкости. На их основе исследована устойчивость течения двух несмешивающихся несжимаемых теплопроводных вязких жидкостей при совместном действии массовых и термокапиллярных сил.
Проведено сравнение с решением аналогичной задачи при отсутствии массовых сил. На основе численных расчетов показано стабилизирующее влияние гравитационных сил.
1.5. Изучено инвариантное решение уравнений термодиффузионного движения вида wj = wj(r,t), pj = −ρjfj(t)z + Pj(t), θj = Az + Tj(r,t), c = Bz + K(t), j = 1,2. Оно описывает однонаправленное нестационарное движение бинарной смеси в трубе радиуса b. Смесь занимает область 0 ≤ r ≤ a < b, а вязкая теплопроводная жидкость — цилиндрический слой a ≤ r ≤ b, так что wj(r,t) — осевая скорость смеси и жидкости, pj,θj — распределение давления и температуры в них, а c(z,r,t) — концентрации в смеси. Первоначально смесь и жидкость находятся в покое, затем при t > 0 градиенты давлений fj(t) порождают их движение, причём цилиндрическая поверхность r = a во все моменты времени остаётся их поверхностью раздела. Функции wj(r,t), Tj(r,t), K(r,t) можно назвать возмущениями состояния покоя.
Блок 2: Построение на основе метода симметрий точных решений уравнений: движения смесей с учётом эффектов Соре и Дюфура, стационарных моделей турбулентности.
2.1. Для системы уравнений термодиффузионного течения с учетом сил плавучести, нелинейно зависящих от температуры, давления и концентрации, построено 7 инвариантных подмоделей, которые проинтегрированы в квадратурах, тем самым получены новые точные решения уравнений модели. В случае, когда функция, отвечающая за силу плавучести, зависит от температуры и концентрации, для двух полученных инвариантных решения уравнений модели поставлены граничные условия на твердых стенках или на свободной границе. При данных граничных условиях решение описывает обобщение течения Пуазейля, возникающего в горизонтальном слое под действием постоянного градиента давления при линейно распределенных температуре и концентрации в зависимости от поперечной координаты. Профиль скоростей, как и в течении Пуазейля, параболический.
Решение другой краевой задачи при условиях, заданных на твердой стенке и свободной границе, описывает состояние покоя жидкости при линейно распределенных температуре и концентрации в зависимости от поперечной координаты.
2.2. Для уравнений вращательно-симметричного движения идеальной жидкости в лагранжевых координатах
на основе групповой классификации уравнений относительно функции V(η,ζ) = η2ν02(η,ζ) построены новые точные решения. Например, для функции V = αζ + F(η), α = const на операторе <2(δη + δζ) − αr−2δp> точным является решение вида
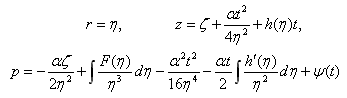
с произвольными функциями F(η), h(η), Ψ(t). Возможна следующая интерпретация решения: цилиндрические поверхности во все моменты времени состоят из одних и тех же частиц. Движение происходит по спиралям вдоль направления z с азимутальной скоростью
Цилиндрические поверхности также можно считать твердыми стенками.
Блок 3: Исследование групповых свойств расширенной k-e модели турбулентности в приближении дальнего турбулентного следа.
Выполнен теоретико-групповой анализ математических моделей второго порядка дальнего плоского турбулентного следа за цилиндром в пассивно стратифицированной среде и следе за нагретым цилиндром. Найдены первые интегралы систем обыкновенных дифференциальных уравнений, полученных в результате редукций исходных моделей относительно подгрупп растяжений. Построены автомодельные решения, удовлетворительно согласующиеся с экспериментальными данными.
Блок 4: Численное исследование биологических и гидрофизических механизмов формирования неоднородных распределений компонент озерных экосистем. Выполнение вычислительных экспериментов по исследованию биологических и гидрофизических механизмов формирования пространственно неоднородных распределений компонент озерных экосистем.
Выполнена стыковка численных расчетов гидрофизических процессов с блоком расчетов гидробиологических и гидрохимических характеристик. Проведены исследования динамики вертикальной структуры стратифицированного водоема (на примере озера Шира). Показано, что чем больше толщина льда, тем больше толщина слоя перемешивания; чем преснее вода, тем толще слой льда. Толщина слоя конвективного перемешивания зависит не только от метеоданных в зимний период, но и от метеоданных в осенний период. При увеличении температуры и солености воды в поверхностном слое и уменьшении толщины этого слоя в предледоставный период толщина слоя конвективного перемешивания увеличивается. Вертикальные распределения температуры и солености воды определяют вертикальные распределения гидробиологических характеристик.
Разработан комплекс программ для исследования гидрофизических и гидробиологических процессов в озере Шира. Гидрофизические параметры служит входными данными для биологических процессов. Биологические компоненты описываются уравнениями конвекции-диффузии. Для озера Шира в данный момент моделируется около 30 компонент. Программы позволяют проводить расчёты, изменяя начальные данные, метеоданные, параметры, сетку. Выполнены пробные расчеты.
Блок 5: Построение двумерной численной модели для течений с капиллярными менисками.
На основе метода частиц для несжимаемой жидкости построена двумерная численная модель для исследования известной проблемы о форме мениска и динамическом контактном угле в окрестности движущейся контактной линии. Рассматривается плоская задача о погружении пластины в жидкость. Основное противоречие, заключающееся в несовместности условия прилипания в точке контакта с кинематикой и динамикой задачи, обходится экстраполяцией формы свободной границы с помощью сплайна, имеющего заданный (статический) угол контакта на движущейся стенке. Это приводит, к некоторой процедуре проскальзывания точки контакта. В методе используется подвижная неравномерная сетка, сгущающаяся в окрестности точки контакта и отслеживающая ее положение. Результаты расчетов показывают правильное качественное предсказание моделью зависимости динамического контактного угла от капиллярного числа и неплохое количественное совпадение с экспериментальными данными.
Основные публикации.
К блоку 1:
- Андреев В. К., Собачкина Н. Л.
Движение бинарной смеси в горизонтальной цилиндрической трубе // Вычислительные технологии. — 2008. — Т. 13. — № 2. — С. 3-14. - Gaponenko Yu., Shevtsova V. M.
Mixing Under Vibrations in Reduced Gravity // Microgravity Science and Technology, Springer. — 2008. — Vol. 20. — № 3-4. — P. 307–311 . - Mialdun A., Ryzhkov I. I., Melnikov D. E., and Shevtsova V.
Experimental evidence of thermal vibrational convection in non-uniformly heated fluid in a reduced gravity environment // Physical Review Letters. — 2008. — Vol. 101, 084501. - Melnikov D. E., Ryzhkov I. I., Mialdun A., Shevtsova V.
Thermovibrational convection in microgravity: preparation of a parabolic flight experiment // Microgravity Science and Technology. — 2008. — Vol. 20. — P. 29-39.
К блоку 2:
- Родионов А. А., Степанова И. В.
Групповая классификация уравнений модели конвекции с учетом сил плавучести // Вычислительные технологии. — 2008. — Т. 13. — № 5. — С. 61-69. - Степанова И. В.
О некоторых точных решениях модели конвекции с учетом сил плавучести // Материалы конф. молодых ученых ИВМ СО РАН. — Красноярск: ИВМ СО РАН. — 2008. — С. 10-17.
К блоку 3:
- Капцов О. В., Ефремов И. А., Шмидт А. В.
Автомодельные решения модели второго порядка дальнего турбулентного следа // ПМТФ — 2008. — Т. 49. — № 2. -С.74-78. - Капцов О. В., Ефремов И. А., Шмидт А. В.
Автомодельные решения одной модели дальнего турбулентного следа // Тез. докл. междунар. конф. «Дифференциальные уравнения. Функциональные пространства. Теория приближений». — Новосибирск. — 2008. — С. 497.
К блоку 4:
- Белолипецкий В. М., Генова С. Н.
Численное моделирование годовой динамики вертикальной структуры соленого озера // Вычислительные технологии. — 2008. — Т. 9. — № 4. — С. 34-43. - Белолипецкий В. М., Генова С. Н.
Численные расчеты вертикальных распределений температуры и солености воды в озере Шира // Вычислительные технологии. — 2008. — Т. 13. — Вестник КазНУ им. Аль-Фараби, сер. Математика, механика, информатика. — № 3(58). — Ч. 1. — С. 261–266 . (Совместный выпуск).
(Отделы вычислительных моделей в гидрофизике, дифференциальных уравнений механики)
| К началу | |
Направление 3.6 «Механика твердого тела, физика и механика деформирования и разрушения, механика композиционных и наноматериалов, трибология»
Программа 3.6.3 «Механика деформирования и разрушения однородных и композитных материалов и конструкций для транспортных и авиационных систем»
Координатор программы: чл.-корр. РАН Б. Д. Аннин
Проект № 3.6.3.3 «Разработка вероятностных моделей предельных состояний, ресурса и живучести материалов и конструкций технических систем для оценки показателей техногенного риска»№ гос. регистрации 01.2.007 09436
Научный руководитель проекта: д.т.н., проф. В. В. Москвичев
Разработка моделей предельных состояний элементов конструкций и структурно-неоднородных материалов на базе критериев линейной и нелинейной механики разрушения для случаев многоочаговых повреждений технологического и эксплуатационного происхождения.
Разработана база данных «Статистика дефектности и расчетных характеристик», включающая информацию по технологической дефектности сварных конструкций, эксплуатационной дефектности технических систем различного назначения, характеристикам механических свойств и трещиностойкости конструкционных сталей. Данная информация является основой для модельных расчетов показателей техногенного риска оборудования и конструкций опасных производственных объектов.
Проведен анализ живучести технических систем и оборудования. Технологическое оборудование ранжируется по степени опасности. Анализ схем взаимодействия элементов производственных систем позволяет отнести любую единицу оборудования к одной из двух технологических групп.
К I группе отнесены те единицы оборудования, полные или частичные отказы которых таким образом влияют на технологические процессы, потоки материалов и энергии, что создаются дополнительные нагрузки (механические, термические, электромагнитные и др.) на другие единицы оборудования. Ко II группе относятся единицы оборудования, отказы которых не влияют на нагруженность и надежность смежных единиц оборудования посредством изменения протекания технологических процессов. Оборудование, относящееся к I технологической группе, дополнительно делится на три подгруппы: I/I — оборудование, отказы которого создают дополнительные нагрузки, не оказывающие значительного влияния на работоспособность и ресурс смежных единиц оборудования, ими можно пренебречь; I/II — оборудование, отказы которого создают дополнительные нагрузки, приводящие к ограничению работоспособности и (или) снижению ресурса смежных единиц оборудования; I/III — оборудование, отказы которого создают дополнительные нагрузки, приводящие к повреждениям и отказам смежных единиц оборудования. Таким образом, устанавливается взаимосвязь между напряженно-деформированным состоянием (НДС), отказами и разрушениями смежных в производственной системе единиц оборудования.
К 1 группе опасности относится оборудование, отказы которого непосредственно приводит к человеческим жертвам и убыткам, сопоставимым с оборотными средствами предприятия.
Во 2 группу опасности включено оборудование, отказы которого непосредственно приводит к убыткам, сопоставимым со стоимостью всего оборудования цеха (отделения) или может привести к нарушению в работе более крупного или опасного оборудования.
В 3 группу опасности входит оборудование, отказы которого не приносит больших убытков непосредственно, но может нанести вред производству, если не будет своевременно устранено.
Таким образом, выделены те типы оборудования, для которых вопросы оценки и обеспечения живучести являются наиболее актуальными (III подгруппа I технологической группы). Для этих типов оборудования в зависимости от группы их опасности требуются различные подходы и различный уровень регламентации требований к живучести (группы живучести А, Б, В). По мере снижения уровня требований к обеспечению живучести требуемые технико-технологические параметры могут быть достигнуты и без использования понятия живучести. Напротив, по мере роста этих требований должно возрастать как число расчетных параметров, так и сложность методов и алгоритмов их оценки.
Обоснованы требования для оборудования, относящегося к той или иной группе живучести, основными из которых являются:
Оборудование группы А. При наличии трещиноподобного повреждения длиной l* при циклическом нагружении скорость роста трещины должна быть не более v*, так чтобы
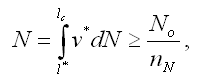
где lc — критический размер трещины; nN — коэффициент запаса по циклической долговечности; Nо — планируемый остаточный срок службы.
Оборудование группы Б. Нормирование эксплуатационной дефектности выполняется по критериям статической прочности с учетом возможных предельных состояний. При наличии трещиноподобного дефекта допустимый его размер должен быть меньше критического. При наличии трещиноподобного дефекта в условиях характерного для металлургического оборудования термомеханического нагружения допустимый размер дефекта должен быть меньше критического, определяемого уровнями действующих напряжений и температур. Прогнозирование остаточного ресурса выполняется с позиций классических представлений об усталостной прочности и с учетом подходов механики разрушения. Остаточный ресурс оценивается для варьируемых размеров дефекта и температурных условий, что требует предварительного обследования зависимостей характеристик напряженного состояния и параметров механики разрушения от размеров дефекта и температурных условий.
Оборудование группы В. Расчетно-экспериментальное обоснование безопасного уровня дефектности в связи с проектным или остаточным сроком службы. Реализация этого требования предполагает проведение численных исследований напряженно-деформированного состояния (НДС), анализа опасности дефектов, расчетной оценки остаточного ресурса и нормирования безопасного уровня дефектности.
4. Модельные расчеты волокнистых композитов с многоочаговыми повреждениями.
Выполнен детальный трехмерный конечно-элементный анализ напряженно-деформированного состояния волокнистого композита при наличии нескольких взаимодействующих микроповреждений структуры: разрыв волокна и отслоение волокна от матрицы. Анализ выполнялся для двух случаев: идеальная связь на поверхности раздела и «скольжение» волокна с учетом трения на контактирующих поверхностях. Влияние на НДС параметров структуры и повреждений, таких как объемное содержание компонентов и длина трещины отслоения, определялось путем сравнения уровня и протяженности зоны возмущения осевых напряжений.
Особенность перераспределения нагрузки в отличие от случая одиночного разрыва волокна заключается в существовании (за исключением малых размеров отслоений) двух максимумов концентрации напряжений в ближайших соседних волокнах — в плоскости обрыва и в области, примыкающей к вершине трещины отслоения. Для относительно больших отслоений концентрация напряжений снижается с возрастанием длины. Эта зависимость является нелинейной — при относительно больших размерах отслоения коэффициент концентрации Kt асимптотически стремится к постоянному значению. Однако несмотря на снижение максимального значения концентрации напряжений при наличии отслоения, возрастает длина зоны перераспределения нагрузки — напряжения, превышающие номинальные (Kt > 1), действуют на большой длине соседних волокон.
Другой особенностью НДС является тот факт, что при малых размерах отслоения (порядка диаметра волокна) максимальный Kt на близлежащем волокне превышает это значение для случая обрыва без отслоения. Это можно объяснить наложением полей напряжений, возникающих в вершинах поперечной и продольной трещин. Отметим, что такая особенность перераспределения напряжений не учитывается ни в одной из известных микромеханических моделей разрушения волокнистых композитов.
В развитии структурно-имитационного подхода разработана вероятностная кинетическая модель разрушения волокнистого композита, полученного методом экструзии алюминиевых сплавов и нанопорошков тугоплавких соединений. Данный материал в отличие от традиционных волокнитов не содержит матрицу, а совместная работа отдельных волокон реализуется за счет их взаимодействия по боковым поверхностям. Исходя из этой особенности, модель структуры материала представляется конечными элементами волокна и элементами, моделирующие сдвиг волокон относительно друг друга. В отличие от большинства существующих структурных моделей, перераспределение напряжений после разрушения волокон учитывается непосредственно при решении системы уравнений МКЭ, а не задается априори.
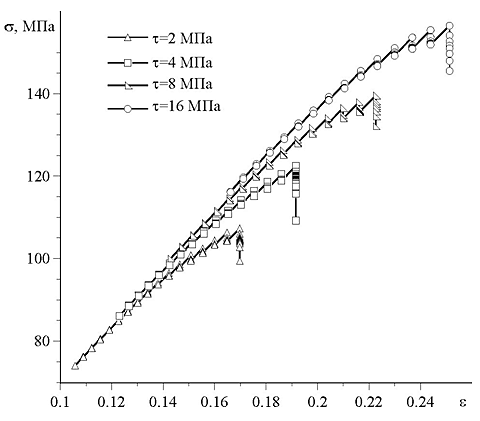
Рис. 16. Расчетные диаграммы деформирования волокнистого композита
На рис. 16 представлены расчетные диаграммы деформирования композита для различных значений τ-параметра, определяющего степень взаимодействия на границе раздела волокон. Последние точки на кривых соответствуют деформации, при которых происходит спонтанное увеличение числа разрушенных элементов. На диаграммах хорошо видны ступенчатое изменение напряжений при одном уровне деформаций, что отражают повышенное сопротивление волокнистых материалов разрушению при наличии поврежденных элементов структуры. При разрушении волокна нагрузка перераспределяется на более прочные объемы материала, устанавливается равновесие и композит вновь может воспринимать повышение нагрузки. Магистральная трещина (или кластеры обрывов волокон) не формируется и не наблюдается асимптотическое снижение предельных напряжений с ростом уровня поврежденности структуры, характерное для однородных материалов. Полученные значения предельных номинальных напряжений хорошо согласуются с экспериментальными данными (122 МПа) при значениях τ = 3,...,6 МПа, что соответствует экспертной оценке этого параметра.
Расчеты по предложенной модели позволили определить основной механизм деформирования и разрушения волокнистого алюминиевого композита, показали возможность ее использования для совершенствования технологии изготовления данного класса материалов.
Основные публикации:
- Кокшаров И. И., Буров А. Е.
Вероятностный анализ разрушения резервированных технических систем с учетом фактора перегрузки // Заводская лаборатория. Диагностика материалов. — 2008. — № 3. — С. 54-57. - Лепихин А. М., Москвичев Е. В.
Вероятностное моделирование предельных состояний и оценка ресурса и надежности трубопроводов // Вычислительные технологии. — 2008. — Т. 13. — С. 47-51. - Буров А. Е.
Анализ стабильности формы элемента из волокнистого композита // Материалы XII Междунар. науч. конф. «Решетневские чтения». — Красноярск: СибГАУ. — 2008. — С. 192–194 . - Махутов Н. А., Гаденин М. М., Москвичев В. В.
Междисциплинарные исследования конструкционной прочности и техногенной безопасности // Машиностроение и инженерное образование. — 2008. — С. 2-11. - Доронин С. В.
Расчеты живучести при проектировании машиностроительных конструкций // Тяжелое машиностроение. — 2008. — № 7. — С. 9-12. - Доронин С. В.
Расчетное обоснование периодичности дефектоскопического контроля и усилений несущих конструкций // Ремонт, восстановление, модернизация. — 2008. — № 8. — С. 7-11. - Доронин С. В.
Обоснование требований к живучести технологического оборудования // Безопасность жизнедеятельности. — 2008. — № 9. — С. 30-33. - Москвичев В. В.
Живучесть элементов конструкций авиационной и космической техники // Материалы XII Междунар. науч. конф. «Решетневские чтения». — Красноярск: СибГАУ. — 2008. — С. 23-24.
(Отдел машиноведения)
| К началу | |