| ИВМ СО РАН | Поиск |
| Отчеты ИВМ СО РАН |
Отчет ИВМ СО РАН за 2008 год
Интеграционные, экспедиционные проекты, гранты СО РАН
- Заказные интеграционные проекты
- Междисциплинарные интеграционные проекты
- Комплексные интеграционные проекты
- Экспедиционные проекты
- Целевая программа СО РАН «СуперЭВМ»
- Целевая программа СО РАН «Информационные и телекоммуникационные ресурсы СО РАН»
Комплексные интеграционные проекты
Проект № 2.15 " Построение и анализ новых математических моделей сложных сред"
Организации-исполнители: ИГиЛ СО РАН, ИМ СО РАН, ИВМ СО РАН
Координаторы: ак. РАН Л. В. Овсянников, ак. РАН С. К. Годунов
Исполнитель от ИВМ СО РАН: д.ф.-м.н., проф. В. К. Андреев
1. Методами численного моделирования для системы уравнений конвекции, полученной осреднением, исследована задача о смешивании бинарной смеси в прямоугольной области при пониженной гравитации в быстроменяющемся внешнем горизонтальном силовом поле. Начальное состояние системы имеет узкую поверхность раздела двух компонентов смеси, что соответствует условию устойчивого равновесия. Задача рассматривалась применительно к водно-спиртовым растворам с учетом зависимости коэффициентов вязкости и диффузии от концентрации.
На рис. 30 представлены результаты (поле концентрации), отражающие динамику распространения примеси в случае отсутствия гравитации. Видно, что после начала вибрации потоки компонентов смеси проникают друг в друга в режиме пристеночного течения. При этом неоднородное распределение вертикальной скорости в потоке приводит к образованию неустойчивости Кельвина-Гельмгольца. На более позднем этапе развитие течения приводит к ситуации, когда один компонент проникает в другой внутри слоя с образованием структуры, характерной для неустойчивости Рэлея-Тейлора.
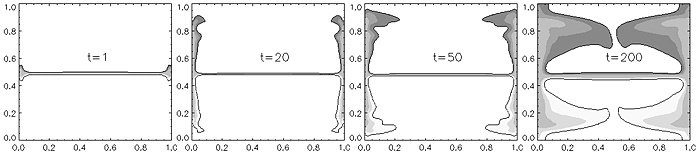
Рис. 30. Динамика распространения примеси
При параметрическом исследовании динамики системы обнаружено, что структура течения существенно зависит от вертикальной составляющей внешнего постоянного силового поля (гравитации). На рис. 31 приведено характерное распределение концентрации для различного уровня гравитации (а: Ra = 1.069·107, б: Ra = 3.563·107).
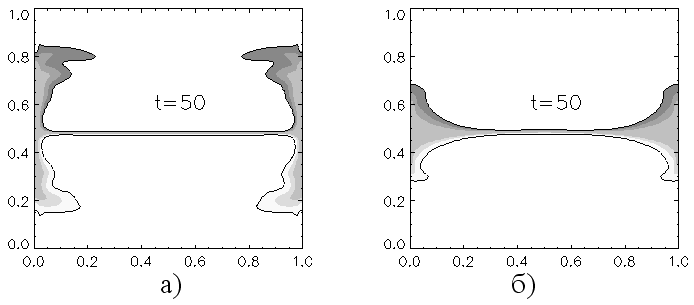
Рис. 31. Характерное распределение концентрации для различного уровня гравитации
В зависимости от параметров задачи обнаружены различные режимы течения. Так, при доминировании вибрационной нагрузки над гравитационной (Gs/Ra > 3, рис. 30, рис. 31 а) наблюдается интенсивный пристенный режим смешивания компонентов с образованием структур течения, характерных для неустойчивости Кельвина-Гельмгольца. Уменьшение интенсивности вибрации приводит к сокращению заброса массы вдоль вертикальных стенок и, в предельном случае, к диффузионному режиму смешивания компонентов (рис. 31 б). Для рассмотренной конфигурации построена диаграмма устойчивости, которая определяет переход от одного режима течения к другому.
При исследовании смешивания слоев различной толщины обнаружены режимы вибрации, при которых происходит растворение только одного из компонентов с сохранением неизменной формы переходной поверхности раздела. На рис. 30 и рис. 32 показано распределение концентрации для случаев, когда координата переходной зоны yc = 0.5, yc = 0.2. Из представленных результатов видно, что в случае смещенной от центра переходной зоны происходит диссипация только одного из компонентов раствора.
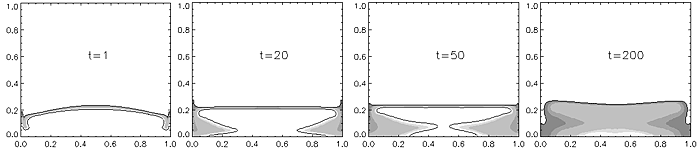
Рис. 32. Распределение концентрации
2. Проведено исследование устойчивости конвективного течения многокомпонент-ной смеси в термогравитационной колонне, когда жидкость находится в вертикальном слое, подогреваемом сбоку (рис. 33). Термодиффузионное разделение смеси между боковыми стенками вместе с вертикальным конвективным потоком приводит к разделению компонентов в вертикальном направлении. Измерение этого разделения в стационарном состоянии позволяет определить коэффициенты термодиффузии. При увеличении разности температур основное конвективное течение может стать неустойчивым.
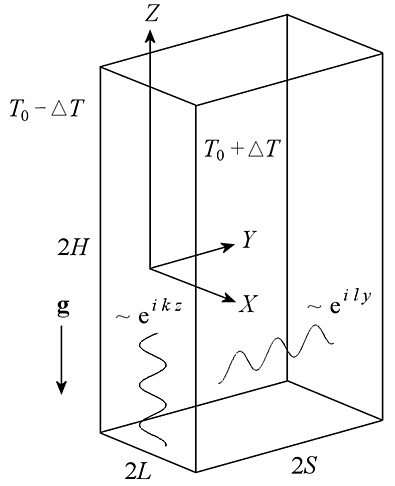
Рис. 33. Геометрия колонны
В рамках линейной теории проведены расчеты критических параметров неустойчивости методом Галеркина, а также методом пошагового интегрирования с ортогонализацией. Впервые исследована устойчивость тройных смесей в колонне. Кроме этого, проведены расчеты для бинарных смесей в широкой области параметров. Исследовались два типа возмущений (рис. 33): продольные волны, распространяющиеся в вертикальном направлении в плоскости, и поперечные волны, распространяющиеся в плоскости. Исследована зависимость критического числа Грасгофа и критических волновых чисел от отношения разделения, которое характеризует термодиффузию (эффект Соре). Расчеты показывают, что для положительных Ψ (в этом случае легкий компонент накапливается около нагретой границы и в верхней части колонны) колебательная мода продольной неустойчивости наиболее опасна. Уменьшение числа Шмидта (т. е. улучшение диффузионных свойств) оказывает стабилизирующий эффект на эту моду. Монотонная мода становится более опасной при приближении Ψ к нулю. Для отрицательных отношений разделения система всегда неустойчива относительно длинноволновых поперечных возмущений. Это связано с тем, что легкий компонент в этом случае накапливается в нижней части слоя, создавая неустойчивую вертикальную стратификацию.
Полученные результаты показывают, что термогравитационная колонна может использоваться для измерения коэффициентов диффузии и термодиффузии в тройных смесях, в которых один из компонентов имеет отрицательных эффект Соре. Также установлено, что уменьшение поперечной длины колонны оказывает стабилизирующий эффект на поперечные возмущения. Результаты данного исследования имеют важное значение при разработке экспериментальных установок и планировании измерений в многокомпонентных системах.
3. С помощью уравнений малых возмущений исследована устойчивость равновесного состояния бинарных смесей с общей поверхностью раздела и одной свободной границей. Нижняя граница системы — неподвижная твердая стенка, верхняя — недеформируемая свободная поверхность. Определяющими параметрами полученной задачи являются числа Марангони, Соре, Вебера, и Био; полагается, что поверхностное натяжение на поверхности раздела и свободной границе линейно зависит от температуры и концентрации.
Построены нейтральные кривые для различных значений числа Соре на поверхности раздела, характеризующего действие эффекта термодиффузии. С усилением термодиффузионного эффекта (рост числа Соре) увеличивается область длинноволновой устойчивости.
Проведенные расчеты показали, что с ростом числа Вебера критические значения числа Марангони уменьшаются, при этом область длинноволновой устойчивости увеличивается.
Основные публикации:
- Андреев В. К., Бекежанова В. Б.
Неустойчивость равновесного состояния жидкости со свободной границей при наличии объёмных источников тепла // МЖГ. — 2008. — № 2. — С. 11-20. - Андреев В. К.
Об одной сопряженной начально-краевой задаче // Дифференциальные уравнения. — 2008. — Т. 44. — № 12. — С. 1667–167 3. - Бекежанова В. Б.
Неустойчивость двухслойной системы при наличии объёмных источников тепла // Вычислительные технологии. — 2008. — Т. 13. — № 4. — С. 24-33. - Andreev V. K., Bekezhanova V. B.
Instability of the Equilibrium State of Liquid with a Free Surface in the Presence of Volume Heat Sources // Fluid Dynamics. — 2008. — Vol. 43. — № 2. — P. 176–184 . - Андреев В. К.
Эволюция совместного движения двух вязких теплопроводных жидкостей в плоском слое под действием нестационарного перепада давления // ПМТФ. — 2008. — Т. 49. — № 4. — С.94–107 . - Родионов А. А., Степанова И. В.
Групповая классификация уравнений модели конвекции с учетом сил плавучести // Вычислительные технологии. — 2008. — Т. 13. — № 5. — С. 61-69.
(Отдел дифференциальных уравнений механики)
| К началу | |