| ИВМ СО РАН | Поиск |
| Отчеты ИВМ СО РАН |
Отчет ИВМ СО РАН за 2003 год
Гранты Российского фонда фундаментальных исследований
- Гранты Российского фонда фундаментальных исследований
- Грант Президента РФ № МК-143.2003.01 — «Молодые кандидаты наук и их научные руководители»
- Грант РФФИ №
02–01–00 934 — «Устойчивость термодиффузионных течений жидкости с поверхностью раздела» - Грант РФФИ № 902.2003.1 — «Ведущие научные школы — «Теория и приложения задач со свободной границей""
- Грант РФФИ №
01–01–00 850 — «Редукции и решения уравнений механики сплошной среды» - Грант РФФИ №
02–01–00 078 — «Бесконечные группы с различными условиями конечности» - Грант РФФИ №
02–01–00 523 — «Математическое и численное моделирование нестационарного распространения импульса энергии большой мощности в вязком теплопроводном газе» - Грант РФФИ №
02–07–90 135 — «Создание Красноярской сети параллельных вычислений» - Грант РФФИ №
03–01–00 081 — «Разработка непараметрических систем классификации множеств случайных величин» - Грант РФФИ №
01–05–65 070 — «Математическая модель магнитосферного магнитного поля» - Грант РФФИ №
03–01–00 218 — «Трехмерное численное моделирование термокапиллярной неустойчивости в тонких слоях жидкости со свободной границей» - Грант РФФИ №
03–07–96 138 р_2003енисей_в — «Геоинформационная интернет-система «Природные ресурсы Красноярского края"" - Грант РФФИ №
03–07–96 139 р2003енисей_в — «Красноярская геоинформационная интернет-лаборатория экологии и регулирования природопользования» - Грант РФФИ №
03–07–06 098 МАС при гранте РФФИ №02–07–90 135 — «Создание Красноярской сети параллельных вычислений» - Грант РФФИ №
03–01–06 474 МАС при гранте РФФИ №02–01–00 523 — «Математическое и численное моделирование нестационарного распространения импульса энергии большой мощности в вязком теплопроводном газе» - Грант РФФИ №
03–05–06 101 МАС при гранте РФФИ №01–05–65 070 — «Математическая модель магнитосферного магнитного поля» - Грант РФФИ №
02–01–11 086 — «Участие в 6-й Европейской конференции по многосеточным методам» - Грант РФФИ №
03–01–10 776 — «Участие в 5-й конференции ЕВРОМЕХ по механике жидкости, Тулуза, Франция, 24-28 августа 2003 г.» - Грант РФФИ №
01–05–64 704 — «Теоретическое и экспериментальное исследование проблемы безопасности приморских территорий на основе оценки рисков сейсмического происхождения методом обратных задач» - Грант РФФИ №
03–01–10 020 — «Организация и проведение II Всероссийской конференции по финансово-актуарной математике и смежным вопросам « - Грант РФФИ №
02–01–07 034 на написание аналитического обзора по группам с условиями конечности
Грант Президента РФ № МК-143.2003.01 — «Молодые кандидаты наук и их научные руководители»
Руководитель:
к.т.н., доцент В. А. Лапко
Разработаны и исследованы новые модификации непараметрических моделей коллективного типа в задаче восстановления временных зависимостей, обеспечивающие более полный, по сравнению с традиционными, учёт информации коротких рядов наблюдений их параметров. Идея предлагаемого подхода состоит в использовании семейства нелинейных упрощенных аппроксимаций и статистических оценок их показателей эффективности при формировании непараметрических коллективов. Полученные теоретические результаты подтверждены данными вычислительного эксперимента и применяются при прогнозировании состояния здоровья населения региона.
Основные публикации:
- Лапко В. А.
Непараметрические коллективы решающих правил. — Новосибирск: Наука. — 2002. — 168 с. - Лапко В. А. Молоков В. В., Лапко А. А.
Модификации непараметрических моделей коллективного типа в задачах восстановления временных процессов // Вестник КрасГАУ. — 2003. — № 3. - Лапко В. А. Соколов М. И., Цугленок Г. И.
Статистические модели электротехнических изделий и процессов с учётом их частичного описания // Вестник КрасГАУ. — 2003. — № 3.
(Отдел вычислительной математики)
| К началу | |
Грант РФФИ №
Руководитель:
д.ф.-м.н., проф. В. К. Андреев
Изучены групповые свойства уравнений неизотермических движений бинарных смесей. При этом используется либо приближение Обербека-Буссинеска, либо микроконвекции. Найдены основные алгебры Ли, оптимальные системы подалгебры первого порядка, а также некоторые точные решения (В. К. Андреев, И. И. Рыжков).
Найдено положение равновесия в модели бинарной смеси, когда плотность в силе плавучести зависит и от давления (В. Б. Бекежанова).
Основные публикации:
- Андреев В. К., Бублик В. В., Бытев В. В.
Симметрии неклассических моделей гидродинамики. — Новосибирск: Наука, 2003. — 352 с. - Андреев В. К.
Задача о малых возмущениях термодиффузионного движения с поверхностью раздела // Препринт № 5. — Красноярск: ИВМ СО РАН, 2002. — 28 с.
(Отдел дифференциальных уравнений механики)
| К началу | |
Грант РФФИ № 902.2003.1 — «Ведущие научные школы — «Теория и приложения задач со свободной границей""
Руководитель:
чл.-корр. РАН В. В. Пухначев
Исполнитель от ИВМ СО РАН:
д.ф.-м.н., проф. В. К. Андреев
Методами группового анализа изучена одна чисто гидродинамическая модель движения воздуха в «глазе» тайфуна. Показано, что в лагранжевой системе координат соответствующую систему можно проинтегрировать в квадратурах. Приведены примеры точных решений модели и дана их метереологическая интерпретация (В. К. Андреев, А. А. Родионов).
Для уравнений термодиффузии найдены оптимальные системы подалгебр 1-го порядка. Выделены подгруппы, относительно которых инвариантны условия на свободной границе и поверхности раздела (В. К. Андреев, И. И. Рыжков).
Проведен групповой анализ вращательно-симметричной модели «глаза» тайфуна. Вычислен базис допустимых операторов. В одном случае построено точное решение.
Для уравнений плоского движения вязкой жидкости в терминах скорость-завихрение в каждом классифицирующем случае функции вязкости ν(t) построены оптимальные системы подалгебр первого порядка (А. А. Родионов).
Основные публикации:
- Родионов А. А.
Групповой анализ и точные решения уравнений плоского движения жидкости в терминах скорость-завихренность // Вычисли-тельные технологии. — 2003. — Т. 8. — № 3. — С. 107–118 . - Андреев В. К., Бублик В. В., Бытев В. В.
Симметрии неклассических моделей гидродинамики. — Новосибирск: Наука, 2003. — 352 с.
(Отдел дифференциальных уравнений механики)
| К началу | |
Грант РФФИ №
Руководитель:
д.ф.-м.н., проф. О. В. Капцов
Введено новое понятие инварианта характеристик для гиперболических систем уравнений с частными производными первого порядка. Даны способы построения новых инвариантов из уже известных. Предложена схема применения инвариантов к редукции и интегрированию систем уравнений с частными производными. Эта схема применялась к одномерным нестационарным уравнениям газовой динамики. Найдены инварианты нулевого и первого порядка для двумерных стационарных уравнений газовой динамики с произвольным уравнением состояния. Доказано, что инварианты должны удовлетворять «уравнениям характеристик», в которых частные производные заменяются на полные.
Основные публикации:
- Kaptsov O. V., Verevkin I. V.
Differential constraints and exact solutions of nonlinear diffusion equations // J. Phys. A: Math. Gen. — 2003. — Vol. 36. — P. 1401–141 4.
(Отдел вычислительных моделей в гидрофизике)
| К началу | |
Грант РФФИ №
Руководитель:
д.ф.-м.н., проф. В. П. Шунков
Охарактеризованы группы с почти слойно конечной периодической частью в классе локально конечных групп и в классе групп без инволюций. Получен признак непростоты для групп, содержащих элемент порядка 3. Для каждого элемента x конечной простой группы G создан, а для групп с небольшим (примерно до миллиона) числом инволюций реализован алгоритм (в системе компьютерной алгебры ГАП), приводящий либо к двум инволюциям, произведение которых равно x, либо к утверждению, что такие инволюции в группе G отсутствуют. Для каждой знакопеременной группы An, n>4, вычислен параметр вложения инволюции.
Созданы компьютерные модели трех (из восьми) выпуклых простых правильногранных тел, которые нельзя получить из платоновых и архимедовых тел сечением тремя или менее плоскостями.
Основные публикации:
- Сенашов В. И., Шунков В. П.
Почти слойная конечность периодической части группы без инволюций // Дискретная математика. — 2002. — Т. 14. — № 3. — С.92–104 . - Сенашов В. И., Созутов А. И., Шунков В. П.
Исследование групп с условиями конечности // Препринт № 2. — Красноярск: ИВМ СО РАН. — 2003. — 97 с.  Тимофеенко А. В.
Тимофеенко А. В.
О порождающих тройках инволюций больших спорадических групп // Дискретная математика. — 2003. — Т. 15. — № 2. — С. 103–112 .
(Отдел дискретной математики)
| К началу | |
Грант РФФИ №
Руководитель:
чл.-корр. РАН В. В. Шайдуров
Для системы уравнений Навье-Стокса вязкого сжимаемого теплопроводного газа разработан новый тип краевых условий, связывающий производные скоростей и давление. Он является естественным для вариационных постановок стационарной и нестационарной задач, т.е. не накладывает дополнительных условий на пространства пробных и тестирующих функций, а учитывается непосредственно в функционалах вариационной постановки. Для проверки применимости этих краевых условий в методе конечных элементов был реализован вычислительный эксперимент для двумерной нестационарной задачи на основе метода Бубнова-Галеркина с кусочно-билинейными базисными функциями. Краевые условия, во-первых, теоретически и практически сохраняли сеточные аналоги балансовых соотношений для энергии, а во-вторых, проявили себя как неотражающие, т.е. они без искажений пропускают возмущения среды из расчетной области наружу без обратного влияния на значения решения внутри области. Это позволяет существенно уменьшить размеры расчетной области для вычислительного анализа локальных явлений, что в конечном итоге служит повышению эффективности вычислительного алгоритма (В. В. Шайдуров, Г. И. Щепановская, Е. Д. Карепова, А. В. Малышев).
Основные публикации:
- Малышев А. В., Шайдуров В. В., Щепановская Г. И.
Повышение точности приближенного решения при расчете плотности в тепловом пятне // Вычислительные технологии. — 2003. — Т. 8. — Региональный вестник Востока. — 2003. — № 3. — (Совм. выпуск. — Ч. 2.) — С. 178–190 . - Шайдуров В. В., Щепановская Г. И.
Математическое и численное моделирование нестационарного распространения импульса энергии большой мощности в вязком теплопроводном газе. Часть 1. Математическая постановка задачи // Красноярск: ИВМ СО РАН. — 2003. — 50 с. (Деп. ВИНИТИ 24.10.03, № 1860-В2003). - Шайдуров В. В., Щепановская Г. И., Малышев А. В.
Расчет плотности в тепловом пятне на многопроцессорной вычислительной системе // Тр. X Междунар. конф. «Математика. Компьютер. Образование». — Москва, Ижевск: НИЦ «Регулярная и хаотическая динамика», 2003. — Вып. 10. — Ч. 2. — С. 234–242 . - Щепановская Г. И.
О влиянии неравномерностей в сверхзвуковом потоке на сопротивление тел// Тез. докл. X Междунар. конф. «Математика. Компьютер. Образование». — Москва, Ижевск: НИЦ «Регулярная и хаотическая динамика», 2003. — Вып. 10. — С. 179.
(Отдел вычислительной математики)
| К началу | |
Грант РФФИ №
Руководитель:
чл.-корр. РАН В. В. Шайдуров
Для двумерной нестационарной системы уравнений Навье-Стокса вязкого сжимаемого теплопроводного газа на основе метода Бубнова-Галеркина с кусочно-билинейными базисными функциями разработано программное обеспечение на многопроцессорной вычислительной системе МВС 1000/16. Проведён анализ коэффициентов ускорения и эффективности построенного алгоритма, в том числе на МВС 1000М Федерального суперкомпьютерного центра с большим числом процессоров. Для ряда вычислительных фрагментов этой задачи, а также для типичных вычислительных фрагментов решения сеточных аналогов задач математической физики в некоторых случаях обнаружено, а затем обосновано сверхлинейное ускорение вычислений, т.е. время вычисления на n процессорах сокращалось более чем в n раз по сравнению с одним процессором, несмотря на дополнительные операции межпроцессорного обмена данными. Причиной сверхлинейного ускорения является увеличение в n раз суммарного объема кэша всех процессоров и, как следствие, гораздо больший объем данных процессоры получают из собственного кэша, а не из оперативной памяти, что в несколько раз медленнее. Прямое подтверждение этой гипотезы получено исчезновением эффекта сверхлинейного ускорения при отключении кэша у процессоров. Построена и подтверждена модель вычислительного процесса с учетом многократного увеличения кэша, в явном виде указывающая условия возникновения сверхлинейного ускорения вычислений при различных соотношениях скоростей вычислений, межпроцессорных обменов и числа процессоров (В. В. Шайдуров, Г. И. Щепановская, Е. Д. Карепова, А. В. Малышев).
Разработано математическое обеспечение на многопроцессорной вычислительной системе МВС 1000/16 для расчета вязких течений со свободной границей с учетом сил поверхностного натяжения и плавучести. Программа реализует решение трехмерных уравнений Навье-Стокса и уравнения теплопроводности с соответствующими краевыми условиями методом частиц для несжимаемой жидкости, разработанного ранее авторами. Эффективность параллельной программной реализации метода исследована на примере задачи о волнах в пленке, стекающей по нагреваемой подложке. На реальных сетках получена эффективность распараллеливания не менее 80 % на 12 процессорах (А. М. Франк, О. А. Судакова).
Проведена Третья межрегиональная школа-семинар «Распределенные и кластерные вычисления», на которой были представлены обзорные лекции и научные сообщения по следующим направлениям:
- проблемы математического моделирования на базе многопроцессорных вычислительных систем;
- параллельные методы декомпозиции в задачах математической физики;
- параллельные вычисления при моделировании динамики сложных дискретных систем;
- проблемы устойчивости распределенных вычислительных задач на кластерах;
- управление параллельными вычислениями;
- проблемы удаленного доступа к вычислительным ресурсам.
Закончено создание оптоволоконной сети Академгородка. Введена в эксплуатацию последняя оптоволоконная линия между ИВМ СО РАН и факультетом иностранных языков Красноярского государственного университета (рис. 1). Со значительным участием средств гранта научного совета
НАТО NIG приобретено активное оборудование для управления оптоволоконной сети Академгородка. В центре города проложена оптоволоконная линия между корпусом «А» Красноярского государственного технического университета и Институтом химии и химической технологии СО РАН (рис. 2). Эта линия позволяет подключить ИХХТ СО РАН без посредников-провайдеров к арендуемому каналу Интернета Красноярск — Новосибирск и информационно-вычислительной сети Академгородка, обеспечив прямой доступ к многопроцессорной вычислительной системе МВС 1000/16 и ряду библиотечных серверов.
Основные публикации:
- Малышев А. В., Шайдуров В. В., Щепановская Г. И.
Повышение точности приближенного решения при расчете плотности в тепловом пятне // Вычислительные технологии. — 2003. — Т. 8. — Региональный вестник Востока. — 2003. — № 3. — (Совм. выпуск. — Ч. 2.) — С. 178–190 . - Шайдуров В. В., Щепановская Г. И., Малышев А. В.
Расчет плотности в тепловом пятне на многопроцессорной вычислительной системе // Тр. X Междунар. конф. «Математика. Компьютер. Образование». — Москва, Ижевск: НИЦ «Регулярная и хаотическая динамика», 2003. — Вып. 10. — Ч. 2. — С. 234–242 . - Щербенин В. Ф., Шайдуров В. В.
Цели и задачи информатизации Красноярска // Материалы VIII Всерос. науч.-практ. конф. «Проблемы информатизации региона». — Красноярск: ИПЦ КГТУ, 2003. — T. 1. — С. 3-8.
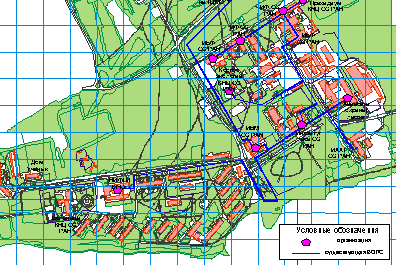
Рис. 1. Схема физических соединений оптоволоконных линий связи Академгородка
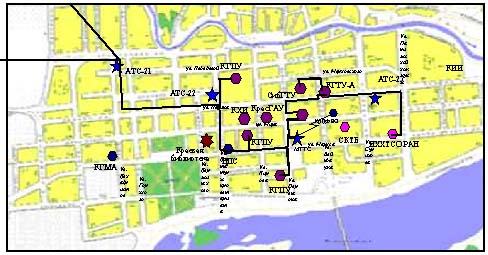
Рис. 2. Схема оптоволоконной сети ВУЗов г. Красноярска (центр города)
(Отдел вычислительной математики)
| К началу | |
Грант РФФИ №
Руководитель:
д.т.н., проф. А. В. Лапко
Впервые обоснована возможность обхода проблем классификации множеств случайных величин путём использования критериев проверки статистических гипотез о тождественности их законов распределения при формировании ядерных мер близости в непараметрических алгоритмах распознавания образов. Полученные результаты обобщены при синтезе структуры непараметрических систем классификации множеств случайных величин при неоднозначных указаниях учителя. Определены условия их асимптотической сходимости и предложены эффективные процедуры оптимизации (А. В. Лапко, В. А. Лапко).
Основные публикации:
- Лапко А. В., Лапко В. А.
Непараметрические модели классификации множеств случайных величин // Информатика и процессы управления. — Красноярск: ИПЦ КГТУ — 2003.
(Отдел вычислительной математики)
| К началу | |
Грант РФФИ №
Руководитель:
д.ф.-м.н., проф. В. В. Денисенко
Построена численная модель возмущения магнитосферного магнитного поля токами в каспах, которые возникают как следствие пересоединения геомагнитного поля с полем, принесенным солнечным ветром (В. В. Денисенко).
Основные публикации:
- Denissenko V. V., Erkaev N. V., Semenov V. S., Biernat H. K., Mezentsev A. V., Zamay S. S.
Erosion of the Magnetopause Caused by the Cusp Currents // Chapman Conference on Physics and modelling of the Inner Magnetosphere. Abstracts. — Finish Meteorological Institute, Helsinki, Finland, 2003. — P. 27.
(Отдел вычислительной математики)
| К началу | |
Грант РФФИ №
Руководитель:
д.ф.-м.н., проф. А. М. Франк
Разработана и программно реализована версия метода частиц для расчета на многопроцессорных ЭВМ течений жидких пленок с учетом эффектов термокапиллярности и плавучести. На реальных сетках получена эффективность распараллеливания не менее 80 % на 12 процессорах. Исследованы некоторые механизмы управления термокапиллярной неустойчивостью в стекающей локально нагреваемой тонкой водяной пленке. Показано, что управляя температурой нагревателя с помощью некоторой обратной связи, можно эффективно подавлять неустойчивость, в том числе в два раза повысить порог возникновения структур.
(Отдел вычислительных моделей в гидрофизике)
| К началу | |
Грант РФФИ №
Руководитель:
д.ф.-м.н., проф. Н. Я. Шапарев
Создан интернет-сайт «Природные ресурсы Красноярского края». На сайте представлены возобновляемые (лес, вода, земли) и невозобновляемые (минеральные ресурсы, полезные ископаемые и т.д.) ресурсы Красноярского края, персоналии, занимающиеся проблемами сохранения и восстановления природных ресурсов.
Основные публикации:
- Шапарев Н. Я., Кадочников А. А., Гостева А. А., Якубайлик О. Э.
Проблемы реализации геоинформационной интернет-системы природно-ресурсной тематики // Тр. науч. конф. «Современные методы математического моделирования природных и антропогенных катастроф. Проблемы защиты населения и территорий от чрезвычайных ситуаций природного и техногенного характера». — Красноярск: ИВМ СО РАН, 2003. — T. 1. — С. 244–250 . - Чеха В. П., Шапарев Н. Я., Якубайлик О. Э., Кадочников А. А.
Геоинформационная Интернет-система «Природные ресурсы Красноярского края» // Вычислительные технологии. — 2003. -Т. 8. — № 12. — (Cпец. выпуск). — C. 86-95. - Гостева А. А., Ерунова М. Г., Якубайлик О. Э.
Технологии подготовки и преобразования картографических данных, связанных с природно-ресурсной тематикой обеспечением // Материалы VIII Всерос. науч.-практ. конф. «Проблемы информатизации региона». — Красноярск: ИПЦ КГТУ, 2003. — T. 1. — С. 82-86.
(Отдел вычислительной физики)
| К началу | |
Грант РФФИ №
Руководитель:
к.ф.-м.н. С. С. Замай
Выполнена разработка технологий геоинформационной Интернет-лаборатории экологии и регулирования природопользования г. Красноярска (С. С. Замай, О. Э. Якубайлик, С. А. Ковязин, А. В. Токарев).
Созданы информационные ресурсы и разработаны программно-технологические основы для моделирования территориально-распределительных экологических процессов в рамках работы геоинформационной интернет-лаборатории (А. Д. Апонасенко, В. В. Денисенко, И. В. Еркаев, С. С. Замай, Ю. Д. Иванова, В. А. Охонин, А. В. Токарев, О. Э. Якубайлик).
Для первоначального наполнения банка геоданных с привязкой к цифровым картам сформированы таблицы баз данных по некоторым оптическим и биологическим характеристикам (в частности, связанным с краснокнижными видами рыб) реки Енисея для разрабатываемой ГИС интернет-лаборатории (А. Д. Апонасенко, С. С. Замай).
Созданы программные компоненты и отработана технология разработки прикладных геоинформационных системы (С. С. Замай, О. Э. Якубайлик, С. А. Артемьев).
Создан прототип ГИС-веб-сервера геоинформационной Интернет-лаборатории экологии и регулирования пприродопользования г. Красноярска (А. В. Беляков, С. С. Замай, А. А. Гостева, М. Г. Ерунова, Ю. Д. Иванова, А. В. Токарев, О. Э. Якубайлик).
Основные публикации:
- Шайдуров В. В., Замай С. С., Якубайлик О. Э.
Технологии и вычислительные модели территориально-ориентированных информационных систем регионального управления и природопользования (Красноярский край) // Вычислительные технологии. — 2003. — Т. 8. — № 12. — (Спец. выпуск). — С. 57-69. - Приложение к Красной книге Красноярского края. Животные / Савченко А. П., Лопатин В. Н., Зырянов А. Н., Смирнов М. Н., Вышегородцев А. А.
- Красноярск: КрасГУ, 2002. — 189 с. - Апонасенко А. Д., Денисенко В. В., Замай С. С., Иванова Ю. Д., Охонин В. А.
Моделирование территориально-распределенных экологических процессов в работе геоинформационной интернет-лаборатории // Материалы VIII Всерос. науч.-практ. конф. «Проблемы информатизации региона». — Красноярск: ИПЦ КГТУ, 2003. — T. 1. — С. 59-65. - Артемьев С. А., Замай С. С., Якубайлик О. Э.
Некоторые вопросы разработки прикладных геоинформационных систем // Материалы VIII Всерос. науч.-практ. конф. «Проблемы информатизации региона». — Красноярск: ИПЦ КГТУ, 2003. — Т. 1. — C. 66-71.
Прототип ГИС-Web-сервера геоинформационной Интернет-лаборатории экологии и регулирования природопользования г. Краснояска http://info.krasn.ru/geoecolab/
(Отдел прикладной информатики, лаборатория биологической спектрофотометрии)
| К началу | |
Грант РФФИ №
Руководитель:
к.т.н. С. В. Исаев
Закончено создание оптоволоконной сети Академгородка. Введена в эксплуатацию последняя оптоволоконная линия между ИВМ СО РАН и факультетом иностранных языков Красноярского государственного университета. Со значительным участием средств гранта научного совета НАТО NIG № 977221 приобретено активное оборудование для управления оптоволоконной сети Академгородка. В центре города проложена оптоволоконная линия между корпусом «А» Красноярского государственного технического университета и Институтом химии и химической технологии СО РАН. Эта линия позволяет подключить ИХХТ СО РАН без посредников-провайдеров к арендуемому каналу Интернета Красноярск — Новосибирск и информационно-вычислительной сети Академгородка, обеспечив прямой доступ к многопроцессорной вычислительной системе МВС 1000/16 и ряду библиотечных серверов.
(Отдел прикладной информатики)
| К началу | |
Грант РФФИ №
Руководитель:
к.ф.-м.н. Е. Д. Карепова
Разработана математическая модель, описывающая двумерные и трёхмерные течения вязкого теплопроводного газа с сильными неоднородностями с новыми естественными краевыми условиями. В двумерном случае построена конечно-элементная дискретизация, удовлетворяющая законам сохранения массы и энергии.
(Отдел вычислительной математики)
| К началу | |
Грант РФФИ №
Руководитель:
И. Л. Аршукова
На основе МГД модели были исследованы возможность развития перестановочной неустойчивости и условия ее возникновения на границе ионосферы Венеры с учетом эффекта загрузки масс. Показано, что возмущения, вызываемые перестановочной неустойчивостью, локализованы в пределах ионопаузы и магнитного барьера и не проникают в смежную с ударной волной часть переходного слоя (И. Л. Аршукова).
Основные публикации:
- Biernat H. K., Erkaev N. V., Arshukova I. L., Lammer H., Penz T., Vogl D. F., Zhang T. L., Baumjohann W.
MHD effects as a cosequence of the solar wind surrounding Venus and Mars // Abstr. of the 26 th Annual Seminar on Physics of auroral phenomena. — Apatity, 2003. — P. 41.
(Отдел вычислительной математики)
| К началу | |
Грант РФФИ №
Руководитель:
чл.-корр. РАН В. В. Шайдуров
По этому гранту состоялась командировка В. В. Шайдурова в г. Хоэнварт (Германия) с 6 по 11 октября 2002 г. для участия в 6-й Европейской конференции по многосеточным методам. Сделан доклад «Многосеточные методы для сеточных задач конвекции-диффузии».
(Отдел вычислительной математики)
| К началу | |
Грант РФФИ №
Руководитель:
д.ф.-м.н., проф. А. М. Франк
По этому гранту состоялась командировка А. М. Франка в г. Тулуза (Франция) для участия в конференции EFMC2003. Конференция проводится раз в три года под эгидой общества EUROMECH (European mechanics society). Предыдущие были в Кембридже (1991), Варшаве (1994), Геттингене (1997) и Эйндховене (2000). Конференция собирает ведущих европейских специалистов в этой области, а также ученых с других континентов, и является крупнейшим европейским форумом по механике жидкости. На конференции этого года было представлено 9 пленарных лекций, около 350 устных докладов и около сотни стендовых. Сделан устный доклад «Трехмерное численное исследование регулярных структур в локально нагреваемой пленке жидкости».
(Отдел вычислительных моделей в гидрофизике)
| К началу | |
Грант РФФИ №
Руководитель:
д.ф.-м.н., проф. М. М. Лаврентьев мл
Исполнитель от ИВМ СО РАН:
к.ф.-м.н. К. В. Симонов
Разработана вычислительная технология для анализа данных регистрации цунами и решения обратной задачи цунами в режиме реального времени на основе нелинейной многопараметрической регрессии с целью прогноза цунамиопасности.
Основные публикации:
- Lavrentiev M. M., Jr., Simonov K. V.
Stochastic resonance in application to tsunamigenic of underwater earthquake // Proc. of the Int. Symp. «Topical problems of nonlinear wave physics». NWP-3. — Nizhny Novgorod: IAP RAS, 2003. — Р. 268–269 .
(Отдел вычислительных моделей в гидрофизике)
| К началу | |
Грант РФФИ №
Руководитель:
д.ф.-м.н., проф. О. Ю. Воробьев
Проблемы принятия решений в экономике, в финансовом и актуарном деле представляют постоянный интерес для научного исследования в самых различных и иногда неожиданных областях науки. Данный вывод подтверждается статьями и докладами, представленными на II Всероссийской ФАМ'2003 конференции. В настоящее время сформировалось направление работы ФАМ конференций, которое постепенно втягивает в свою сферу научные интересы участников из многих смежных областей математики. В пределах этого направления работа II Всероссийской ФАМ конференции проводилась параллельно по пяти секциям, которые охватили следующие темы: финансово-актуарная математика; эвентология и теория случайных событий; дискретная математика и теория случайных множеств; системный анализ, управление и обработка случайных событий; теория вероятностей и математическая статистика; математическая теория потребностей, полезностей и рисков; теория игр случайных коалиций; математическое моделирование зависимостей и взаимодействий событий в статистических системах природы и общества; применение эвентологии и математических методов (экономика, финансы, страхование, медицина, экология, социология, этнология, психология, педагогика, политология). В программу конференции были включены 102 доклада 122 ученых из 15 городов. К началу конференции был издан сборник тезисов всех представленных докладов. Непосредственно в работе конференции приняло участие 77 человек, из них 20 кандидатов и докторов наук, 37 студентов и аспирантов. Было заслушано 14 пленарных докладов и 41 секционных.
В рамках конференции состоялись заседания 5 секций:
- Статистическая эвентология и теория случайных событий (пред. — проф. Воробьев О. Ю.);
- Финансово-актуарная математика (пред. — проф. Григорьев Ю. Д.);
- Вероятность, статистика и теория риска (пред. — Новоселов А. А.);
- Статистические системы природы и общества (пред. — проф. Гуц А. К.);
- Математическое моделирование в медицине и здравоохранении (пред. — проф. Савченко А. А., проф. Мажаров В. Ф.).
Принято решение о проведении III Всероссийской ФАМ конференции в марте 2004 года в г. Красноярске.
Основные публикации:
Тезисы докладов II Всероссийской конференции по финансово-актуарной математике и смежным вопросам / Под ред. Д. В. Семеновой. — Красноярск: КГУ, 2003. — 117 с.
Труды II Всероссийской конференции по финансово-актуарной математике и смежным вопросам. Ч. 1. / Под ред. О. Ю. Воробьева. — Красноярск: ИВМ СО РАН, 2003, — 299 с. (ISBN 5-85981–044 -X).
Труды II Всероссийской конференции по финансово-актуарной математике и смежным вопросам. Ч. 2. / Под ред. О. Ю. Воробьева. — Красноярск: ИВМ СО РАН, 2003, — 299 с. (ISBN 5-85981–043 -1).
(Отдел дискретной математики)
| К началу | |
Грант РФФИ №
Руководитель:
д.ф.-м.н., проф. В. П. Шунков
Авторы:
В. И. Сенашов, А. И. Созутов, В. П. Шунков
В обзор вошли результаты известной как у нас в стране, так и за рубежом алгебраической школы, руководимой профессором В. П. Шунковым. Школа включает в себя следующие направления исследований: группы Фробениуса, строение групп Фробениуса и некоторых расщепляемых групп, признаки непростоты бесконечных групп, локально разрешимые группы, локально конечные группы, слойно конечные группы, почти слойно конечные группы, черниковские группы, обобщенно черниковские группы, счетные группы, группы конечного ранга, группы с конечными элементами, финитно-аппроксимируемые группы, бесконечные группы с сильно вложенной подгруппой, группы с условием минимальности, группы с условием минимальности для абелевых подгрупп, группы с условием примарной минимальности, группы, насыщенные конечными простыми неабелевыми группами, T0-группы, Mp-группы, Ф-группы. В обзоре процитировано 250 работ российских и зарубежных ученых. Объем обзора 36 страниц. Обзор сдан в РФФИ.
(Отдел дискретной математики)
| К началу | |