| ИВМ СО РАН | Поиск |
| Отчеты ИВМ СО РАН |
Отчет ИВМ СО РАН за 2009 год
Интеграционные, экспедиционные проекты, гранты СО РАН
- Заказные интеграционные проекты
- Междисциплинарные интеграционные проекты
- Проект № 26 «Математические модели, численные методы и параллельные алгоритмы для решения больших задач СО РАН и их реализация на многопроцессорных суперЭВМ»
- Проект № 31 «Теоретическое и экспериментальное изучение путей повышения эффективности, надежности и долговечности импульсных машин для разрушения горных пород и изменения свойств породного массива»
- Проект № 40 «Термодинамические согласованные модели сплошных сред и их вычислительное моделирование: вычислительные модели, алгоритмы и их программная реализация; новые критерии устойчивости движения, позволяющие указывать допуски на определяющие параметр
- Проект № 50 «Модели изменения биосферы на основе баланса углерода (по натурным и спутниковым данным и с учетом вклада бореальных экосистем)»
- Проект № 65 «Теоретико-групповые и геометрические методы исследования нелинейных моделей механики сплошных сред и математической физики: точные решения, интегрируемость, сигулярности»
- Проект № 95 «Комплексные исследования механизмов стратификации биологических, химических и физических компонент водных экосистем как основа для прогноза и управления качеством воды»
- Проект № 116 «Антропогенные риски угледобывающих и нефтегазодобывающих территорий Сибири»
- Проекты, выполняемые совместно со сторонними научными организациями
- Экспедиционные проекты
- Целевые программы СО РАН
Междисциплинарные интеграционные проекты
Проект № 26 «Математические модели, численные методы и параллельные алгоритмы для решения больших задач СО РАН и их реализация на многопроцессорных суперЭВМ»
Руководитель: академик Б. Г. Михайленко
Ответственный исполнитель от ИВМ СО РАН: к.ф.-м.н., доцент Е. Д. Карепова
1. Математическое моделирование. Рассмотрена математическая модель, описывающая в двумерных по пространству и нестационарных по времени постановках трансформацию стока талых и дождевых вод речным бассейном и русловую трансформацию при заданных расходах воды во входном и замыкающем створах исследуемого участка речной системы. В качестве исходной математической модели рассмотрены уравнения мелкой воды.
Описанная физико-математическая модель, в отличие от развитых одномерных моделей (уравнения Сен-Венана, кинематической волны и др.), более тщательно учитывает рельеф русла и поверхности водосбора и водостока, что особенно важно для прогноза половодья. Конечно, для практических целей в модели следует уточнить множество параметров водостока различных поверхностей; это будет сделано уже в процессе ее использования. С математической точки зрения сформулированная задача является замкнутой и обеспеченной устойчивостью решения благодаря невозрастанию энергии течения.
Модель будет служить базисом для математической модели трансформации стока с учетом талых и дождевых вод на территории водосбора, ограниченной водоразделом и гидроэлектростанциями. Рекомендованы комбинации краевых и начальных условий, обеспечивающие однозначную разрешимость задачи. Рассмотрено применение полностью неявной разностной схемы по времени с применением итераций по нелинейностям на каждом временном слое.
2. Формирование базы данных натурной информации для численных экспериментов. Для сравнения численных экспериментов и наблюдений сформирован банк натурных данных, в том числе по материалам отчетов 1959 г. о проведении масштабных экспериментов по изучению неустановившегося движения на р. Тверцы.
3. Расчеты на высокопроизводительных вычислительных системах. Для разработанных параллельных алгоритмов численного решения краевой задачи для уравнений мелкой воды проведено исследование их ускорения и эффективности в зависимости от количества процессов, способа реализации коммуникаций (блокирующие, неблокирующие передачи), способа декомпозиции вычислительной области, архитектуры суперЭВМ.
Основу параллельного алгоритма составляет параллельное решение системы линейных алгебраических уравнений для реальных акваторий, имеющих большую размерность. Для решения таких систем использовался итерационный метод Якоби, который обладает хорошим параллелизмом, а диагональное преобладание для его сходимости легко обеспечивается выбором шага по времени.
Используя явный параллелизм по данным, исходную расчетную область можно разбить на несколько частично перекрывающихся подобластей. Расчеты в каждой подобласти выполняются независимо друг от друга в рамках итерации Якоби. После каждой итерации Якоби необходимо проводить согласование данных в перекрытиях. Реализованы два варианта разбиения, которые были алгоритмически разработаны и программно реализованы для равномерной триангуляции прямоугольной области на сфере.
Реализация параллельной программы осуществлялась на языке программирования Си с применением функций библиотеки передачи сообщений MPI. Вычислительный эксперимент был проведен на трех высокопроизводительных комплексах.
Во-первых, вычисления выполнялись на 99-ядерном кластере ИВМ СО РАН (собственная сборка ИВМ СО РАН, содержит однопроцессорные одноядерные, однопроцессорные двуядерные и двухпроцессорные двуядерные вычислительные узлы, соединенные сетью передачи данных GigaEthernet). Вторым кластером, на котором проведены серии расчетов, является кластер МВЦ ТГУ СКИФ Cyberia, который содержит 283 двухпроцессорных двуядерных вычислительных узла (1132 ядра), объединенных высокопроизводительной сетью передачи данных InfiniBand. Наконец, эксперименты были частично повторены на высокопроизводительном вычислительном комплексе ИВЦ НГУ, на базе кластера, основанного на блэйд-серверах Hewlett-Packard BL460c из 64 восьмиядерных вычислительных узлов, объединенных высокопроизводительной сетью InfiniBand. Отличительной чертой первого кластера, является его гетерогенная архитектура. Кластер SKIF Cyberia и HP-кластер ИВЦ НГУ отличаются в интересующем нас плане только количеством ядер на узел.
На рис. 35 представлена зависимость ускорения вычислений от количества используемых процессов для мелкой сетки, полученных на кластерах ИВМ СО РАН и SKIF Cyberia. Для сравнения представлен график потенциального ускорения согласно теоретическим оценкам. В экспериментах на кластере ИВМ СО РАН общий тренд ускорения совпадает с теоретическими оценками, однако его рост носит сильно неустойчивый характер. Расчеты, проведенные на кластере СКИФ Cyberia, показывают классическую картину ускорения, подтверждающую линейный характер его роста с увеличением количества процессоров с эффективностью около единицы (эффективность расчета для 32 узлов ≈ 0.85 ). Неустойчивый характер ускорения в расчетах, проведенных на кластере ИВМ СО РАН, объясняется, скорее всего, его неоднородной архитектурой. Отметим, что тип декомпозиции существенно не влияет на ускорение параллельной программы, а неблокирующие операции следует признать более надежными и эффективными.
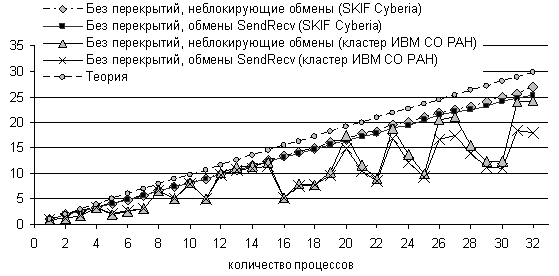
Рис. 35. Зависимость ускорения вычислений от количества доступных процессоров. Сетка 801 801
Поскольку время выполнения программы складывается из времени вычислений, времени коммуникаций и дополнительного времени для операций, связанных с распределенностью данных, то были проведены серии расчетов, в которых эти составляющие были измерены отдельно. На рис. 36 приведены результаты этих экспериментов для случая декомпозиции без перекрытий и неблокирующего режима двухточечных обменов.
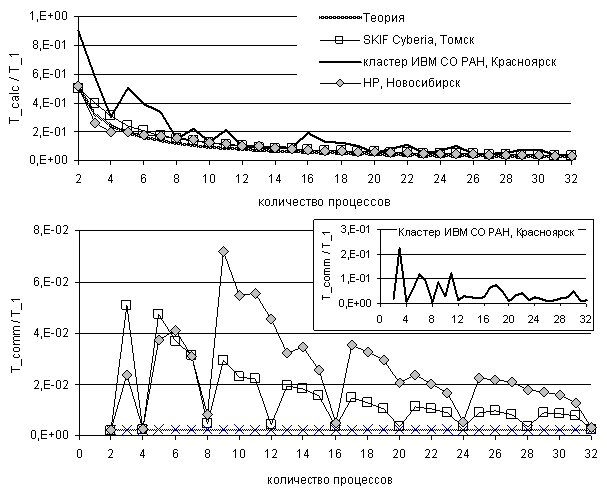
Рис. 36. Исследование времени, затраченного на вычисления и коммуникации
Неблокирующие обмены, декомпозиция без теневых граней
Время на дополнительные операции не зависит от количества участвующих в вычислениях процессов и на пять-шесть порядков меньше суммарного времени вычислений и коммуникаций. Время выполнения вычислений (рис. 36) для гомогенных архитектур совпадает с теоретическими оценками. Ввиду неоднородности узлов кластера ИВМ СО РАН время вычислений в этом случае уменьшается немонотонно.
Время выполнения обменов в неблокирующем режиме теоретически не должно зависеть от количества процессов, участвующих в расчетах. Для кластера с неоднородной архитектурой наблюдается ожидаемое немонотонное поведение исследуемой величины. Однако немонотонное поведение наблюдается и в случае расчетов для гомогенных архитектур. Исследование времени выполнения обменов показало следующее: 1) время обменов минимально и не зависит от количества процессов, участвующих в обменах, если загружены все ядра на узле по одному процессу на ядро (для SKIF Cyberia количество процессов кратно четырем, для HP-кластера ИВЦ НГУ — восьми)); 2) при существовании в расчетах узлов, не полностью загруженных, время обменов тем больше, чем больше количество простаивающих ядер; 3) время, затраченное на обмены, уменьшается с ростом количества задействованных процессов (т.е. уменьшением времени вычислений).
По результатам исследований было сделано 7 докладов на международных и всероссийских конференциях, опубликовано 5 работ в журналах и материалах конференций, еще 5 работ принято к печати.
Основные публикации:
- Карепова Е. Д., Шайдуров В. В., Вдовенко М. С.
Параллельные реализации метода конечных элементов для краевой задачи для уравнений мелкой воды // Вестник ЮУрГУ. Серия «Математическое моделирование и программирование». — 2009. — Вып. 3. — № 17 (150). — С. 73-85. - Карепова Е. Д., Шайдуров В. В., Вдовенко М. С.
Параллельные реализации метода конечных элементов для краевой задачи для уравнений мелкой воды // Материалы IV Междунар. конф. «Параллельные вычислительные технологии». — Н. Новгород. — 2009. — С. 205–217 . - Карепова Е. Д., Шайдуров В. В.
Исследование эффективности параллельных реализаций МКЭ для краевой задачи для уравнений мелкой воды // Тез. докл. междунар. конф. «Математика в приложениях». — Новосибирск: ИМ СО РАН. — 2009. — С. 136–137 . - Karepova E. D., Malyshev A. V., Shaidurov V. V.
Research of efficiency of parallel realization of FEM for Boundary problem of shallow water equation // Тез. докл. междунар. конф. «Математические и информационные технологии». Копаоник (Сербия), Будве (Черногория) 2009. — С. 75-76. - Карепова Е. Д.
Численное моделирование поверхностных волн в больших акваториях // Материалы семинара ИВМ СО РАН «Проблемы математического и численного моделирования». Вычислительные технологии. — 2009. — Т. 14. — № 1. — С. 28-29. - Карепова Е. Д., Шайдуров В. В.
Параллельная реализация МКЭ для начально-краевой задачи мелкой воды // Вычислительные технологии. — 2009. — Т.14, № 6. — С. 45-57. - Шайдуров В. В., Карепова Е. Д.
Двумерная нестационарная математическая модель речного стока и водосбора // Материалы междунар. конф. «Математические и информационные технологии». — Копаоник (Сербия), Будве (Черногория). — 2009. — 4 с. (в печати). - Карепова Е. Д., Шайдуров В. В.
Исследование эффективности параллельных реализаций МКЭ для начально-краевой задачи для уравнений мелкой воды // Материалы междунар. конф. «Математические и информационные технологии». — Копаоник (Сербия), Будве (Черногория). — 2009. — 10 с. (в печати).
(Отдел вычислительной математики)
| К началу | |
Проект № 31 «Теоретическое и экспериментальное изучение путей повышения эффективности, надежности и долговечности импульсных машин для разрушения горных пород и изменения свойств породного массива»
Руководитель: д.т.н., профессор Б. Н. Смоляницкий
Ответственный исполнитель от ИВМ СО РАН: к.т.н., доцент С. В. Доронин
Этап 2009 — Исследование напряжений при различных параметрах ударного нагружения и сопротивления ударно-усталостному разрушению соударяющихся деталей. Оценка влияния скорости удара на передачу энергии к рабочему органу (инструменту).
Выполнена верификация результатов моделирования напряженно-деформированного состояния деталей ударных систем с экспериментальными данными и результатами аналитических расчетов. Показан достаточный уровень точности результатов моделирования.
При решении модельной задачи соударения двух тел, геометрические размеры, массы и скорости которых соответствуют таковым для деталей погружных пневмоударников, получены зависимости максимальных эквивалентных напряжений и пластических деформаций от скорости соударения, максимальных пластических деформаций и времени соударения от радиуса закругления торца бойка, максимальных эквивалентных напряжений, пластических деформаций и времени соударения от модуля Юнга материала деталей.
Решена контактная динамическая задача соударения бойка и ряда коронок типоразмерного ряда погружных пневмоударников (рис. 37).
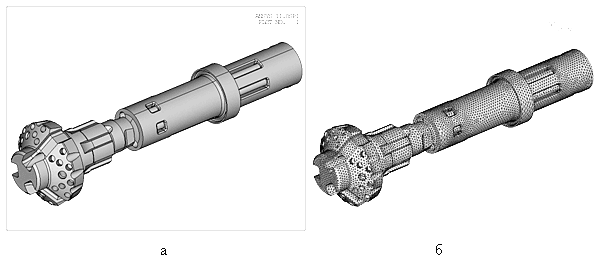
Рис. 37. Твердотельные (а) и конечно-элементные (б) модели коронки и бойка
Выполнено исследование характера распределения полей интенсивности напряжений при ударном взаимодействии деталей (рис. 38).
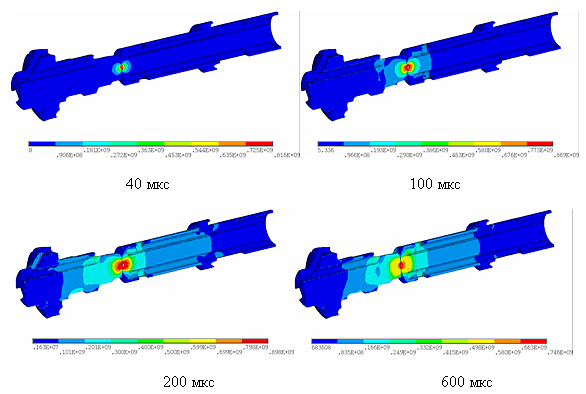
Рис. 38. Распределение интенсивности напряжений (Па) в продольном сечении бойка и коронки при их ударном взаимодействии в различные моменты времени
Для различных параметров ударного нагружения получены расчетные осциллограммы напряжений в характерных конструктивных зонах и сечениях деталей (рис. 39).
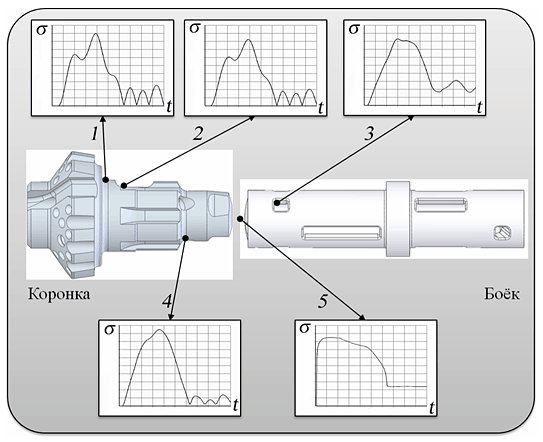
Рис. 39. Осциллограммы напряжений при соударении бойка и коронки ø 180 мм
Разработана и практически реализована методика оценки при ударно-циклическом нагружении.
Основные публикации:
- Доронин С. В., Косолапов Д. В.
Моделирование напряженно-деформированного состояния и оценка ресурса при ударно-циклическом нагружении // Вестник СибГАУ. — 2009. — Вып. 1 (22). — Ч. 2. — С. 23-27. - Доронин С. В., Косолапов Д. В.
Напряженно-деформированное состояние деталей машин импульсного действия // Тяжелое машиностроение. — 2009. — № 6. — С. 25-27. - Доронин С. В., Косолапов Д. В.
Расчетное обоснование модернизации деталей импульсных машин // Ремонт, восстановление, модернизация. — 2009. — № 7. — С. 24-29. - Доронин С. В., Косолапов Д. В.
Оценка ресурса деталей машин импульсного действия // Вестник машиностроения. — 2009. — № 7. — С. 21-26. - Косолапов Д. В., Доронин С. В.
Задачи вычислительного моделирования при проектных расчетах деталей машин импульсного действия // Материалы IV Междунар. конф. «Проблемы механики современных машин». — Улан-Удэ: ВСГТУ. — 2009. — Т. 3. — С. 65-68.
(Отдел машиноведения)
| К началу | |
Проект № 40 «Термодинамические согласованные модели сплошных сред и их вычислительное моделирование: вычислительные модели, алгоритмы и их программная реализация; новые критерии устойчивости движения, позволяющие указывать допуски на определяющие параметры»
Руководитель: академик РАН С. К. Годунов
Ответственный исполнитель от ИВМ СО РАН: д.ф.-м.н., профессор В. М. Садовский
Система уравнений динамики моментного континуума Коссера, описывающая распространение упругих волн в средах с микроструктурой, приведена к самосогласованной системе законов сохранения, которая совпадает с симметрической формой записи системы, гарантирует гиперболичность и позволяет применить к ее исследованию эффективные численные методы, адаптированные к расчету обобщенных решений с разрывами, вызванными сосредоточенными и импульсными воздействиями. Аналогичная форма получена для линейной системы уравнений динамики редуцированного континуума с равным нулю тензором моментных напряжений. На этой основе получен общий вид математически корректной постановки начальных и граничных условий, а также условий симметрии при решении краевых задач. Разработаны эффективные алгоритмы для численного исследования модели на многопроцессорных вычислительных системах.
С помощью спектрально-разностного метода в одномерной постановке выполнено численное решение задачи о циклическом сдвиге вязкоупругого слоя. По результатам расчетов определена частота собственного резонанса моментной среды, связанная с вращательными колебаниями частиц. В рамках модели пространственного напряженно-деформированного состояния проведен численный анализ колебательных процессов, результаты которого подтвердили, что в средах с микроструктурой существует характерная резонансная частота, соответствующая частоте собственных колебаний вращательного движения. Показано, что эта частота зависит только от инерционных свойств частиц микроструктуры материала и не зависит от размеров исследуемой области и граничных условий на ее поверхности. На рис. 40 приведены поверхности уровня угловой скорости частиц для нерезонансного (слева) и резонансного (справа) нагружений вращательным моментом. Расчеты показали, что при частоте внешнего воздействия, равной собственной частоте вращательного движения частиц, происходит рост амплитуды со временем и более плавное затухание колебаний с удалением от точки приложения нагрузки, характерное для акустического резонанса.
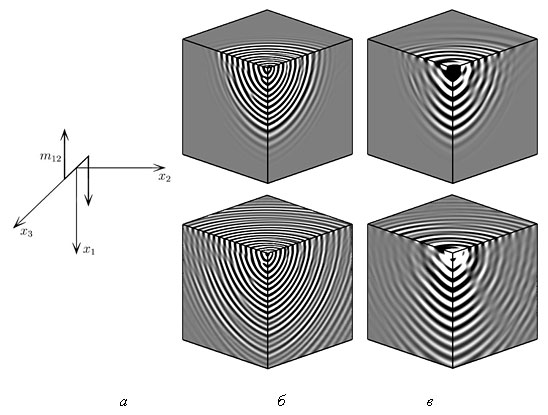
Рис. 40. Схема нагружения (а) и поверхности уровня угловой скорости ω2 для нерезонансной (б) и резонансной (в) частот в различные моменты времени (вверху t = 6,5 мкс, внизу t = 13 мкс)
Сделан детальный обзор основных современных результатов по полиномиальной интерполяции Лагранжа по заданным узлам и узловым значениям для функции, определённой на отрезке и обладающей достаточной гладкостью. Особо выделен случай, когда концы отрезка являются и узлами интерполяции, что присуще МКЭ. Получены выражения для погрешности лагранжевой интерполяции в интегральной форме. Если же на одном или двух концах отрезка известны значения производной аппроксимируемой функции, то получены детальные соотношения для интерполяции Лагранжа-Эрмита и соответствующие выражения для погрешностей. Предложен алгоритм вычисления значения простейшего линейного интегрального функционала на решении первой краевой задачи для обыкновенного дифференциального уравнения второго порядка. Показано, что можно последовательно получать значения интегрального функционала с любой наперёд заданной точностью, не вычисляя самого решения.
Основные публикации:
- Садовская О. В.
Численное решение пространственных динамических задач моментной теории упругости с граничными условиями симметрии // Журнал вычислительной математики и математической физики. — 2009. — Т. 49. — № 2. — С. 313–322 . - Варыгина М. П., Садовская О. В., Садовский В. М.
Численное моделирование пространственных волновых движений в моментной упругой среде // I Всерос. конф. «Проблемы механики и акустики сред с микро- и наноструктурой: НАНОМЕХ-2009». — Н. Новгород. — 2009. — С. 39-51. (CD-диск). - Варыгина М. П., Садовская О. В., Садовский В. М.
Численное решение пространственных динамических задач моментной теории упругости // Тр. XVI Зимней школы по механике сплошных сред. — Пермь: Ин-т мех. сплошных сред УрО РАН. — 2009. — 5 с. (CD-диск). - Киреев И. В.
Лагранжево-эрмитова аппроксимация функций одной переменной // Препринт № 3. — Красноярск: ИВМ СО РАН. — 2009. — 31 с.
(Отдел вычислительной механики деформируемых сред)
| К началу | |
Проект № 50 «Модели изменения биосферы на основе баланса углерода (по натурным и спутниковым данным и с учетом вклада бореальных экосистем)»
Координатор проекта: академик Е. А. Ваганов, член-корреспондент РАН А. М. Федотов
Ответственный исполнитель от ИВМ СО РАН: д.ф.-м.н., профессор В. М. Белолипецкий
Предложен метод для определения потока СО2 (QC), использующий одномерную и точечную модели для концентраций углекислого газа в атмосфере и измеренные на высоких вышках профили концентраций в атмосфере. Для вычисления коэффициента вертикального обмена в приземном слое атмосферы предлагаются соотношения, полученные с использованием формулы Прандтля-Кармана, оценки толщины пограничного слоя и логарифмического закона вертикального распределения скорости ветра.
Выделяются два характерных периода: «день» и «ночь». К ночному периоду отнесены данные, в которых наблюдается поток СО2 из наземного слоя в атмосферу, к дневному — когда поток СО2 из атмосферы к поверхности Земли. Оцениваются средние значения QC днем и средние значения QC ночью. По найденным значениям вычисляется среднесуточный поток.
Выполнены пробные расчеты с использованием данных измерений на вышке, взятых с сервера ftp://ftp.cmdl.noaa.gov/ccg/towers/.
Результаты работы были представлены на Национальной конференции «Математическое моделирование в экологии», г. Пущино, 2009 и на X Всероссийской конференции «Проблемы мониторинга окружающей среды», г. Кемерово, 2009.
Основные публикации:
- Белолипецкий П. В.
Оценка потока углерода между атмосферой и наземной экосистемой по измерениям СО2 на высоких вышках // Материалы Национальной конф. «Математическое моделирование в экологии». — Пущино: ИФХиБПП РАН. — 2009. — С. 33.
(Отдел вычислительных моделей в гидрофизике)
| К началу | |
Проект № 65 «Теоретико-групповые и геометрические методы исследования нелинейных моделей механики сплошных сред и математической физики: точные решения, интегрируемость, сигулярности»
Координаторы проекта: академик РАН Л. В. Овсянников, член-корреспондент РАН И. А. Тайманов
Блок ИВМ СО РАН «Исследование инвариантных подмоделей неклассических уравнений конвекции»
Ответственный исполнитель: д.ф.-м.н., профессор В. К. Андреев
1. Для системы трехмерных уравнений модели конвекции с учетом эффекта Соре и в случае уравнения состояния общего вида решена задача групповой классификации относительно функции R(θ,c), определяющей силу плавучести и нелинейно зависящей от малого отклонения температуры, концентрации легкой компоненты, от их средних значений. Результат исследования представлен в виде таблицы, где выписана 41 специализация классифицируемой функции и операторы, допускаемые исследуемой системой в зависимости от найденных специализаций. При составлении этих таблиц существенно использовались преобразования эквивалентности, вычисленные ранее и позволившие существенно упростить вид классифицируемой функции. Тем самым выделились степенные, логарифмические и экспоненциальные зависимости силы плавучести от заданных параметров. Следует отметить, что степенные зависимости силы плавучести от температуры и концентрации широко применяются в расчетах, где уравнение состояния жидкости определяется экспериментальным путем.
2. В рамках проекта была исследована модель вибрационной конвекции бинарной смеси с помощью теоретико-групповых методов. Вибрационной конвекцией называют специальные течения, которые возникают в жидкости с градиентом плотности под действием внешней вибрации. В бинарной смеси градиент плотности может быть вызван градиентами температуры и концентрации. В случае высоких частот течение можно условно разделить на две составляющие: «быструю», которая осциллирует с частотой внешнего воздействия, и «медленную», осредненную по времени часть, которая характеризует нелинейные взаимодействия в жидкости под действием периодической внешней силы.
3. Построено решение системы уравнений термодиффузионной конвекции в случае стационарного однонаправленного вертикального течения жидкости между двумя твердыми стенками под воздействием градиента давления φ0 и функции, отвечающей за силу плавучести R. Такое решение инвариантно относительно операторов δt, δy, δz + φ0δp, где p — модифицированное давление. На твердых стенках x = −l, x = l заданы температура θ1 и θ2, условие отсутствия потока вещества через твердые стенки, а также условия прилипания. Были рассмотрены две возможности для представления силы плавучести: экспоненциальная и степенная зависимости от разности двух инвариантных функций, соответствующих физическим температуре и концентрации. Следует отметить, что в обоих случаях течение отличается от хорошо известного течения Пуазейля с параболическим профилем скоростей, существенный вклад в развитие течения дает сила плавучести. Выражения для температуры и концентрации в обоих случаях одинаковы и представляют собой линейные зависимости от координаты x.
4. Проведена групповая классификация модели осредненных движений бинарной смеси под действием вибрации. Найдены алгебры Ли операторов, допускаемые системой в зависимости от значений постоянных параметров, входящих в уравнения.
5. Доказаны интегральные неравенства типа Фридрихса для составных областей при наличии плоской и цилиндрической симметрии. Найдены оптимальные постоянные, входящие в правые части неравенства. Этот результат позволил получить оценки скорости сходимости нестационарных однонаправленных течений бинарных смесей в плоских и цилиндрических слоях к стационарным режимам.
Основные публикации:
- Андреев В. К., Бекежанова В. Б., Ефимова М. В., Рыжков И. И., Степанова И. В.
Неклассические модели конвекции: точные решения и их устойчивость // Вычислительные технологии. — 2009. — Т. 14. — № 6. — С. 5-18. - Андреев В. К., Степанова И. В.
Симметрия уравнений термодиффузии при нелинейной зависимости силы плавучести от температуры и концентрации // Вычислительные технологии (направлена в печать). - Андреев В. К.
О неравенстве типа Фридрихса для составных областей // J. of Siberian Federal University. Mathematics and Physics. — 2009. — № 2(2). — P. 146–157 . - Андреев В. К.
О совместном однонаправленном движении двух вязких теплопроводных жидкостей в трубе // ПМТФ. — 2009 (направлена в печать).
(Отдел дифференциальных уравнений механики)
| К началу | |
Проект № 95 «Комплексные исследования механизмов стратификации биологических, химических и физических компонент водных экосистем как основа для прогноза и управления качеством воды»
Координатор проекта: член-корреспондент РАН А. Г. Дегерменджи
Ответственный исполнитель от ИВМ СО РАН: д.ф.-м.н., профессор В. М. Белолипецкий
Важными элементами вертикальной гидрофизической структуры соленого озера являются термоклин (Т), халоклин (S) и пикноклин (ρ), в которых наблюдаются наибольшие изменения по вертикали температуры, солености и плотности воды. Меромиктические озера представляют собой относительно немногочисленный тип озер с устойчивой пространственной гетерогенностью, которая создает особые условия формирования биогеохимического круговорота веществ. Озеро представляется в виде двухслойной системы эпилимниона (верхнего слоя) и гиполимниона (нижнего слоя). Ключевым отличием озер данного типа от других водоемов является наличие постоянного анаэробного слоя водной толщи, в котором развивается сульфидогенная микрофлора. В зоне халоклина создаются условия для локального круговорота биогенных элементов, осуществляемого специфической микрофлорой. Вертикальная плотностная стратификация оказывает решающее влияние на пространственно-временные распределения химических компонент и экологию планктонных организмов в глубоких озерах.
В водной толще стратифицированных водоемов формируются экологически значимые вертикальные градиенты температуры, света, кислорода, солености, редокс-потенциала, биогенных элементов и других компонентов экосистемы. В области градиентов физических и химических характеристик формируются различные экологические ниши планктонных микроорганизмов, что приводит к формированию устойчивых неоднородностей вертикального распределения различных видов бактерио-, фито- и протозоопланктона. Для адекватного моделирования планктонных популяций в глубоких водоемах необходим расчет сезонных динамик вертикальных распределений физико-химических характеристик воды, таких как температура, содержание солей, плотность в зависимости от метеорологических условий. Кроме того, в водоемах умеренной зоны необходимо учитывать процессы образования и таяния льда в зависимости от метеоусловий.
В отчетном году выполнена модификация одномерной вертикальной модели, описывающей годовую динамику вертикальных распределений температуры и солености водной толщи с учетом процессов образования и таяния льда, а также верификация данной модели по натурным данным.
По разработанной компьютерной программе выполнена серия численных расчетов температуры, солености и плотности воды в озере Шира. В качестве начальных данных были взяты вертикальные распределения температуры и солености в глубоководной зоне озера, измеренные в конце мая. Использовались реальные метеоданные с ближайшей метеостанции. Измеренные профили солености для зим 2003 и 2004 гг. существенно различались, а именно -»ступенька» солености в 2003 г. была на 4 м глубже, чем в 2004 г. (15.3 м и 11.3 м соответственно). Аналогичная картина была получена и в модельных расчетах. Значительные различия между зимними распределениями разных лет могут объясняться лишь различиями метеорологических условий в осенний и зимний периоды.
Согласно натурным данным заглубления термоклина, халоклина и пикноклина для озера Шира практически совпадают и зависят от метеоданных и периода года. Из натурных и расчетных данных следует, что в озере Шира положение редокс-зоны совпадает со «ступенькой» плотности для осеннего и зимнего сезонов. Редокс-зона — это граница раздела слоев, насыщенных кислородом и сероводородом. Летом и весной редокс-зона находится существенно ниже пикноклина. Глубина расположения редокс-зоны является важной характеристкой стратифицированного водоема. В зависимости от того, сколько света проникает в редокс-зону, определяется видовой состав бактериального сообщества, формирующегося в этой зоне. В зоне перехода от аэробных слоев водной толщи к анаэробным (редокс-зона) обычно наблюдается повышенная активность планктонных сообществ.
Разработанная компьютерная модель позволяет прогнозировать динамику вертикальных распределений температуры, солености, плотности воды и при необходимости других компонентов экосистемы в зависимости от метеоданных.
Основные публикации:
- Белолипецкий П. В., Белолипецкий В. М., Генова С. Н.
Численное моделирование годового режима вертикальной стратификации соленого озера Шира // Материалы Национальной конф. «Математическое моделирование в экологии». — Пущино: ИФХиБПП РАН. — 2009. — С. 34-35. - Компаниец Л. А., Якубайлик Т. В., Питальская О. С.
Аналитическое решение одной модели ветрового движения вязкой жидкости // Вычислительные технологии. — 2009. — Т. 14. — № 4. — С. 46-56.
(Отдел вычислительных моделей в гидрофизике)
| К началу | |
Проект № 116 «Антропогенные риски угледобывающих и нефтегазодобывающих территорий Сибири»
Координатор проекта: д.т.н., профессор В. В. Москвичев
Блок ИВМ СО РАН «Разработка моделей и методов оценки перманентных и аварийных антропогенных рисков»
Ответственные исполнители от ИВМ СО РАН: д.т.н., профессор А. М. Лепихин, д.т.н., профессор К. В. Симонов
Выполнены исследования антропогенных опасностей, возникающих при разработке нефтегазовых месторождений Сибири. Рассмотрен технологический комплекс оборудования, используемый при разработке и освоении месторождений, включающий: буровые установки, насосное оборудование, емкости и резервуары, промысловые трубопроводы и магистральные трубопроводы. Выделены характерные источники и факторы антропогенного риска. Представлены статистические оценки вероятностей аварий указанного оборудования в природно-климатических условиях Сибири.
С учетом выделенных источников опасности разработаны модели оценки рисков штатных технологических воздействий на окружающую среду и аварийных рисков, возникающих при отказах оборудования нефтегазовых месторождений. Риски технологических воздействий рассматриваются как перманентные, постоянно действующие. Аварийные риски рассматриваются как локальные во времени и пространстве события. Разработаны обобщенные «трендовые» и «экстремальные» модели риска. В трендовых моделях анализируются процессы деградации металла и постепенного накопления повреждений, приводящие к аварийным состояниям оборудовании технологического комплекса. В экстремальных моделях рассматриваются эффекты редких запроектных воздействий, приводящих к катастрофическим отказам оборудования с утечками опасных веществ. Сформулированы обобщенные схемы оценки риска аварий на объектах газо- и нефтедобычи (буровые установки и объекты обустройства скважин), промысловых и магистральных трубопроводах и резервуарных парках с учетом природно-климатических условий Сибири и Крайнего Севера.
Объектом исследования выступают проекты освоения природных ресурсов на территории Красноярского края для оценки и прогноз эколого-экономических последствий реализации данных проектов. В рамках моделирования исходных данных разработана ГИС-модель для комплексного анализа эколого-социальных последствий развития промышленных узлов Красноярского края. Проведены экспериментальные расчеты на примере оценки эколого-социальных последствий развития Богучанско-Кодинского промышленного узла.
Выполнено исследование по оценке состояния природной среды и ожидаемого воздействия на нее объектов нефтегазового комплекса в проблеме территориального планирования Красноярского края с целью минимизации эколого-экономических ущербов на рассматриваемых территориях. Построены схемы районирования территорий освоения нефтегазовых ресурсов (Ванкор, Нижнее Приангарье) по уровню допустимой антропогенной нагрузки на природную среду.
Основные публикации:
- Лепихин А. М.
Комплексные показатели безопасности территорий // Проблемы безопасности и чрезвычайных ситуаций. — 2008. — № 5. — С.93-98. - Москвичев В. В.
Исследование проблем природно-техногенной безопасности регионов Сибири // Материалы III научн.-практ. конф. «Безопасность регионов — основа устойчивого развития». — Иркутск: ИрГУПС. — 2009. — Т. 1. — С. 54-60. - Москвичев В. В., Перетокин С. А., Сибгатулин В. Г.
Геодинамические риски и безопасность промышленных объектов // Тр. III Всерос. конф. «Безопасность и живучесть технических систем». — Красноярск: ИВМ СО РАН. — 2009. — С. 45-46. - Нарбекова Т. Н., Крушенко Г. Г.
Выявление техногенных образований металлургического производства, метод их учета и извлечения цветных металлов // Цветные металлы. — 2009. — № 5. — С. 90-93. - Nicheporchuk V. V., Lepikhin A. M., Moskvichev V. V. Simonov K. V.
Investigation of ecological danger for territories of Siberia // J. Ecology and Safety. — Burgas, Bulgaria. -2009. — Vol .3. — Part 2. — Р. 104–122 . - Nicheporchuk V. V., Lepikhin A. M., Moskvichev V. V. Simonov K. V.
Estimation method of risk parameters for atmosphere pollution of Krasnoyarsk region // Int. Conf. on Computationel information Technologies for Environmental Sciences «CITES-2009». — Krasnoyarsk, 2009. — Р. 49. - Сибгатулин В. Г., Суховольский В. Г., Перетокин С. А., Симонов К. В., Краснораменская Т. Г., Нестеренко Е. В., Кобалинский М. В.
Оценка состояния природной среды и ожидаемого воздействия на нее объектов нефтегазового комплекса Красноярского края // Сб. материалов междунар. конф. «Ресурсная экономика, изменение климата и рациональное природопользования — 2009». — Красноярск: СФУ. — 2009. — С. 410–418 . - Шишацкий Н. Г., Брюханова Е. А., Нестеренко Е. В., Коровин А. Л., Даничев А. А., Перетокин С. А., Сибгатулин В. Г., Симонов К. В.
Оценка эколого-социальных последствий освоения природных ресурсов Красноярского края на основе ГИС-моделирования // Материалы всерос. конф. «Математическое моделирования и вычислительно-информационные технологии в междисциплинарных научных исследованиях». — Иркутск: ИДСУ СО РАН. — 2009. — С. 87.
(Отдел вычислительных моделей в гидрофизике)
| К началу | |