| ИВМ СО РАН | Поиск |
| Отчеты ИВМ СО РАН |
Отчет ИВМ СО РАН за 2009 год
Интеграционные, экспедиционные проекты, гранты СО РАН
- Заказные интеграционные проекты
- Междисциплинарные интеграционные проекты
- Проекты, выполняемые совместно со сторонними научными организациями
- Проект № 89 «Эффективные вычислительные методы на последовательности сеток для решения задач математической физики»
- Проект № 103 «Законы сохранения, инварианты, точные и приближенные решения для уравнений гидродинамического типа и интегральных уравнений»
- Проект № 116 «Моделирование, оптимизация и устойчивость конвективных течений»
- Экспедиционные проекты
- Целевые программы СО РАН
Проекты, выполняемые совместно со сторонними научными организациями
Проект № 89 «Эффективные вычислительные методы на последовательности сеток для решения задач математической физики»
Координаторы проекта: член-корреспондент РАН В. В. Шайдуров
Ответственный исполнитель от ИВМ СО РАН: член-корреспондент РАН В. В. Шайдуров
1. В рамках проекта проводятся исследования сходимости многосеточных методов для квадратичных конечных элементов. Обоснована сходимость полного многосеточного метода на основе симметричного V-цикла для решения сеточной задачи, полученной дискретизацией эллиптического уравнения второго порядка с помощью квадратичных элементов на треугольниках. Доказана экономичность этого алгоритма, состоящая в линейной зависимости числа арифметических операций от количества неизвестных для определения приближенного решения с точностью, совпадающей по порядку с погрешностью аппроксимации. Полученная скорость сходимости оказалась выше, чем для линейных конечных элементов, несмотря на достижение более высокого порядка точности.
Исследовалась сходимость многосеточных итерационных методов для решения сеточной задачи, полученной дискретизацией эллиптического уравнения второго порядка с помощью кусочно-линейных элементов на треугольниках с использованием численного интегрирования. Обычно сходимость многосеточных методов обосновывается в предположении, что элементы матрицы и вектора правой части системы уравнений метода конечных элементов вычислены точно. Однако на практике они, как правило, вычисляются с использованием квадратурных формул. Рассмотрены полный многосеточный метод на основе W-цикла и каскадный алгоритм, представляющий собой наиболее простую версию многосеточных методов. Предложен способ построения дискретных задач на более грубых сетках. Доказано, что для обоих алгоритмов число арифметических операций, приходящихся на одно неизвестное, для определения приближенного решения с точностью, совпадающей по порядку с погрешностью дискретной задачи с учетом численного интегрирования, не зависит от числа неизвестных и количества сеток.
2. Подготовлена первая часть рукописи учебного пособия по многосеточным методам.
Цель данного пособия — в доступной форме изложить основные принципы многосеточных методов. Для этого общая теория рассматривается в приложении к решению модельной задачи. Теоретические результаты иллюстрируются численными примерами.
Рукопись пособия в настоящее время состоит из 5 глав.
В главе 1 содержатся сведения из линейной алгебры, функционального анализа и теории итерационных методов, которые используются при дальнейшем изложении материала. Особое внимание уделено обсуждению итерационных методов, которые используются в качестве базовых итераций в различных версиях многосеточного метода (различные версии метода простых итераций со специальными параметрами для ускорения сходимости, трехслойный полуитерационный метод, устойчивый к погрешностям округлений, метод сопряженных градиентов).
В главе 2 излагается двухсеточный метод для простейшей модельной задачи — дискретного аналога одномерного уравнения диффузии, полученного с помощью метода конечных элементов. Такой подход позволяет максимально просто изложить основные идеи многосеточного метода, не отвлекаясь на дополнительные трудности, возникающие в более общем случае. На примере метода Якоби проиллюстрировано сглаживающее свойство итерационных методов. Обсуждается идея коррекции с грубой сетки. Описано построение операторов интерполяции и проектирования для одномерной задачи. Формулируется двухсеточный алгоритм и доказывается его сходимость для модельной задачи. Для наглядности изложение материала сопровождается численными примерами, результаты расчетов представлены в виде графиков.
Глава 3 посвящена классическому многосеточному методу. Для системы линейных алгебраических уравнений сформулированы алгоритмы V- и W-цикла и полный многосеточный алгоритм. Обсуждаются различные варианты V- и W-цикла в зависимости от количества пред- и постсглаживающих итераций. Обосновываются соотношения, при помощи которых матрица итераций многосеточного метода выражается через матрицу итераций двухсеточного метода. Рассматривается сходимость W-цикла. Доказывается, что достаточным условием сходимости W-цикла является сходимость двухсеточного метода. Для двухсеточного метода, в свою очередь, достаточным условием сходимости является выполнение свойства сглаживания и свойства аппроксимации. Таким образом, доказательство сходимости W- цикла для конкретной задачи сводится к доказательству свойства сглаживания и свойства аппроксимации. Далее доказывается сходимость V-цикла для системы уравнений с симметричной и положительно определенной матрицей в предположении, что выполнены свойство сглаживания и свойство аппроксимации в соответствующей формулировке. Рассматривается вопрос о влиянии выбора сглаживающих итераций на скорость сходимости многосеточного метода.
В главе 4 обосновывается сходимость многосеточного метода для модельной задачи. Для уравнения Пуассона на квадрате строится система уравнений метода конечных элементов с использованием кусочно-линейных элементов на треугольниках. Определяются операторы интерполяции и проектирования для двумерного случая. Доказательство сходимости многосеточного метода опирается на результаты главы 3. Далее рассматривается полный многосеточный алгоритм для модельной задачи и доказывается, что он позволяет получить приближенное решение системы уравнений с точностью, сопоставимой с погрешностью дискретизации, с оптимальной оценкой числа арифметических операций. Приводятся результаты численных экспериментов, которые иллюстрируют теоретические оценки. Приводятся результаты расчетов для двух версий многосеточного метода — итерационного метода с использованием V-цикла в качестве итерации и полного многосеточного метода также с использованием V-цикла. Даются рекомендации по выбору числа сглаживающих итераций в V-цикле и числа V-циклов во внешнем итерационном методе.
В главе 5 представлен каскадный алгоритм, который является простейшей версией многосеточных методов. Изложение начинается с формулировки каскадного алгоритма для системы уравнений с симметричной и положительно определенной матрицей. В качестве сглаживающих итераций рассматриваются метод сопряженных градиентов, метод простых итераций со специальными параметрами и трехслойный полуитерационный метод. Исследование сходимости каскадного алгоритма, как и в случае V- и W-цикла, разбито на два основных этапа. Вначале обосновывается оценка погрешности каскадного алгоритма в предположении, что выполняется критерий сходимости. Затем проверяется справедливость критерия сходимости для конкретной задачи. Данный подход проиллюстрирован на примере модельной задачи — дискретного аналога уравнения Пуассона. Обсуждается способ выбора числа сглаживающих итераций на разных сетках, позволяющий достичь оптимальной вычислительной сложности в каскадном алгоритме, т.е. при конечном числе арифметических операций, приходящихся на одно неизвестное, получить погрешность того же порядка малости, что и погрешность дискретизации. Отдельно рассматривается вопрос о выборе сглаживающих итераций, поскольку этот выбор имеет решающее значение для оптимальности алгоритма. Как и в предыдущей главе, приведены результаты численных экспериментов, позволяющие дать рекомендации по выбору параметров алгоритма. В данном случае это число сглаживающих итераций на самой мелкой сетке.
3. В текущем году часть работы была посвящена построению и использованию математических моделей, описывающих с приемлемой точностью сложные физические процессы. Одной из таких моделей являются уравнения Навье-Стокса для описания сферической модели геодинамики. Обычно эти уравнения используются для описания динамики вязкого теплопроводного газа. Здесь же на их основе предложена компьютерная модель, позволяющая рассмотреть геодинамические процессы расширения, сжатия, разогревания и охлаждения Земли на геологических участках времени. Динамика геосфер исследуется в рамках модели вязкой теплопроводной сжимаемой среды, когда плотность и вязкость среды меняются во времени и пространстве. Настоящая модель позволяет рассмотреть не только кору и мантию Земли, но и её внутреннюю структуру, включая твердое и жидкое ядро.
Исследования направлены на разработку математической модели, позволяющей адаптировать данные о структуре Земли к уравнениям Навье-Стокса с помощью уравнения состояния, плотности, динамической вязкости, внутренней энергии и высоких температур. Рассматривается сферически-симметричное течение такой вязкой теплопроводной среды с учетом гравитационных сил.
4. Другой математической моделью являются уравнения мелкой воды. В последние десятилетия они все шире используются для описания течения и разлива в реках, а также гравитационных волн и цунами в морях и океанах. Один из разделов посвящен изложению одной из модификаций уравнений для описания целого комплекса явлений в речной системе: учет талых и дождевых вод, инфильтрации воды в почву и испарение, учет сброса и регулирования расхода воды на гидроэлектростанциях. Причем за счет модификации используемых уравнений они описывают весь комплекс перечисленных явлений на всей площади водосбора. В качестве отправной модели взяты уравнения Навье-Стокса для вязкой несжимаемой жидкости. Далее путем осреднения по высоте из них получаются уравнения мелкой воды, которые и служат базисом математической модели. В отличие от развитых одномерных моделей (уравнения Сен-Венана, кинематической волны и др.), эта модель более тщательно учитывает рельеф русла и поверхности водосбора и водостока, что особенно важно для прогноза половодья. Такие более сложные физико-математические модели применяются довольно редко ввиду необеспеченности эмпирическими данными. Но развитие современных средств наблюдений, в том числе космической съемки, и использование детальных геоинформационных данных рельефа дают все больше оснований для использования таких моделей.
Другая модификация уравнений мелкой воды в представленном отчете использована для описания гравитационных волн и цунами в морских акваториях.
Численное моделирование поверхностных волн в больших акваториях проводилось с учетом сферичности Земли и ускорения Кориолиса на основе уравнений мелкой воды. Ранее авторами для этой же задачи построен метод конечных элементов, для которого получены необходимые априорные оценки. Тогда же проведены численные эксперименты на одном процессоре для модельных задач.
Здесь же численные эксперименты на высокопроизводительных многопроцессорных вычислительных системах проводились на модельной прямоугольной сетке. Для реализации параллелизма по данным были разработаны алгоритмы декомпозиции вычислительной области с триангуляцией для модельных задач в прямоугольнике на сфере. Приведены сравнительные результаты ускорения вычислений в зависимости от количества процессов, способа реализации коммуникаций (блокирующие, неблокирующие передачи), способа декомпозиции вычислительной области, архитектуры суперЭВМ.
5. Разработка программных комплексов для проведения крупномасштабных вычислительных экспериментов на параллельных вычислительных системах представляет собой сложную в теоретическом и практическом плане задачу — это многоэтапный технологический процесс, включающий в себя исследование дифференциальной задачи и численного метода решения, выбор модели программы, ее декомпозицию на параллельные процессы, анализ производительности и организацию вычислительного эксперимента. Очевидно, что при разработке параллельных программ необходимо применять методы, обеспечивающие эффективное использование предоставляемых вычислительных ресурсов. Однако разнообразие архитектур параллельных вычислительных систем ведет к тому, что в настоящее время не существует языка, позволяющего создавать программы, легко и эффективно переносимые с одной архитектуры на другую.
В силу этих причин необходима разработка новых учебных курсов магистерских программ «Вычислительная математика» и «Математическое и компьютерное моделирование» — годового курса «Параллельное программирование» и полугодового курса «Особенности разработки параллельных приложений». На основе собственного опыта нескольких лет практической работы и анализа научной и учебно-методической литературы Е. Д. Кареповой разрабатывается программа двух курсов для магистерских программ, а также учебное пособие «Основы параллельного программирования».
В более широком смысле, применение вычислительной техники для системы обучения многими специалистами оценивается как весьма перспективное направление. Концепция массового образования и равных возможностей требует разработки таких механизмов обучения, которые могут быть эффективно применены не только в системе классического (аудиторного) образования, но и при самостоятельном (дистанционном) обучении. В связи с этим возникают задачи составления эффективно работающих электронных учебных курсов и разработки соответствующего программного обеспечения, подкрепленных новыми методологическими образовательными концепциями и государственными стандартами.
Этим задачам была посвящена работа, где целью рекомендованного процесса индивидуализации является оптимизация траектории представления учебного материала относительно требований обучения и информации о текущем уровне знаний пользователя. Для этого требуется иметь не только качественный учебный материал, но и знать цели обучаемого по отношению к выбранной дисциплине, а также эффективные алгоритмы индивидуализации учебного и контрольного материалов.
6. И наконец, в сентябре этого года проведена Китайско-Российская научная конференция «Эффективные вычислительные методы для решения задач математической физики» с 18 по 25.09.2009 г. в г. Пекине. На конференции в рамках интеграционного проекта СФУ — Институт вычислительного моделирования СО РАН — Институт вычислительной математики и научных-инженерных расчетов КАН российскими и китайскими участниками были сделаны доклады (российскими участниками — четыре доклада), в которых отражены направления научных исследований и основные результаты в области прикладной математики. Кроме того, состоялась дискуссия, где обсуждались возможные направления совместных исследований.
Основные публикации:
- Gileva L. V., Shaidurov V. V.
Convergence of a full multigrid algorithm for quadratic finite elements in a domain with a curvelinear boundary // Rus. Journ. of Num. Anal. and Math. Model. — 2009. — Vol. 24, № 5. — P. 425–438 . - Гилева Л. В.
Многосеточные итерационные алгоритмы в методе конечных элементов с учетом численного интегрирования // Вычислительные технологии. — 2009. — Т. 14. — № 1. — С. 34-51. - Карепова Е. Д., Шайдуров В. В., Вдовенко М. С.
Параллельные реализации метода конечных элементов для краевой задачи для уравнений мелкой воды // Вестник ЮУрГУ. Серия «Математическое моделирование и программирование». — 2009. — Вып. 3. — № 17 (150). — С. 73-85. - Карепова Е. Д.
Численное моделирование поверхностных волн в больших акваториях // Материалы семинара ИВМ СО РАН «Проблемы математического и численного моделирования». Вычислительные технологии. — 2009. — Т. 14. — № 1. — С. 28-29. - Карепова Е. Д., Шайдуров В. В.
Параллельная реализация МКЭ для начально-краевой задачи мелкой воды // Вычислительные технологии. — 2009. — Т.14. — № 6. — С. 45-57. - Вяткин А. В., Шайдуров В. В., Щепановская Г. И.
Численное сферически-симметричное моделирование глубинной геодинамики // Сибирский журнал индустриальной математики. — 2009. — Т. 2. — № 1(37). — С. 40-48. - Vyatkin A. V., Shaidurov V. V., Shchepanovskaya G. I.
The numerical spherically symmetric modeling of deep-seated geodynamics // Numerical Analysis and Its Applications. — Berlin, Heidelberg: Springer-Verlag. — LNCS 5434. — 2009. — P. 128–138 . - Шайдуров В. В., Щепановская Г. И., Якубович М. В.
Численное моделирование переноса массы (пространственный случай) // Материалы ХIII Междунар. научн. конф. «Решетневские чтения». — Красноярск: СибГАУ. — 2009. — С. 320.
(Отдел вычислительной математики)
| К началу | |
Проект № 103 «Законы сохранения, инварианты, точные и приближенные решения для уравнений гидродинамического типа и интегральных уравнений»
Координаторы проекта: д.ф.-м.н., профессор С. Б. Медведев, д.ф.-м.н., профессор М. Ю. Филимонов, д.ф.-м.н., профессор К. В. Кошель
Ответственный исполнитель от ИВМ СО РАН: д. ф.-м..н., профессор О. В. Капцов
Построены примеры подмоделей уравнений Эйлера течения идеальной несжимаемой жидкости, обладающих тем свойством, что допускаемая группа, действующая на уравнениях подмодели, имеет функциональный произвол. Приведены примеры точных решений найденных подмоделей.
Найдена полная группа преобразований, допускаемая полуэмпирической трехмерной моделью турбулентности в приближении дальнего турбулентного следа. Искомыми величинами в данной модели являются кинетическая энергия турбулентности, скорость диссипации кинетической энергии турбулентности, осредненный дефект плотности, дисперсия флуктуаций плотности. На основе полученных автомодельных представлений и с помощью метода B-определяющих уравнений рассматриваемая модель редуцирована к системе обыкновенных дифференциальных уравнений. Построены численные решения, удовлетворяющие естественным краевым условиям. Полученные решения согласуются с экспериментальными данными на качественном и количественном уровнях.
Основные публикации:
- Шанько Ю. В.
О подмоделях с широкой группой симметрий // Тез. всерос. конф. «Новые математические модели механики сплошных сред: построение и изучение». — Новосибирск. — 2009. — С. 158–159 . - Капцов О. В., Шмидт А. В.
Неавтомодельные решения задачи об эволюции зоны турбулентного смешения в пассивно стратифицированной среде // Тез. междунар. конф. «Потоки и структуры в жидкостях: физика геосфер». — Москва. — 2009. — C. 114. - Капцов О. В., Шмидт А. В.
Неавтомодельные решения трехмерной k-epsilon модели // Тез. междунар. конф. «Вычислительная математика, дифференциальные уравнения, информационные технологии». — Улан-Удэ. — 2009. — C. 271–277 .
(Отдел вычислительных моделей в гидрофизике)
| К началу | |
Проект № 116 «Моделирование, оптимизация и устойчивость конвективных течений»
Координатор проекта: член-корреспондент РАН В. В. Пухначёв
Блок ИВМ СО РАН «Исследование устойчивости состояний равновесия и стационарных течений в неклассических моделях конвекции»
Ответственный исполнитель от ИВМ СО РАН: д.ф.-м.н., профессор В. К. Андреев
1. Рассмотрены плоские и пространственные возмущения стационарного конвективного двухслойного течения вязкой термокапиллярной жидкости в плоском наклонном канале. Гладкая поверхность Γ делит область течения на две подобласти Ω1 = {|x| < ∞, −h2 < y < 0} и Ω2 = {|x| < ∞, 0 < y < h1}. На стенках канала y = −h2, y = h1 заданы условия прилипания и линейный закон изменения температуры θj = Tjx + θj0, j = 1,2. В каждой из областей справедлива система уравнений Обербека-Буссинеска, в которой вектор g имеет координаты g = (g sin φ, −g cos φ), здесь g — ускорение свободного падения, φ — угол отклонения от горизонтали.
Для всех классов точных решений построены нейтральные кривые (рис. 41, 42).
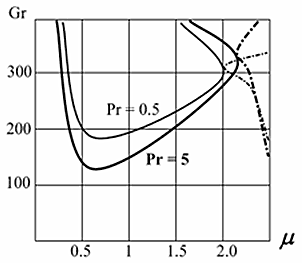
Рис. 41. Нейтральные кривые
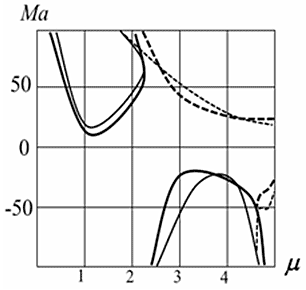
Рис. 42. Нейтральные кривые
На рис. 41 приведены нейтральные кривые Gr(μ) для течений в наклонном канале с нулевым продольным градиентом температуры. Сплошными линиями обозначены кривые монотонной неустойчивости, штриховыми — колебательной. Области неустойчивости расположены внутри кривых. На рис. 42 изображены нейтральные кривые Ma(μ) для течений в наклонном канале. Тонкими линиями обозначены кривые для течения в наклонном канале, когда стенки канала нагреваются в направлении течения, жирными — для случая, когда охлаждаются.
Изучено влияние угла наклона системы на характер неустойчивости (рис. 43). В случае горизонтальной ориентации слоя имеет место только монотонная неустойчивость, а при любом отклонении системы имеем и колебательные возмущения. При изменении угла наклона имеет место смена форм неустойчивости: в случае малых углов наиболее опасными являются плоские возмущения (как и в случае изотермических течений), а при больших углах φ (близких к 90°) — пространственные возмущения.
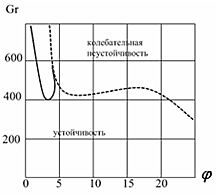
Рис. 43. Нейтральные кривые Gr(φ)
2. Для случая недеформируемых границ раздела было найдено состояние термодиффузионного равновесия. Определены области устойчивости этого состояния по отношению к малым возмущениям системы, а также изучено влияние термоконцентрационных эффектов на поверхности раздела бинарных смесей. Показано, что с ростом термодиффузионных эффектов на поверхности раздела жидкость-жидкость область устойчивости смещается в сторону длинных волн, а рост числа Марангони приводит к понижению длинноволновой устойчивости. Усиление термокапиллярных явлений на свободной поверхности уменьшает область длинноволновой устойчивости состояния термодиффузионного равновесия. Общая спектральная задача относительно комплексного декремента решена численно методом ортогонализации, адаптированным для задач с граничными условиями на твердой стенке, свободной границе и поверхности раздела. Определены области длинноволновой устойчивости для некоторой системы бинарных смесей. Обнаружено, что при фиксированных числах Марангони в случае увеличения числа Соре на поверхности раздела порог устойчивости для длинноволновых возмущений понижается.
3. Исследована устойчивость состояния термодиффузионного равновесия двухслойной системы бинарных смесей с общей поверхностью раздела при условии деформации поверхности раздела. Построены нейтральные кривые и определены области длинноволновой устойчивости для некоторой системы бинарных смесей.
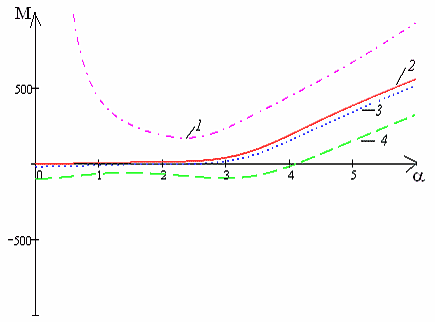
Рис. 44. Нейтральные кривые для системы бинарных смесей с общей деформируемой поверхностью раздела, область устойчивости находится ниже кривых. Кривая 1 соответствует системе с недеформируемой поверхностью раздела жидкостей, кривая 2 — для Sr = −1, 3 — Sr = −10, 4 — Sr = −100
Показано, как изменяются области устойчивости при варьировании безразмерных параметров задачи. Например, рост числа Соре (т. е. усиление термоконцентрационных эффектов) на поверхности раздела смесей приводит к росту критического значения числа Марангони, при котором происходит смена устойчивости. Кроме того, деформируемость поверхности раздела приводит к понижению критического значения числа Марангони и уменьшению области длинноволновой устойчивости.
Основные публикации:
- Андреев В. К., Собачкина Н. Л.
Свойства решений начально-краевой задачи, возникающей при движении бинарной смеси в цилиндрической трубе // Препринт № 2. — Красноярск: ИВМ СО РАН. — 2009. — 40 с. - Бекежанова В. Б.
О конвективной неустойчивости двухслойного течения жидкости на наклонной плоскости // Тез. докл. всерос. конф. «Новые математические модели механики сплошных сред: построение и изучение». — Новосибирск: ИГиЛ СО РАН. — 2009. — С. 32-33. - Бекежанова В. Б.
Задача об устойчивости стационарного течения в системе горизонтальных слоёв несмешивающихся жидкостей // Тез. докл. всерос. конф. «Успехи механики сплошных сред». — Владивосток: Дальнаука. — 2009. — С. 56. - Bekezhanova V. B.
Instability of stationary two-layer fluid flow with longitudinal gradient of temperature // Vodic konferencije «Matimatickel i informacione tehnologije (MIT — 2009)». — Kosovska Mitrovica: Univerzitet u Pristini. — 2009. — P. 57. - Ефимова М. В.
Об устойчивости равновесного состояния двухслойной системы бинарных смесей со свободной границей // Тез. докл. всерос. конф. «Новые математические модели механики сплошных сред: построение и изучение». — Новосибирск: ИГиЛ СО РАН. — 2009. — С. 63. - Ефимова М. В.
Возникновение конвекции в двухслойной системе с деформируемыми поверхностями раздела // Тез. докл. всерос. конф. «Математика в приложениях». — Новосибирск: ИМ СО РАН. — 2009. — С. 114–115 . - Ефимова М. В.
Неустойчивость равновесного состояния двух бинарных смесей с общей поверхностью раздела и одной свободной границей // J. of Siberian Federal University. Mathematics and Physics. — 2009. — № 2(2). — P. 158–166 .
(Отдел дифференциальных уравнений механики)
| К началу | |