| ИВМ СО РАН | Поиск |
| Отчеты ИВМ СО РАН |
Отчет ИВМ СО РАН за 2011 год
Программы фундаментальных исследований Сибирского отделения РАН
- III.19. Общая механика, динамика космических тел, транспортных средств и управляемых аппаратов, биомеханика, механика жидкости, газа и плазмы, неидеальных и многофазных сред, а также механика горения, детонации и взрыва
- IV.29. Системы автоматизации, CALS-технологии, математические модели и методы исследования сложных управляющих систем и процессов
- IV.31. Проблемы создания глобальных и интегрированных информационно-телекоммуникационных систем и сетей. Развитие технологий GRID
- VI.32. Архитектура, системные решения, программное обеспечение и информационная безопасность информационно-вычислительных комплексов и сетей новых поколений. Системное программирование
VI.32. Архитектура, системные решения, программное обеспечение и информационная безопасность информационно-вычислительных комплексов и сетей новых поколений. Системное программирование
Программа IV.32.1. Архитектура, информационная безопасность, системные решения и программное обеспечение информационно-вычислительных систем новых поколений
Координаторы программы: член-корреспондент РАН В. Г. Хорошевский, член-корреспондент РАН В. В. Шайдуров
Проект IV.32.1.4. «Анализ сложных математических моделей на суперкомпьютерах с параллельной архитектурой»№ гос. регистрации 01201056402
Научный руководитель проекта: д.ф.-м.н., проф. В. М. Садовский
Блок 1. Техническое сопровождение исследований (С. В. Исаев, А. В. Малышев).
Выполнен запланированный объем работ по обеспечению работоспособности высокопроизводительных вычислительных ресурсов ИВМ СО РАН. В настоящее время в Институте имеется два компьютера кластерной архитектуры: МВС-1000/16 с пиковой производительностью 14,0 Гфлоп и МВС-1000/146 с производительностью по Linpack 450 Гфлоп и пиковой производительностью 680 Гфлоп. Кроме того, на площадях ИВМ СО РАН установлен и находится в совместном использовании кластер IBM System x3755 Сибирского федерального университета с производительностью по LinPack 450 Гфлоп и пиковой производительностью 1,043 Тфлоп. Организован доступ по гигабитной сети к большому кластеру СФУ, занимающему в настоящее время 31-е место в Top50 самых мощных суперкомпьютеров СНГ.
В 2011 г. ИВМ СО РАН получил грант РФФИ на развитие материально-технической базы, за счет которого приобретен высокопроизводительный вычислительный сервер Flagman RX240T8.2 на базе графических процессоров Tesla C2050, имеющий два шестиядерных процессора Intel Xeon X5670 и 8 GPU nVidia Tesla C2050. Пиковая производительность этого сервера составляет 8,24 Тфлоп при операциях с одинарной точностью и 4,12 Тфлоп при операциях с двойной точностью. В настоящее время организован телекоммуникационный доступ к этому ресурсу, осуществляется опытная эксплуатация. Также за счет гранта РФФИ в 2011 г. приобретена система хранения данных IBM System Storage DS3512 на 12 Тбайт с поддержкой протокола iSCSI. Система используется для хранения данных и результатов вычислений на высокопроизводительных компьютерных системах.
В 2011 г. проводились работы по технической поддержке и обеспечению доступа пользователей к вычислительным ресурсам. Выполнялись работы по установке и обновлению программного обеспечения, по техническому обслуживанию и администрированию кластеров.
За счет программы СуперЭВМ Сибирского отделения РАН был приобретен 48-ядерный высокопроизводительный вычислительный модуль со следующими характеристиками:
- процессоры: 4 шт. 2.20GHz AMD Opteron 6174 12-Core 6400MHz System Bus, 12x512KB L2 cache, 12MB L3 cache;
- оперативная память: 16 шт. DIMM 4096MB DDR-3 РС3-10600 ЕСС Registered;
- сетевые интерфейсы: 2 шт. IntelR 82576 Gigabit LAN Network Interface Controller w/VMDq support.
Установка этого модуля позволила в полтора раза увеличить производительность основного кластера ИВМ СО РАН. Кроме того, на средства программы приобретены два высокопроизводительных управляемых коммутатора HP E4204-44G-4SFP vl, позволяющих обеспечить высокоскоростной доступ на вторую серверную площадку ИВМ СО РАН, на которой размещается новое оборудование.
С применением суперкомпьютерных вычислений получен ряд новых научных результатов в области математического моделирования природных и технологических процессов.
Блок 2. Моделирование акустических волн в тонких прослойках слоистой среды типа горной породы (В. М. Садовский, О. В. Садовская, М. П. Варыгина).
К описанию дисперсии акустических волн в тонких прослойках слоистой среды типа горной породы применена модель наследственной теории упругости Поинтинга-Томсона, определяющие уравнения которой формулируются в терминах напряжений, деформаций и скоростей изменения напряжений и деформаций. Исследовано дисперсионное уравнение этой модели, описывающее одномерные движения с плоскими волнами. Показано, что в такой среде скорость монохроматической волны существенно растет с увеличением частоты. Получены формулы пересчета феноменологических параметров модели через характерные скорости низкочастотных и высокочастотных волн и через декремент затухания высокочастотных волн. Разработаны алгоритмы для численного решения задач о распространении волн напряжений в многослойных структурах с вязкоупругими тонкими прослойками, реология которых описывается моделями Максвелла, Кельвина-Фойхта и Поинтинга-Томсона. Подпрограммы, реализующие эти алгоритмы, включены в комплексы программ для расчета динамики блочных массивов разнородных упругих, упругопластических и сыпучих сред на многопроцессорных вычислительных системах. В расчетах одномерной задачи о распространении плоских продольных волн в слоистой среде обнаружены медленные волны маятникового типа, которые возникают в результате многократного переотражения волн от тонких прослоек.
Блок 3. Разработка эффективных методов третьего порядка точности для численного решения систем обыкновенных дифференциальных уравнений в задачах нелинейной механики и молекулярной динамики. Программная реализация методов на многопроцессорных ЭВМ (Е. А. Новиков, А. Е. Новиков, Г. В. Ващенко).
Для вычислительных систем кластерной архитектуры построены параллельные алгоритмы интегрирования переменного шага на основе явных численных методов типа Рунге-Кутты с первого по третий порядок точности. Для метода первого порядка получена оценка локальной ошибки, а для методов второго и третьего порядков оценка аналога глобальной ошибки. Построенные оценки определяются через ранее вычисленные стадии метода и не приводят к увеличению вычислительных затрат, они применяются для выбора величины шага интегрирования в зависимости от поведения решения. Дополнительно для методов второго и третьего порядков точности получена оценка максимального собственного числа матрицы Якоби исходной задачи. Данная оценка определяется степенным методом без вычисления матрицы Якоби через ранее вычисленные стадии и поэтому не приводит к существенному увеличению вычислительных затрат. Так как полученная оценка достаточно грубая, то она используется как ограничитель на рост величины шага интегрирования на участках установления решения. Явные методы с контролем точности и устойчивости можно применять для решения умеренно жестких задач большой размерности. Получены теоретические оценки эффективности и масштабируемости параллельных алгоритмов для многопроцессорных вычислительных систем с распределенной памятью. Создан комплекс параллельных программ, в состав которого включены программные реализации разработанных алгоритмов. Построены тестовые задачи, на которых проведена проверка работоспособности и эффективности созданных программ. Разработанный комплекс применен для решения задачи многостадийного синтеза вещества без ветвления и стоков, включая задачу моделирования функционирования генной сети.
Разработаны параллельные алгоритмы на основе L-устойчивого (2,1)-метода второго порядка с постоянным и переменным шагом интегрирования. Для контроля точности вычислений и автоматического шага интегрирования построена оценка аналога глобальной ошибки. Данная оценка определяется с применением ранее вычисленных стадий и поэтому фактически не приводит к увеличению вычислительных затрат. Получены теоретические оценки эффективности и масштабируемости для вычислительных систем кластерной архитектуры. Проведена проверка работоспособности и эффективности созданных программ на ряде тестовых примеров. Разработан эффективный L-устойчивый метод третьего порядка точности для численного решения систем обыкновенных дифференциальных уравнений в задачах нелинейной механики и молекулярной динамики. Анализ результатов расчетов показал, что коммуникационные затраты составляют значительную часть общего времени решения. Увеличение числа процессоров не всегда приводит к уменьшению временных затрат.
Созданные программы на основе L-устойчивых методов использовались для решения задачи проникновения помеченных радиоактивной меткой антител в пораженную опухолью ткань живого организма. Решение приведено на рис. III.23.
В основу алгоритмов для вычисления гарантированных границ множеств решений обыкновенных дифференциальных уравнений с неточно заданными данными, ориентированных на задачи оценки надежности и безопасности сложных систем, положены символьные формы представления решений. На разных этапах реализации метода поочередно обрабатываются числовые и символьные данные. Структуры символьных данных состоят из формальной линейной комбинации корневых помеченных деревьев, операции над которыми производятся путем вложения структур данных в ассоциативный набор данных. Для повышения скорости выполнения предложен параллельный алгоритм обработки поддеревьев с однотипными операциями. Реализован алгоритм, по которому оптимальное дерево строится по схеме сдваивания, применяемой к набору вершин. Этот набор упорядочивается по возрастанию уровней, затем список просматривается слева направо и модифицируется. При вычислении границ применяется алгоритм поиска экстремальных значений, главная идея которого состоит в параллельном выполнении итераций с периодическим обменом рекордами и перераспределением областей поиска между процессорами.
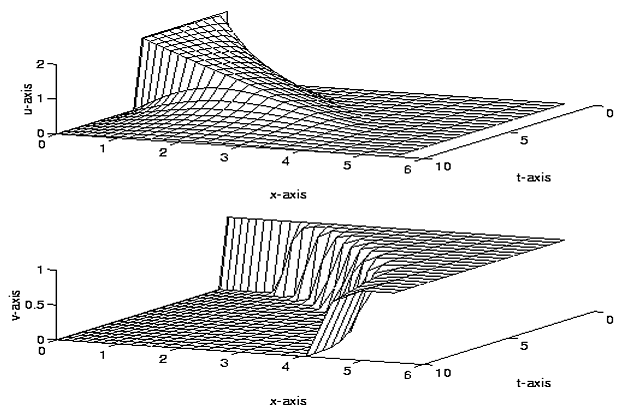
Рис. III.23. Изменение концентрации антитела с радиоактивной меткой (u) и концентрации ткани (v) в полубесконечной пластине
Блок 4. Параллельные реализации в задачах динамики взаимодействующих частиц (Л. П. Каменщиков).
В рамках блока рассматриваются методы решения с распараллеливанием при расчетах траекторий движения взаимодействующих материальных частиц, находящихся, в общем случае, также под действием некоторого внешнего силового поля. Модель сводится к системе обыкновенных дифференциальных уравнений для определения координат частиц и для их скоростей.
Интерпретация самого понятия «частица», действующих сил, интервала интегрирования и другие детали в модели зависят от конкретной области приложений. Метод частиц широко применяется при компьютерном моделировании в молекулярной биологии и химии для исследования структуры и динамики макромолекул, в механике жидкостей, газов и твердых тел, в физике плазмы и т.п. Макроскопические свойства системы определяются усреднением состояний отдельных частиц по всей системе. Преимущество метода частиц в том, что он требует значительно меньше априорных предположений о свойствах изучаемого материала, чем методы, основанные на концепции сплошной среды. Когда число частиц достаточно велико, а также для нахождения средних величин при расчетах стохастических сил, действующих на частицы, может потребоваться распараллеливание.
Решалась, в частности, задача молекулярной динамики, в которой парное взаимодействие частиц описывается известным потенциалом Ленард-Джонса. Для решения системы ОДУ можно использовать различные численные методы: Рунге-Кутты, семейство предиктор-корректор, Гира и т.д. Основные затраты машинного времени обычно уходят на расчет правой части, особенно при наличии дальнодействующих сил (гравитационных, кулоновских), поэтому желательно вычислять правую часть по возможности реже. В данной работе применяли метод Штёрмера-Верле, в котором правая часть вычисляется только один раз на каждом временном шаге, и который имеет более высокую точность по сравнению с обычным методом Эйлера, т.е. метод является компромиссом между точностью расчетов и скоростью их выполнения. Данный метод также сохраняет ряд первых интегралов исходной системы уравнений (полный импульс, полный момент импульса), что бывает важнее, чем повышенный порядок.
Для распараллеливания алгоритма применяли метод декомпозиции атомов, в котором каждый процессор на всем интервале интегрирования «отвечает» за расчет силы и решение уравнений движения только для некоторого подмножества всех атомов. Каждому процессору назначается подматрица матрицы правой части, состоящая из N/P строк матрицы, где P — число процессоров и каждый процессор вычисляет элементы своей подматрицы. Для выполнения параллельных расчетов использовали высокоуровневый подход к программированию на базе DVM-системы, разработанной в ИПМ им. М. В. Келдыша РАН. Расчеты проводились на кластере МВС-100K (1460 узлов, 11680 ядер) в МСЦ РАН. В таб. III.2 приведены время счета и коэффициент эффективности распараллеливания по DVM, определяемый как отношение Prod/(Prod+Lost), где Prod — полезное время, суммарное по всем процессорам, а Lost — суммарное время потерь, образуемое дублирование вычислений (недостаточный параллелизм), общим временем коммуникаций, простоями и т.п.
Как видно из таблицы, при числе частиц порядка 10 тысяч затраты времени можно считать приемлемыми. При больших порядках числа частиц время счета при использовании метода «декомпозиции атомов» слишком велико. Необходимо привлекать другие способы распараллеливания.
Блок 5. Определение областей практической устойчивости нелинейных систем ОДУ (А. Н. Рогалев).
Разработаны программы для исследования безопасности состояний систем, описываемых линейными обыкновенными дифференциальными уравнениями. Вычислены внешние оценки множества достижимости интегратора Брокетта, являющегося одним их первых примеров системы, для которой требуется введение нелинейного управления.
Реализованы алгоритмы, вычисляющие границы области практической устойчивости нелинейных систем обыкновенных дифференциальных уравнений. В качестве примера на рис. III.24 приведена область устойчивости системы, описывающей стабилизацию кругового движения материальной точки, управляемой реактивной силой в центральном поле. Для оценки практической устойчивости вычисляются гарантированные границы множества решений возмущенного движения.
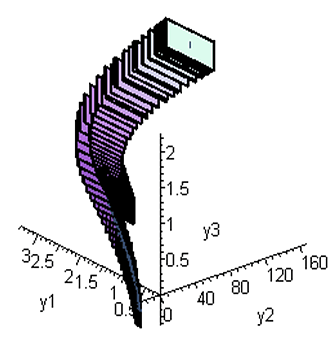
Рис. III.24. Границы области устойчивости системы, описывающей стабилизацию в поле центральной силы кругового движения материальной точки, управляемой реактивной силой
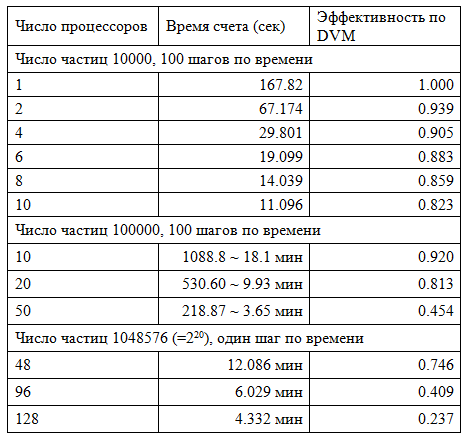
Таблица III.2. Характеристики распараллеливания
Получены оценки решений в задаче Булгакова о максимальном отклонении, принадлежащей классу задач робастной оптимизации и минимаксного контроля. В качестве примера рассмотрена задача минимизации накопленных возмущений угловых параметров корабля на прямом курсе при ограниченных по модулю ветровых возмущениях.
Блок 6. Модель построения критерия прочности линейно-армированных боропластиков при сложном температурно-силовом нагружении (С. Ф. Пятаев).
Предложена модель построения критерия прочности линейно-армированных боропластиков при сложном температурно-силовом нагружении. Модель основана на структурном подходе, при котором прочность композита определяется через анализ микронапряжений, что позволяет избежать неоднозначности, присущей феноменологическим подходам, указать область в компазитном материале, в которой зарождается начало разрушения, и предоставляет возможность дальнейшего отслеживания процесса разрушения.
Для композитной системы «эпоксидная матрица − борные волокна» в пространстве главных напряжений $<\sigma_{11}>,<\sigma_{22}>,$$<\sigma_{33}>\; $проведены численные расчеты, в которых составляющие фазы имели следующие характеристики: $E_{m} =3$ ГПа, $E_{p} =72$ ГПа; $\nu _{m} =0.3$, $\nu _{p} =0.2$; $\sigma _{m} =60$ МПа, $\sigma _{p} =3.5$ ГПа — пределы прочности матрицы и волокна соответственно. Коэффициенты линейного расширения при различных температурах имели следующие значения:
\[T_{0} =20\, ^{\circ } {\rm C} : \alpha _{m}^{0} =1.92\times 10^{-5} \; ^{\circ } {\rm C}^{-1}, \quad \alpha _{p}^{0} =0.414\times 10^{-5} \; ^{\circ } {\rm C}^{-1} ;\] \[T_{1} =180\, ^{\circ } {\rm C} : \alpha _{m}^{1} =3.54\times 10^{-5} \; ^{\circ } {\rm C}^{-1}, \quad \alpha _{p}^{1} =0.538\times 10^{-5} \; ^{\circ } {\rm C}^{-1} .\]
Из-за отсутствия дополнительных данных зависимость коэффициентов линейного расширения от температуры предполагалась линейной, а в качестве условия прочности для каждой фазы выбиралось условие Мизеза.
Расчеты при различных значениях температуры $\textit{T}$ показали, что поверхности прочности $P_{T} $ почти не изменяются по форме и размерам и близки к эллиптическому цилиндру, симметричному относительно плоскости $<\sigma _{11} >=<\sigma _{22} >$. От оси $<\sigma _{33} >$ цилиндр отклоняется примерно на 5 − 7 градусов и ограничен снизу и сверху близкими к эллипсоидам поверхностями с полуосями, много большими значений полуосей цилиндра. Часть поверхности $P_{T_{0} } $ при $T_{0} =20\, ^{\circ } {\rm C}$ ($\Delta T=0\, ^{\circ } {\rm C}$) представлена на рис. III.25(а), остальные симметричны относительно плоскости $<\sigma _{11} >=<\sigma _{22} >$ и начала системы координат (на рисунках второй индекс у $<\sigma _{ii} >$ не приводится). На рис. III.25(б) изображены сечения этой поверхности плоскостями $<\sigma _{33} >/\sigma _{m} ={\rm const}$. Кривые $\gamma _{4} -\gamma _{6} $ внутри сечений отражают вышеупомянутую эллипсоидальность ограничивающих поверхностей, а на «пике» в результате пересечения ограничивающей поверхности с цилиндром они совпадают с $\gamma _{3} $.
При изменении $\textit{T}$ поверхности $P_{T} $ возникают как результат трансляции поверхности $P_{T_{0} } $ вдоль плоскости $<\sigma _{11} >=<\sigma _{22} >$. Сечения поверхностей $P_{T} $ ($T=20\, ^{\circ } {\rm C},\; 100\, ^{\circ } {\rm C},\; 180\, ^{\circ } {\rm C}$) этой плоскостью представлены на рис. III.26, который наглядно демонстрирует перенос поверхности $P_{T_{0} } $.
Сравнение полученных расчетных значений прочности $\sigma _{com(i)} \, (i=1,3$ — нагружение композита осуществляется поперек и вдоль волокон соответственно) с экспериментальными данными при одноосных нагружениях показали их хорошее совпадение. Так, при нагружении вдоль волокон расчетный предел прочности $\sigma _{com(3)} \approx 20\sigma _{m} =1.2$ ГПа, экспериментальный — 1.6 ГПа; при нагружении поперек волокон расчетное значение $\sigma _{com(1)} \approx 0.85\sigma _{m} =51$ МПа, экспериментальное — 55 МПа. Отклонение расчетных данных от экспериментальных в сторону уменьшения объясняется тем, что построенная модель описывает начало зарождения разрушения, а экспериментальные данные отражают полное разрушение композитной системы.
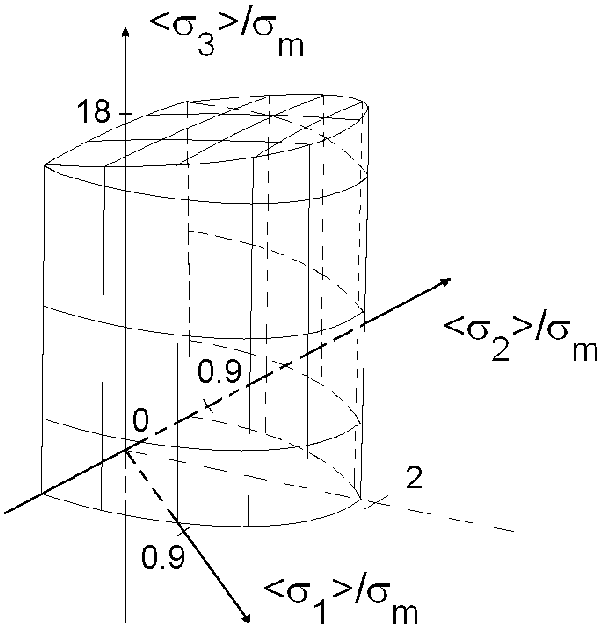
Рис III.25а. Поверхность прочности $P_{T_{0} }$ при $T_{0} =20\, ^{\circ } {\rm C}$
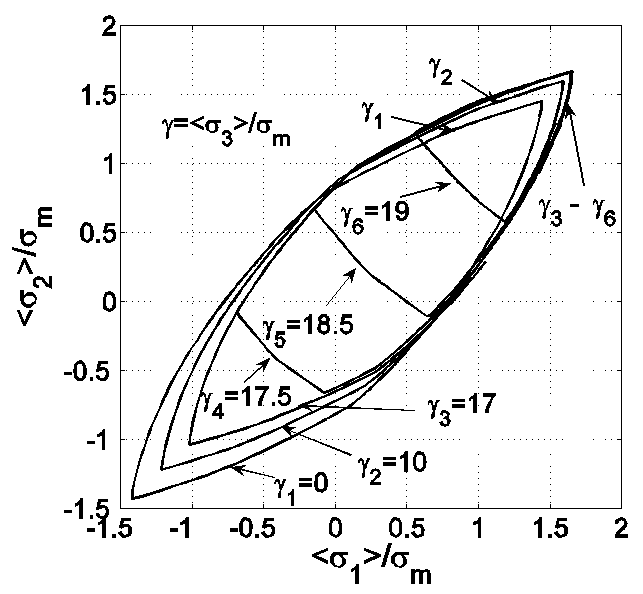
Рис III.25б. Сечения поверхности $P_{T_{0} }$ плоскостями $<\sigma _{33}>=$ const
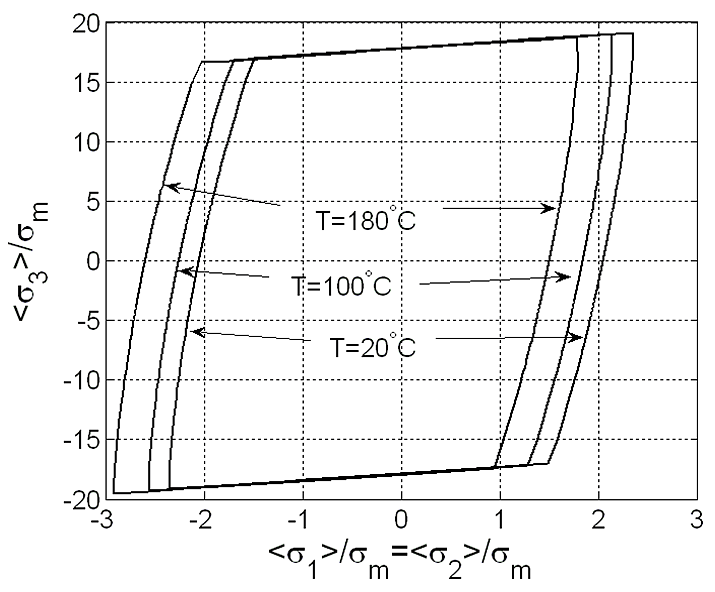
Рис. III.26. Сечения поверхностей $P_{20}, \, P_{100}, \, P_{180} $ плоскостью $<\sigma _{11}>=<\sigma _{22}>$
Блок 7. Оценка параметров сейсмической опасности (К. В. Симонов).
Исследована задача краткосрочной оценки параметров сейсмической опасности на основе анализа и интерпретации данных геомониторинга о предвестниках в процессе подготовки ожидаемого сильного землетрясения для выделенной очаговой области. Разработано алгоритмическое и программное обеспечение для сравнительного анализа данных геомониторинга очаговых зон на основе вейвлет-преобразования и корреляционного анализа, с учетом влияния глобальных геодинамических факторов, в частности, координат барицентра системы Земля — Луна. Выполнена параметризация энергетических характеристик изучаемого процесса для получения оценки времени и магнитуды ожидаемого основного события. На этой алгоритмической основе проведены расчеты по оценке искомых параметров для ряда сильнейших землетрясений, произошедших в 2006 — 2011 гг.
Основные публикации:
К блоку 2:
- Варыгина М. П., Похабова М. А., Садовская О. В., Садовский В. М.
Вычислительные алгоритмы для анализа упругих волн в блочных средах с тонкими прослойками // Вычислительные методы и программирование: новые вычислительные технологии. — 2011. — Т. 12. — С. 435–442 .
К блоку 3:
- Новиков Е. А.
Аппроксимация матрицы Якоби в (m,2)-методах решения жестких задач // ЖВМ и МФ. — 2011. — Т. 51. — № 12. — С. 2194–220 8. - Novikov E. A.
The Global Error of One-Step Solution Methods for Stiff Problems // Russian Mathematics (Iz. VUZ). — 2011. — V. 55 (6). — P. 68-75. — doi: 10.3103/S1066369X11060107. - Новиков Е. А.
Численное моделирование кольцевого модулятора (3,2)-методом решения жестких задач // Информатика и системы управления. — 2011. — № 1(27). — С. 50-61. - Новиков А. Е., Новиков Е. А.
Комбинированный алгоритм третьего порядка для решения жестких задач // Вычислительные технологии. — 2011. — Т. 16. — № 6. — С. 54-68. - Ващенко Г. В., Новиков Е. А.
Параллельная реализация явного метода Эйлера с контролем точности вычислений // Журнал СФУ. Серия: математика и физика. — 2011. — № 4(1). — С. 70-76.
К блоку 4:
- Каменщиков Л. П.
Параллельные реализации в задачах динамики взаимодействующих частиц // Расширенные тез. докл. всерос. конф. по вычислительной математике КВМ-2011. [Электронный ресурс] / Всерос. конф. — Новосибирск, Россия, 29 июня — 1 июля 2011 г. Новосибирск, ИВМиМГ СО РАН, Режим доступа: http://www.sbras.ru/ws/show_abstract.dhtml?ru+220+16194, С. 37-40, свободный. — Загл. с экрана (дата обращения: 12.08.2011). - Каменщиков Л. П.
О реализации метода частиц на параллельных ЭВМ // Современные проблемы математики, информатики и биоинформатики [Электронный ресурс] / Междунар. конф., посвященная 100-летию со дня рождения члена-корр. АН СССР А. А. Ляпунова, 11-14 октября 2011 г., Новосибирск, Россия. Режим доступа:I http://conf.nsc.ru/Lyap-100/reportview/75459 свободный. — Загл. с экрана (дата обращения 14.11.2011).
К блоку 5:
- Рогалев А. Н.
Вычисление гарантированных границ множеств достижимости управляемых систем // Автометрия. — 2011. — Т. 47. — № 3. — С. 100–112 .
К блоку 7:
- Кашкин В. Б., Симонов К. В., Григорьев А. С.
Космический мониторинг: атмосферные отклики сильных землетрясений, обнаруживаемые космическими средствами дистанционного зондирования Земли // Инженерная экология. — 2011. — № 2. — С. 38-54.
(Отделы Вычислительной математики, Вычислительной механики деформируемых сред, Служба средств телекоммуникаций и вычислительной техники)
| К началу | |