| ИВМ СО РАН | Поиск |
| Отчеты ИВМ СО РАН |
Отчет ИВМ СО РАН за 2009 год
Гранты российских научных фондов
- Гранты российских научных фондов
- Грант РФФИ №
07–01–00 006-а — «Разработка и исследование комбинированных непараметрических систем распознавания образов» - Грант РФФИ №
07–01–00 153-а — «Численное моделирование гидрофизических и гидробиологических процессов в стратифицированных водоемах» - Грант РФФИ №
07–01–00 326-а «Кубатурные формулы и их приложения к задачам геоэкологии» - Грант РФФИ №
07–01–00 489-а — «Преобразования, эквивалентность и точные решения дифференциальных уравнений с частными производными» - Грант РФФИ
07–05–00 135-а — «Математическое моделирование влияния истечения плазмы из ионосферы на формирование хвоста магнитосферы Земли» - Проект РФФИ №
08–01–00 148 — «Параллельные вычисления в задачах динамики упругопластических и сыпучих сред» - Грант РФФИ №
08–01–00 621 — «Вычислительные технологии для расчета течений несжимаемой жидкости» - Грант РФФИ №
08–05–00 137-а «Закономерности абиогенного массопереноса техногенных радионуклидов в пресноводных водоемах на примере экосистемы р. Енисей» - Грант РФФИ №
08–01–00 762 — «Конвективные течения и их устойчивость в областях с подвижными границами» - Грант РФФИ №
09–01–00 395-а — «Условия конечности в бесконечных группах» - Грант РФФИ №
09–01–06 062-г — «Организация и проведение XVII Всероссийского семинара «Нейроинформатика, ее приложения и анализ данных"" - Грант РФФИ №
09–01–06 063-г — «Организация и проведение XII Всероссийского семинара «Моделирование неравновесных систем"" - Грант РФФИ №
09–02–07 011 Издание монографии «Методы интегрирования уравнений с частными производными» - Грант РФФИ №
09–05–91 000-АНФ-а — «МГД аспекты «флэппинг» колебаний токового слоя магнитосферного хвост» - Грант РФФИ-ККФПНиНТД
09–07–98 002-р_сибирь_а — «Методология и технология создания системы управления территориальным развитием с использованием геоинформационного моделирования (на примере Нижнего Приангарья)» - Проект МК-299.2009.1 «Структуры и устойчивость конвективных течений в многокомпонентных смесях и двухфазных системах»
- Грант Фонда содействия отечественной науке по программе «Кандидаты и доктора наук РАН»
Грант РФФИ №
Руководитель: д.т.н., профессор А. В. Лапко
Разработаны методические и алгоритмические средства синтеза и анализа комбинированных систем классификации для решения многоальтернативных задач распознавания образов в условиях обучающих выборок большой размерности. Полученные результаты развиты для решения задач классификации при наличии пропусков данных в обучающих выборках. Исследованы асимптотические свойства статистических оценок показателей эффективности предложенных комбинированных систем распознавания образов. На этой основе разработаны критерии оценивания их областей компетентности в зависимости от объёма исходной информации и особенностей структуры изучаемых систем. Созданы программные средства для синтеза и анализа комбинированных систем распознавания образов в условиях обучающих выборок большой размерности.
Основные публикации:
- Лапко А. В., Лапко В. А., Егорочкин И. А.
Непараметрические оценки смеси плотностей вероятности и их применение в задаче распознавания образов // Системы управления и информационные технологии. — 2009. — Вып. 1(35). — С. 60-64. - Лапко В. А., Варочкин С. С., Егорочкин И. А.
Разработка и исследование непараметрической оценки плотности вероятности, основанной на принципе декомпозиции обучающей выборки по её объёму // Вестник СибГАУ. — 2009. — Вып. 1(22). — Ч. 1. — С. 45-49. - Лапко А. В., Лапко В. А., Саренков А. В.
Гибридный алгоритм распознавания образов и его свойства // Вестник СибГАУ. — 2009. — Вып. 2(23). — С. 31-33. - Лапко А. В., Лапко В. А.
Непараметрическая оценка смеси плотностей вероятности, основанная на технологии размножения статистических данных // Вестник СибГАУ. — 2009. — Вып. 3(24). — С. 4-6. - Лебедев П. А., Лапко В. А., Варочкин С. С.
Непараметрические модели статических систем с линейной структурой // Сб. тр. VII Всерос. научн.-практ. конф. «Молодёжь и современные информационные технологии'". — Томск: ТПУ. — 2009. — С. 151–152 . - Саренков А. В., Лапко А. В.
Гибридные алгоритмы распознавания образов // Сб. тр. VII Всерос. научн.-практ. конф. «Молодёжь и современные информационные технологии». — Томск: ТПУ. — 2009. — С. 187–188 . - Капустин А. Н.
Многоуровневые непараметрические системы распознавания образов на основе декомпозиции обучающей выборки по её размерности: Автореф. дис. : канд. техн. наук. — Красноярск: ИВМ СО РАН. — 2009. — 20 с.
(Отдел прикладной информатики)
| К началу | |
Грант РФФИ №
Руководитель: д.ф.-м.н., профессор В. М. Белолипецкий
В меромектических озерах, к которым относится озеро Шира, горизонтальные неоднородности малы по сравнению с вертикальными. Вертикальные распределения гидрофизических и биофизических характеристик в глубоководной области озера хорошо описываются одномерными в вертикальном направлении математическими моделями. По разработанной компьютерной программе, основанной на одномерных в вертикальном направлении моделях, выполнена серия численных расчетов температуры, солености и плотности воды в озере Шира. Согласно натурным данным заглубления термоклина, халоклина и пикноклина для озера Шира практически совпадают и зависят от метеоданных и периода года. Из натурных и расчетных данных следует, что в озере Шира положение редокс-зоны совпадает со «ступенькой» плотности для осеннего и зимнего сезонов. Редокс-зона — это граница раздела слоев, насыщенных кислородом и сероводородом. Летом и весной редокс-зона находится существенно ниже пикноклина. Глубина расположения редокс-зоны является важной характеристикой стратифицированного водоема. В зависимости от того, сколько света проникает в редокс-зону, определяется видовой состав бактериального сообщества, формирующегося в этой зоне. В зоне перехода от аэробных слоев водной толщи к анаэробным (редокс-зона) обычно наблюдается повышенная активность планктонных сообществ.
Построено аналитическое решение для упрощенной модели стационарного ветрового течения (в вертикальной плоскости) в водоеме прямоугольной формы. Найдено аналитическое решение задачи о ветровом течении неоднородной жидкости в бассейне прямоугольной формы в приближении медленных течений. Разработанная компьютерная модель позволяет прогнозировать динамику вертикальных распределений температуры, солености, плотности воды и при необходимости других компонентов экосистемы в зависимости от метеоданных.
Основные публикации:
- Белолипецкий П. В., Белолипецкий В. М., Генова С. Н.
Численное моделирование годового режима вертикальной стратификации соленого озера Шира // Материалы Национальной конф. «Математическое моделирование в экологии». — Пущино: ИФХиБПП РАН. — 2009. — С. 34-35. - Белолипецкий В. М., Белолипецкий П. В., Генова С. Н.
Численное моделирование вертикальной структуры стратифицированного водоема // Тез. докл. всерос. конф. «Новые математические модели механики сплошных сред: построение и изучение». — Новосибирск. — 2009. — С. 33. - Компаниец Л. А., Якубайлик Т. В., Питальская О. С.
Аналитическое решение одной модели ветрового движения вязкой жидкости // Вычислительные технологии. — 2009. — Т. 14. — № 4. — С. 46-56.
(Отдел вычислительных моделей в гидрофизике)
| К началу | |
Грант РФФИ №
Руководитель: д.ф.-м.н., профессор М. В. Носков (ИКИТ СФУ)
Ответственный исполнитель от ИВМ СО РАН: д.т.н. К. В. Симонов
Разработана методика поиска возможных импактных структур на дне океана путём обработки гравиметрических и магнитометрических данных, поскольку анализ имеющихся данных по достоверным структурам позволяют утверждать, что метеоритный кратер характеризуется отрицательной аномалией гравитационного поля. Этот факт позволяет обнаруживать скрытые донные метеоритные кратеры путём анализа гравитационного и магнитного полей Земли. Предложено применение вейвлет-фильтрации для обнаружения кольцевых структур на дне океана. Обрабатывались цифровые данные рельефа и гравитационного поля. Разработанный алгоритм тестировался на известных импактных структурах: кратере Burkle на дне Индийского океана и кратере Чиксулуб (Мексиканский залив). После соответствующих этапов фильтрации кратеры отчетливо выделялись. Таким образом, показана возможность использования вейвлет-преобразования для поиска скрытых кольцевых структур импактного происхождения и выявления их особенностей, описана вычислительная методика обработки имеющихся геофизических данных, приведен алгоритм эффективной фильтрации пространственных данных.
Основные публикации:
- Noskov M. V., Simonov K. V.
Computer experiment in the problem on the recent traces of ocean cosmic impacts // Тр. X Междунар. семинара-совещания «Кубатурные формулы и их приложения». — Улан-Удэ: ВСГТУ. — 2009. — С. 72-79. - Marchuk An., Simonov K., Peretokin S.
The possible impact structures detection at the ocean bottom by gravimetric and magnetometric data processing // Int. Сonf. Asteroid-Comet Hazard-2009 (ACH-2009). — St. Petersburg, Russia. Book of abstracts. — St. Petersburg, 2009 — P. 123–124 .
(Отдел вычислительных моделей в гидрофизике)
| К началу | |
Грант РФФИ №
Руководитель: д.ф.-м.н., профессор О. В. Капцов
Предложен метод преобразования специальных линейных дифференциальных уравнений в частных производных с произвольным числом независимых переменных. Данный подход применяется для решения начально-краевых задач некоторых гиперболических уравнений. Развивается обобщение метода на системы линейных дифференциальных уравнений. Даны приложения данного подхода к модели неоднородной акустики и колебаниям неоднородных стержней переменного диаметра.
Основные публикации:
- Капцов О. В., Коростелев И. В.
Преобразования и решения линейных уравнений с переменными коэффициентами // Вычислительные технологии. 2009. — Т. 14. — № 4. — С. 28-45. - Капцов О. В.
Дифференциальные преобразования линейных уравнений с переменными коэффициентами // Тез. докл. междунар. конф. «Современные проблемы вычислительной математики и математической физики». — М: ВМК МГУ. — 2009. — С. 209.
(Отдел вычислительных моделей в гидрофизике)
| К началу | |
Грант РФФИ
Руководитель: д.ф.-м.н., профессор В. В. Денисенко
Построен многосеточный алгоритм для решения глобальной задачи электропроводности атмосферы. Решена задача о проникновении электрического поля из ионосферы до поверхности Земли в спокойных геомагнитных условиях. Показано, что электрическое поле вблизи поверхности Земли можно строить как решение одномерной по высоте задачи, но чтобы получить поля и токи в верхней атмосфере, необходимо решать трехмерную задачу.
Основные публикации:
- Nakamura R., Retino A., Baumjohann W., Volwerk M., Erkaev N., Klecker B., Lucek E. A., Dandouras I., Andre M., Khotyaintsev Y.
Evolution of dipolarization in the near-Earth current sheet induced by Earthward rapid flux transport // Ann. Geophys. — 2009. — Vol. 27. — P. 1743–175 4.
(Отдел вычислительной математики)
| К началу | |
Проект РФФИ №
Руководитель: д.ф.-м.н., профессор В. М. Садовский
В рамках теории малых деформаций идеально сыпучей среды с жесткими частицами построено точное решение, описывающее поля перемещений и напряжений в расширяющемся сферическом слое. При конечных деформациях задача сведена к нелинейной системе обыкновенных дифференциальных уравнений, решение которой получено с помощью численных методов. Аналогичные решения найдены в задаче для цилиндрического слоя. На их основе проанализировано влияние дилатансии сыпучей среды на напряженно-деформированное состояние вблизи расширяющихся полостей.
Разработан и программно реализован вычислительный алгоритм для исследования нестационарных сдвиговых течений сыпучей среды при конечных деформациях. Учитываются упругие свойства, характерные для уплотненного материала, и вязкие свойства, которые проявляются при его разрыхлении. Для описания напряженно-деформированного состояния в эйлеровых переменных применен тензор напряжений Коши и логарифмический тензор деформаций Генки. Анализ результатов расчетов показал, что такое сочетание приводит к адекватному описанию эффекта дилатансии среды при произвольной величине сдвига.
На основе математической модели моментной среды, по-разному сопротивляющейся растяжению и сжатию, исследован процесс однородного сдвига, сопровождающийся дилатансией материала. Серия расчетов, выполненных для различных значений параметров модели, показала, что в среде, в которой вращательное движение частиц влияет на изменение объема, дилатансионная кривая представляет собой немонотонную, волнообразную линию (рис. 45). Характерная длина волны на этой линии пропорциональна периоду вращательных колебаний частиц, который в сжатом состоянии среды существенно зависит от дилатансионных параметров и значительно отличается от периода колебаний в рыхлой среде.
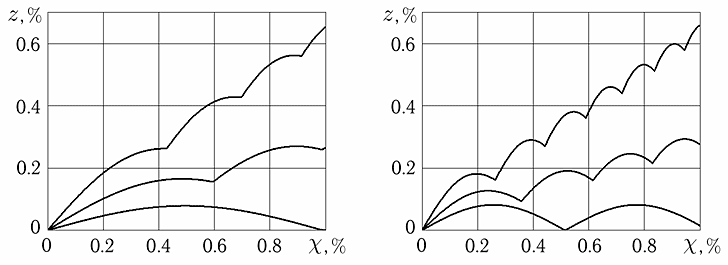
Рис. 45. Изменение зависимости объемной деформации среды от угла сдвига с увеличением параметра, моделирующего вклад сдвиговой деформации (кривые снизу вверх на каждом из графиков), и с увеличением параметра, характеризующего вклад вращательного движения частиц (слева направо)
Основные публикации:
- Садовский В. М.
Радиальное расширение сыпучей среды в сферическом и цилиндрическом слоях // ПМТФ. — 2009. — Т. 50. — № 3. — С. 190–196 . - Мясников В. П., Садовский В. М.
Вариационные принципы теории предельного равновесия разнопрочных сред // В. П. Мясников. Избранные труды «Механика технологических процессов». -Владивосток: Дальнаука. — 2008. — Т. 3. — С. 184–196 . - Садовская О. В., Садовский В. М.
Математическое моделирование течений сыпучей среды // Сб. тез. докл. всерос. конф. «Новые математические модели в механике сплошных сред: построение и изучение». — Новосибирск: ИГнЛ СО РАН. — 2009. — С. 126–127 .
(Отдел вычислительной механики деформируемых сред)
| К началу | |
Грант РФФИ №
Руководитель: член-корреспондент РАН В. В. Шайдуров
1. Многосеточные итерационные методы. Исследовалась сходимость многосеточных итерационных методов для решения сеточной задачи, полученной дискретизацией эллиптического уравнения второго порядка с помощью кусочно-линейных элементов на треугольниках с использованием численного интегрирования. Обычно сходимость многосеточных методов обосновывается в предположении, что элементы матрицы и вектора правой части системы уравнений метода конечных элементов вычислены точно. Однако на практике они, как правило, вычисляются с использованием квадратурных формул.
Рассмотрены полный многосеточный метод на основе W-цикла и каскадный алгоритм, представляющий собой наиболее простую версию многосеточных методов. Предложен способ построения дискретных задач на более грубых сетках. Доказано, что для обоих алгоритмов число арифметических операций, приходящихся на одно неизвестное, для определения приближенного решения с точностью, совпадающей по порядку с погрешностью дискретной задачи с учетом численного интегрирования, не зависит от числа неизвестных и количества сеток.
2. Построение согласованных триангуляций двумерных многосвязных областей. Задача сеточного разбиения акватории Мирового океана до сих пор далека от полного решения. Сложность решаемой проблемы в первую очередь связана с задачей описания области Ω, поскольку задать рельеф дна и контуры границ непосредственно по навигационным картам трудно из-за обширности Ω. Поэтому для построения сетки использованы батиметрические базы данных серии ETOPO, которые можно свободно получить на интернет-сайте Национального центра геофизических данных США по адресу http://www.ngdc.noaa.gov/mgg/global/global.html.
Построен алгоритм дискретизации связной части Ωh акватории Ω по заданной минимальной глубине h ≥ 0 и заданным наименьшему и наибольшему шагам сетки со сгущением сетки около береговой линии. При этом элементами дискретизации могут являться квадраты как на (рис. 46) или равнобедренные прямоугольные треугольники (рис. 47), а необходимая батиметрическая информация получена только из анализа данных базы ETOPO. Отметим, что переход от квадратной сетки к треугольной осуществляется методом шаблонов. В случае необходимости более точного описания границы расчетной области можно провести граничную коррекцию построенной сетки. Необходимо отметить большую скорость работы предложенного алгоритма: в реальных расчётах с применением базы ETOPO2 время дискретизации акватории Мирового океана на ПК класса Pentium IV с тактовой частотой 1,5 Ггц составляло не более 10 сек., включая считывание батиметрических данных и запись вычисленных параметров сетки.
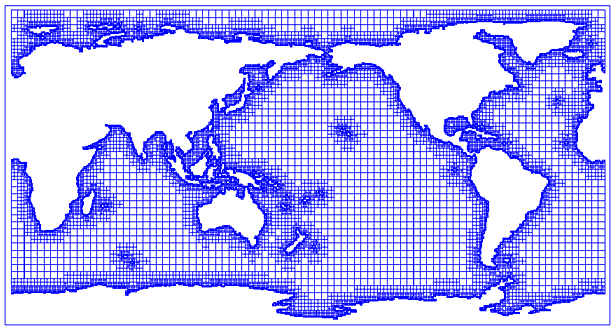
Рис. 46. Дискретизация квадратами для границы акватории на глубине h = 0. Число элементов 26063, число узлов 14716
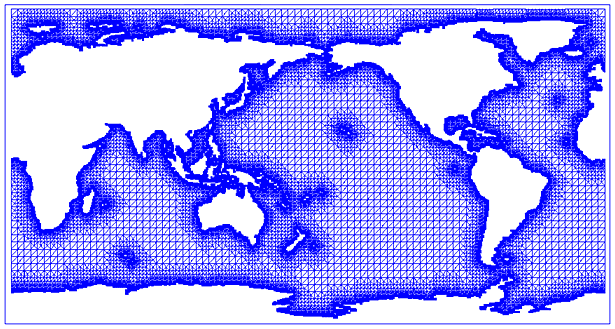
Рис. 47. Дискретизация Ωh треугольниками для h = 0. Число элементов 65777, число узлов 36834
В 2009 году разработан алгоритм разбиения двумерных многосвязных областей на треугольники, идея которого подсказана алгоритмом построения «салфетки Серпинского», представляющей собой один из классических примеров фрактальной геометрии. В основе предлагаемого алгоритма триангуляции, результатом работы которого является последовательность неравномерных вложенных друг в друга сеток, лежит единственность представления прямоугольного равнобедренного треугольника в виде объединения двух прямоугольных равнобедренных треугольников, как изображено на рис. 48.
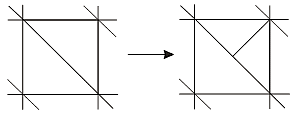
Рис. 48. Шаблон для прямоугольного треугольника
Как и в методе граничной коррекции, исходную многосвязную двумерную область Ω помещаем в прямоугольник R, который изначально разбит на небольшое количество равнобедренных прямоугольных треугольников. Удобно ввести понятие уровня вложенности треугольника. Треугольникам начального разбиения приписываем нулевой уровень вложенности. Треугольники, полученные бисекцией из треугольников нулевого уровня, имеют первый уровень вложенности и т.д. Аналогично методу шаблонов, в котором в качестве базового элемента взят равнобедренный прямоугольный треугольник, шаблоном для которого является указанное выше представление в виде объединения двух равных треугольников, полученных из исходного бисекцией, триангулируем объемлющий прямоугольник R, после чего при помощи граничной коррекции получаем сетку для области Ω. Обратный процесс — процесс перехода к предыдущему уровню вложенности, вплоть до нулевого, основан на структурированности построенной триангуляции. Этот процесс осуществляется посредством укрупнения треугольников самого высокого (на данном этапе) уровня вложенности и продемонстрирована на рис. 49.
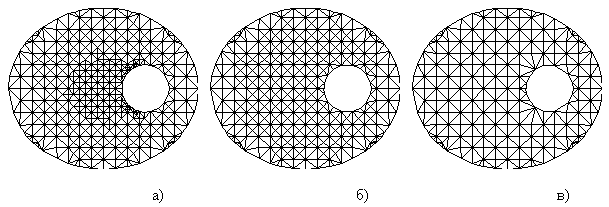
Рис. 49. Процесс объединения: а) наивысший уровень вложенности треугольников; б) сетка после одного шага алгоритма; в) сетка после двух шагов алгоритма укрупнения
Описанный процесс объединения, т.е. переход к предыдущим уровням вложенности вплоть до нулевого, может играть существенную роль в уменьшении временных затрат на решение систем линейных алгебраических уравнений (СЛАУ) в методе конечных элементов, построенных на базе предложенной триангуляции. Так, например, в методе Гаусса в качестве ведущих элементов глобальной матрицы жёсткости можно брать её диагональные элементы в порядке, обратном порядку появления узлов сетки в процессе её построения по предлагаемому алгоритму. По точности результаты незначительно отличаются от решения СЛАУ методом Гаусса с выбором максимального элемента по столбцу, однако полученная в ходе процесса исключения матрица является более разреженной, чем аналогичная матрица из метода Гаусса. Кроме того, вложенность сеток позволяет реализовать метод Холецкого решения СЛАУ без предварительного формирования глобальной матрицы, проводя исключения искомых узловых значений из локальных матриц жёсткости.
3. Исследование эффективности параллельных реализаций метода конечных элементов для начально-краевой задачи мелкой воды. На примере численного решения начально-краевой задачи для уравнений мелкой воды в отчетный период рассмотрены технологические аспекты разработки масштабируемых параллельных алгоритмов для кластерных вычислительных систем с использованием библиотеки MPI.
Для реализации параллелизма по данным были разработаны алгоритмы декомпозиции вычислительной области с триангуляцией для модельных задач в прямоугольнике на сфере.
Численные эксперименты показали, что использование неблокирующего режима обменов, которое допускается алгоритмом, является, безусловно, более эффективным. Поскольку в вычислительном плане рассмотренные варианты декомпозиции области равноценны, то следует отметить как явное преимущество простоту организации параллельного алгоритма при декомпозиции без теневых граней для неструктурированных триангуляций реальных акваторий.
Особый интерес представляют результаты исследования зависимости ускорения параллельной программы от архитектуры кластера. Расчеты были проведены на трех высокопроизводительных ВС различных архитектур: кластере собственной сборки ИВМ СО РАН; кластере СКИФ Cyberia T-Platform Межведомственного вычислительного центра ТГУ и кластере Hewlett-Packard информационно-вычислительного центра НГУ. Показано преимущество однородного устройства кластера (СКИФ Cyberia и HP-кластер ИВЦ НГУ) над гетерогенным (кластер ИВМ СО РАН). Кроме того, продемонстрирована неустойчивость ускорения при неоднородном составе кластера, которая не присуща ни алгоритму, ни реализации.
Исследование времени выполнения обменов в неблокирующем режиме на реальных расчетах при однородной архитектуре кластера показало следующее:
- время обменов минимально и не зависит от количества процессов, участвующих в обменах, если загружены все ядра на узле (по одному процессу на ядро);
- при наличии при расчетах не полностью загруженных узлов, время обменов тем больше, чем больше количество простаивающих ядер;
- время, затраченное на обмены, уменьшается с ростом количества задействованных процессов (т.е. уменьшением времени вычислений).
4. Применение метода решеточных уравнений Больцмана с распараллеливанием для решения прикладных задач. Для решения дискретных уравнений Больцмана был реализован двухшаговый алгоритм расщепления: сначала находились промежуточные значения функций распределения в результате только столкновений частиц, а затем промежуточные функции модифицировались для учета «свободного полета» частиц. Использовался язык параллельного программирования Fortran-DVM, разработанный в ИПМ им. М. В. Келдыша РАН. Расчеты выполнялись на кластере МВС-100K (МСЦ РАН), имеющем 990 вычислительных узлов, которые содержат суммарно 7920 процессорных ядер.
В отчетном году выполнялась разработка численного алгоритма и написание программы для параллельных расчетов. На примере тестовой задачи (течение вязкой несжимаемой жидкости в кубической области с подвижной верхней стенкой) проведено сравнение решений, полученных в данной работе, с решениями, опубликованными в литературе другими авторами, и при использовании ими «традиционных» методов. Показано хорошее совпадение результатов. Распараллеливание позволяет за разумное машинное время проводить расчеты на очень детальных сетках, состоящих из сотен миллионов и миллиардов узлов. Например, на расчетной сетке (768 x 768 x 768), в которой 453 млн. узлов, при использовании 768-ми процессоров за 7.9 минуты машинного времени было сделано 1000 шагов по «задачному» времени. А на сетке (1536 x 1536 x 1536) (3.6 млрд. узлов) при использовании 1728-ми процессоров на 1000 шагов потребовалось 31.8 минуты машинного времени.
5. Разработка методов типа Рунге-Кутты для решения получаемы систем ОДУ. Разработан алгоритм определения коэффициентов полиномов устойчивости явных методов типа Рунге-Кутты, при которых метод имеет для области устойчивости заданную форму и размер. Для произвольного m получены коэффициенты явных m-стадийных методов типа Рунге-Кутты первого и второго порядка точности. Области устойчивости промежуточных численных формул согласованы с областью устойчивости основной схемы. Построены неравенства для контроля точности и устойчивости.
Получены коэффициенты явных двухстадийного и трехстадийного методов типа Рунге-Кутты. Построены неравенства для контроля точности вычислений и устойчивости численной схемы. Для данных методов второго и третьего порядков точности на основе стадий данных численных схем достроены методы первого порядка точности, области устойчивости которых расширены до 8 и 18, соответственно. Сформулированы два алгоритма интегрирования переменного порядка и шага, в которых наиболее эффективная схема выбирается из критерия устойчивости. Проведенные тестовые испытания показывают примерно семикратное преимущество алгоритмов переменного порядка по сравнению с расчетами по фиксированной схеме.
Разработан алгоритм формирования правой части и матрицы Якоби дифференциальных уравнений химической кинетики. С помощью построенных выше алгоритмов интегрирования проведено численное моделирование пиролиза этана, ионизационно-деионизационного цикла цезия в верхней атмосфере и модифицированного орегонатора, дающего сложный предельный цикл.
На основе двухстадийной схемы типа Рунге-Кутты и L-устойчивого (2,1)-метода второго порядка точности разработан алгоритм интегрирования переменного порядка, шага и переменной структуры, в котором на каждом шаге выбирается наиболее эффективная явная или L-устойчивая численная схема исходя из критерия устойчивости. Результаты расчетов подтверждают эффективность построенного алгоритма при невысокой точности расчетов.
Основные публикации:
- Gileva L. V., Shaidurov V. V.
Convergence of a full multigrid algorithm for quadratic finite elements in a domain with a curvelinear boundary // Rus. Journ. of Num. Anal. and Math. Model. — 2009. — Vol. 24. — № 5. — P. 425–438 . - Гилева Л. В.
Многосеточные итерационные алгоритмы в методе конечных элементов с учетом численного интегрирования // Вычислительные технологии. — 2009. — Т. 14, № 1. — С. 34-51. - Киреев И. В., Пятаев С. Ф.
Пиксельная технология дискретизации акватории Мирового океана // Вычислительные технологии. — 2009. — Т. 14. — № 5. — С. 30-39. - Kamenshchikov L. P.
Parallel Implementation of Lattice Boltzmann Flow Simulation in Fortran-DVM Language // Proceedings of 10th Int. Conf. «Parallel Computing Technologies» (PaCT-2009), LNCS 5698, Springer-Verlag Berlin Heidelberg. — Novosibirsk, Russia. — 2009. — P. 216–225 . - Карепова Е. Д., Шайдуров В. В., Вдовенко М. С.
Параллельные реализации метода конечных элементов для краевой задачи для уравнений мелкой воды // Вестник ЮУрГУ. Серия «Математическое моделирование и программирование». — 2009. — Вып. 3. — № 17 (150). — С. 73-85. - Карепова Е. Д., Шайдуров В. В.
Параллельная реализация МКЭ для начально-краевой задачи мелкой воды // Вычислительные технологии. — 2009. — Т.14. — № 6. — С. 45-57. - Кнауб Л. В., Новиков Е. А.
Алгоритм интегрирования на основе явного трехстадийного метода Рунге-Кутта // Вестник КрасГАУ. — 2009. — № 3. — С. 49-54. - Кнауб Л. В., Новиков Е. А.
Алгоритм интегрирования с контролем точности и устойчивости явного трехстадийного метода типа Рунге-Кутта // Системы управления и информационные технологии. — 2009. — № 1(35). — С. 20-24. - Кнауб Л. В., Новиков Е. А.
Применение явного трехстадийного метода типа Рунге-Кутта для численного моделирования задач химической кинетики // Вестник СибГАУ. — 2009. — № 1(22). — Ч. 1. — С. 77-80. - Кнауб Л. В., Новиков Е. А.
Численное моделирование орегонатора двухстадийным методом типа Рунге-Кутта // Вестник КрасГАУ. — 2009. — № 4. — С. 50-56. - Новиков A. Е., Новиков E. A.
Численное решение жестких задач с небольшой точностью // Математическое моделирование. — 2009. — Т. 21, № 11. — С. 31-44. - Новиков E. A.
Конструирование областей устойчивости явных методов типа Рунге-Кутта // М.: Вычислительные методы и программирование. — 2009. — Т. 10. — С. 248–257 . - Новиков E. A.
Согласование областей устойчивости явных методов решения задач умеренной жесткости // Известия Челябинского научного центра УрО РАН. — 2009. — № 43. — С. 6-10.
(Отдел вычислительной математики)
| К началу | |
Грант РФФИ №
Руководитель: к.б.н. Л. Г. Бондарева (Институт биофизики СО РАН)
Исполнители от ИВМ СО РАН: д.ф.-м.н., профессор В. М. Белолипецкий, к.т.н., доцент С. Н. Генова
Рассматривается задача о загрязнении водной речной системы техногенными радионуклидами. Исследование ограничивается абиотической формой переноса веществ. В речных системах трансурановые элементы (ТУЭ) могут находиться в растворенном виде и сорбироваться компонентами водной системы. В растворенном виде ТУЭ распространяются на значительные расстояния. В нерастворенной форме ТУЭ переносятся взвешенными и донными наносами. Выделяются основные механизмы, определяющие перенос загрязнений речными потоками: перенос взвешенных наносов водным потоком; осаждение частиц на дно; взмучивание мелких фракций из донных отложений.
В зависимости от расхода воды, геометрии речного русла изменяется скорость течения, которая определяет перенос взвешенных наносов и процессы взмучивания-осаждения. Для оценки накопления радионуклидов в донных отложениях используется математическая модель работы [Белолипецкий В. М., Генова С. Н. Вычислительный алгоритм для определения динамики взвешенных и донных наносов в речном русле // Вычислительные технологии. — 2004. — Т. 9. — № 2. — С. 9-25].
Рассматривается участок реки Енисей, примыкающий к створу поступления загрязнений. Часть загрязнений поступает в растворенном виде, другая — в нерастворенной форме, сорбированной взвешенными наносами. Предполагается, что концентрации радионуклидов на твердых частицах пропорциональны площадям поверхности частиц. С использованием натурных данных оцениваются распределения радионуклидов по фракциям в начальном створе. Затем определяются перенос и осаждение частиц вдоль русла. Результаты расчетов сравниваются с данными натурных измерений.
Основные публикации:
- Белолипецкий В. М., Генова С. Н.
Численная модель переноса техногенных радионуклидов в речных потоках (на примере р. Енисей) // Тез. междунар. конф. «Современные проблемы вычислительной математики и математической физики». — Москва. — 2009. — С. 296–297 .
(Отдел вычислительных моделей в гидрофизике)
| К началу | |
Грант РФФИ №
Руководитель: д.ф.-м.н., профессор В. К. Андреев
1. Получены точные решения, описывающие стационарное течение двух вязких теплопроводных несмешивающихся жидкостей с общей поверхностью раздела в наклонном канале при совместном действии градиента давления, термокапиллярных и массовых сил. Исследована устойчивость полученных решений относительно плоских и пространственных возмущений. Изучено влияние направления продольного градиента температуры и ориентации системы относительно силы тяжести на устойчивость течения. Имеет место смена форм неустойчивости при различных режимах.
2. Методами численного моделирования проведено комплексное исследование задачи о смешивании бинарной смеси в прямоугольной области при условиях пониженной гравитации в быстроменяющемся внешнем горизонтальном силовом поле. Рассмотрено начальное состояние системы с наличием узкой поверхности раздела двух компонентов смеси, что соответствует условию устойчивого равновесия.
В зависимости от параметров задачи обнаружены различные режимы течения. Наибольший эффект в динамике развития течения наблюдается при изменении аспектного отношения AR cторон расчетной области. Так при AR > 1.75 происходит потеря устойчивости границы раздела жидкостей с проявлением ее существенной деформации и интенсивным перемешиванием компонентов смеси. С уменьшением аспектного отношения достигается обратный эффект — происходит стабилизация структуры течения, а процесс смешивания компонентов уменьшается в пределе до диффузионных порядков.
3. Исследована применимость приближения Буссинеска к задачам термовибрационной конвекции в замкнутых областях. Рассматриваются вибрационные движения с высокой частотой и малой амплитудой, что позволяет эффективно использовать метод осреднения физических величин по периоду колебаний. Получены оценки скорости осредненного движения вида
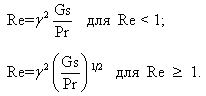
Здесь Re — число Рейнольдса для осредненного течения, Gs — число Гершуни (вибрационное число Рэлея), характеризующее вибрационное воздействие, Pr — число Прандтля, γ — коэффициент пропорциональности (отношение осредненной скорости к пульсационной скорости). Найденные оценки подтверждены численными расчетами вибрационной конвекции в квадратной полости (рис. 50). Полученные оценки были использованы для вывода критериев, гарантирующих справедливость приближения Буссинеска. Основные предположения данного приближения применены к уравнениям сохранения массы, импульса и энергии для сжимаемой вязкой теплопроводной жидкости (газа). Учитывается вклад вязкой диссипации и работы сил давления в баланс энергии. Анализ порядка величин различных членов в уравнениях движения приводит к семи безразмерным параметрам, малость которых гарантирует справедливость приближения Буссинеска. Данные результаты представляют важную информацию для дальнейших численных и аналитических исследований вибрационных явлений в жидкостях.
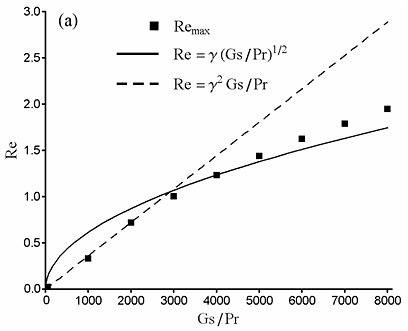
Рис. 50. Зависимость числа Рейнольдса от отношения Gs/Pr (сплошная и штрихованная линии — оценки, точки — результаты численных расчетов)
4. Описаны возможные режимы стационарных течений в жидком цилиндре, обдуваемом потоком газа. Исследована устойчивость этих режимов по отношению к малым возмущениям нормальной формы. Обнаружено, что критическое число Марангони уменьшается в случае, когда направление прокачки газа совпадает с направлением термокапиллярного течения на границе раздела и увеличивается в противоположном случае. Показана возможность остановки течения в жидкости потоком газа.
Основные публикации:
- Gaponenko Y., Shevtsova V.
High frequency vibration effect on the water-isopropanol mixture // EUROTHERM, Seminar Nr. 84. — Namur, Belgium. — 2009. — 4 p. - Ryzhkov I. I., Gaponenko Y. A.
On the Boussinesq approximation in vibrational convection problems // Physics of Fluids. — 2009 (in press). - Андреев В. К., Собачкина Н. Л.
Свойства решений начально-краевой задачи, возникающей при движении бинарной смеси в цилиндрической трубе // Препринт № 2. — Красноярск: ИВМ СО РАН. — 2009. — 40 с. - Андреев В. К., Бекежанова В. Б., Ефимова М. В., Рыжков И. И., Степанова И. В.
Неклассические модели конвекции: точные решения и их устойчивость // Вычислительные технологии. — 2009. — Т. 14. — № 6. — С. 5-18.
(Отдел дифференциальных уравнений механики)
| К началу | |
Грант РФФИ №
Руководитель: д.ф.-м.н., профессор В. П. Шунков
Охарактеризованы периодические группы Шункова. Получены результаты для слойно конечных групп с заданным спектром и некоторыми дополнительными условиями.
Получено новое доказательство ослабленной проблемы Бернсайда, использующее только теоретико-групповые рассуждения, в отличие от ранее полученного доказательства при помощи аппарата алгебр. Ослабленную проблему Бернсайда для периода pn, где p — простое число, решил Е. И. Зельманов. Но его доказательство слишком сложно: пронизано громоздкими формулами из теории алгебр Ли. Пусть Fs — свободная группа с числом свободных порождающих s не меньшего двух, и фактор-группа
Теорема. Число конечных групп вида
В. И. Сенашовым изучались бесконечные группы с условием почти слойной конечности нормализаторов конечных нетривиальных подгрупп. Найдены условия, при которых почти слойная конечность распространяется с нормализаторов нетривиальных конечных подгрупп группы на всю группу G. Доказана
Теорема. Пусть группа Шункова G содержит сильно вложенную подгруппу, обладающую черниковской почти слойно конечной периодической частью. Если в G нормализатор любой нетривиальной конечной подгруппы обладает почти слойно конечной периодической частью, то сама группа G обладает почти слойно конечной периодической частью.
Заметим, что ранее рассматривались группы Шункова лишь при условии почти слойной конечности всех собственных подгрупп и при условии периодичности для группы.
Найдены все выпуклые многогранники с нулевой кривизной каждой вершины и с гранями, составленными из правильных многоугольников, либо являющимися такими многоугольниками. Дано описание выпуклых многогранников, которые обладают вершинами с нулевой кривизной, т.е. сумма плоских углов граней в таких вершинах равна 360 градусов. Построены новые примеры таких тел, названных m-правильногранниками. Найдены все несоставные правильногранники, которые являются составными m-правильногранниками.
При помощи системы компьютерной алгебры вычислены пересечения силовских 2-подгрупп в группе автоморфизмов группы U4(3), чем дополнены исследования В. И. Зенкова из ИММ УрО РАН и частично решена проблема 14.69 из «Коуровской тетради» о минимуме числа таких порождающих конечную простую группу инволюций, что их произведение равно единице.
Основные публикации:
- Сенашов В. И.
О группах Шункова с сильно вложенной подгруппой // Труды ИММ УрО РАН. — 2009. — С. 203–210 . - Сенашов В. И.
Одна характеризация групп с почти слойно конечной периодической частью // Тез. докл. междунар. конф. «Мальцевские чтения». — Новосибирск: ИМ СО РАН. — 2009. — С. 82. - Сенашов В. И.
О спектре группы // Препринт № 4 «Алгебраические системы». — Красноярск: ИВМ СО РАН. — 2009. — С. 7-17. - Сенашов В. И.
О группах, обладающих сильно вложенной подгруппой // Тр. междунар. алгебр. конф. «Алгебра и ее приложения». — Нальчик: Каб.-Балк. ун-т. — 2009. — С. 118–120 . - Senashov V. I., Iakovleva E. N.
Properties of groups with points // Mashad J. Math. Sci. — 2009. — Vol. 2. — № 1. — P. 13-23. - Senashov V. I.
Сharacterizations of Layer-Finite Groups and Their Extensions // J. of Siberian Federal University // Mathematics and Physics. — 2009. — № 2(3). — P. 279–287 . - Тимофеенко А. В.
О приложениях групп симметрий // Тез. докл. междунар. конф. «Геометрия в «целом», топология и их приложения. — Харьков: Физико-технический институт низких температур НАН Украины. — 2009. — С. 42. - Тимофеенко А. В.
Выпуклые многогранники с паркетными гранями // Доклады АН. — 2009. — Т. 428. — № 4. — С. 454–457 . - Тимофеенко А. В.
О соединении несоставных многогранников // Алгебра и анализ. — 2009. — Т. 21. — № 3. — С. 165–209 . - Timofeenko A. V.
Convex Polyhedra with Parquet Faces // Doklady Mathematics. — 2009. — Vol. 80. — № 2. — P. 720–723 . - Timofeenko A. V.
The non-platonic and non-Archimedean noncomposite polyhedra // J. of Mathematical Sciences. — 2009. — Vol. 162. — № 5. — P. 710–729 . - Шунков В. П.
О спектре группы // Препринт № 4 «Алгебраические системы». — Красноярск: ИВМ СО РАН. — 2009. — С. 3-6.
(Отдел дифференциальных уравнений механики)
| К началу | |
Грант РФФИ №
Руководитель: д.ф.-м.н., профессор А. Н. Горбань
Конференция проводилась со 2 по 4 октября 2009 года в Институте вычислительного моделирования СО РАН. Научная программа конференции включала следующие секции: архитектура и алгоритмы обучения нейронных сетей, нейросетевые экспертные системы, нейросетевое программное обеспечение и принципы его построения, нейросетевые технологии производства знаний, нейросетевые методы в медицине, анализ данных. На конференции были представлены 70 докладов от 109 участников из 23 городов Российской Федерации и СНГ. Принято решение о продолжении ежегодного проведения семинаров с расширением тематики конференции за счет специалистов, занимающихся обработкой и анализом данных с привлечением большего числа студентов и молодежи.
Основные публикации:
- Нейроинформатика и ее приложения // Материалы ХVII Всерос. семинара «Нейроинформатика, ее приложения и анализ данных «. — Красноярск: ИВМ СО РАН. — 2009. — 180 c.
(Отдел моделирования неравновесных систем)
| К началу | |
Грант РФФИ №
Руководитель: д.ф.-м.н., профессор В. В. Слабко
Конференция проводилась с 9 по 11 октября 2009 года в Институте вычислительного моделирования СО РАН. Научная программа конференции включала следующие секции: методы и технологии математического моделирования неравновесных систем; разработка математического и программного обеспечения моделирования нелинейных, нестационарных и неоднородных по пространству процессов; развитие методов имитационного моделирования сложных систем (классическое имитационное моделирование, нейронные сети, моделирование с использованием активных сред и т.п.); приложения в физике, химии, технике, биологии, медицине, экономике и финансах. На семинаре был представлен 71 доклад от 88 участников из 20 городов различных регионов Российской Федерации и СНГ. Целью семинара было обсуждение и распространение современных достижений в области применения математических методов для моделирования неравновесных систем различной природы (неравновесных систем, изучаемых в различных областях науки: физике, химии, биологии, медицине, экономике и финансах). В ходе заключительной дискуссии принято решение провести следующий, 13-й семинар МНС-10 в октябре 2010 г.
Основные публикации:
- Моделирование неравновесных систем — 2009 // Материалы ХII Всерос. семинара «Моделирование неравновесных систем». — Красноярск: ИВМ СО РАН. — 2009. — 224 с.
(Отдел моделирования неравновесных систем)
| К началу | |
Грант РФФИ №
Руководитель: д.ф.-м.н. О. В. Капцов
В монографии представлен ряд методов построения точных решений линейных и нелинейных уравнений с частными производными. Изложение ведется в рамках двух основных парадигм — непрерывные преобразования и инвариантность. Особое внимание уделяется таким подходам, как методы интегрирования Дарбу, Эйлера, Беклунда, Мутара. Дано обобщение классических методов для систем дифференциальных уравнений, подробно описан новый способ интегрирования — метод линейных определяющих уравнений. С характеристиками систем уравнений связываются инвариантные тензоры и интегральные инварианты, обсуждаются локальные законы сохранения. В качестве приложений рассмотрены математические модели механики сплошной среды: от гидродинамики до нелинейной теплопроводности.
Монография прошла корректуру и вышла в издательстве ФИЗМАТЛИТ (Москва).
(Отдел вычислительных моделей в гидрофизике)
| К началу | |
Грант РФФИ №
Руководитель: д.ф.-м.н., профессор Н. В. Еркаев
Разработана магнитогидродинамическая модель «флэппинг» колебаний токового слоя магнитосферного хвоста с учетом эффектов Холла. В линейном приближении получены решения, соответствующие различным распределениям плотности тока и плотности плазмы поперек токового слоя.
Найдены дисперсионные зависимости собственных частот от волнового числа для различных мод колебаний. Получены оценки частот и групповых скоростей волн для типичных условий плазменного слоя магнитосферного хвоста. Найденные значения удовлетворительно согласуются с экспериментом.
Разработана аналитическая модель квазистационарного магнитного пересоединения в бесстолкновительной плазме в рамках холловского магнитогидродинамического приближения. Показано, что проблема сводится к решению задачи Града-Шафранова относительно магнитного потенциала. Аналитическое решение сравнивается с результатами численного эксперимента (метод частиц в ячейках). Сопоставление распределений электрических токов в области магнитного пересоединения, а также картин магнитного и электрического полей показывает хорошее согласие аналитической теории с численным экспериментом, выполненным методом «частиц в ячейках».
Выполнен анализ экспериментальных данных, полученных на борту космических аппаратов Cluster, когда они находились в пределах тонкого токового слоя магнитосферного хвоста. Были зарегистрированы потоки ускоренной плазмы в направлении к Земле, а также изгибные «флэппинг» осцилляции токового слоя, распространяющиеся в направлении вечернего фланга магнитосферы. Данные указывают на причинно-следственную связь между «флэппинг» колебаниями и ускоренными потоками плазмы в направлении к Земле.
Основные публикации:
- Erkaev N. V., Semenov V. S., Kubyshkin I. V., Kubyshkina M. V., Biernat H. K.
MHD aspect of current sheet oscillations related to magnetic field Gradients // Ann. Geophys. — 2009. — Vol. 27. — P. 417–425 . - Semenov V., Korovinskiy D., Divin A., Erkaev N., Biernat H.
Collisionless magnetic reconnection: analytical model and PIC simulation comparison. // Ann. Geophys. — 2009. — Vol. 27. — P. 905–911 .
(Отдел вычислительной математики)
| К началу | |
Грант РФФИ-ККФПНиНТД
Руководитель: к.ф.-м.н., доцент О. Э. Якубайлик
В работе рассматриваются методы комплексного стратегического планирования и управления пространственным развитием региональной экономики, основанные на использовании современных информационных технологий и средств геоинформационного моделирования. Предложенный в рамках проведенного исследования подход, базирующийся на выявлении источников формирования конкурентных преимуществ территории, позволил осуществить комплексную количественную оценку достигнутого каждым регионом уровня конкурентоспособности и выявить ключевые направления его роста. Разработано программно-технологическое обеспечение, соответствующая методика и формат описания, ввода и первичной обработки данных для геоинформационной модели управления территориальным развитием, предназначенной для оценки развития экономики территорий интенсивного промышленного освоения природных ресурсов Красноярского края (рис. 51).
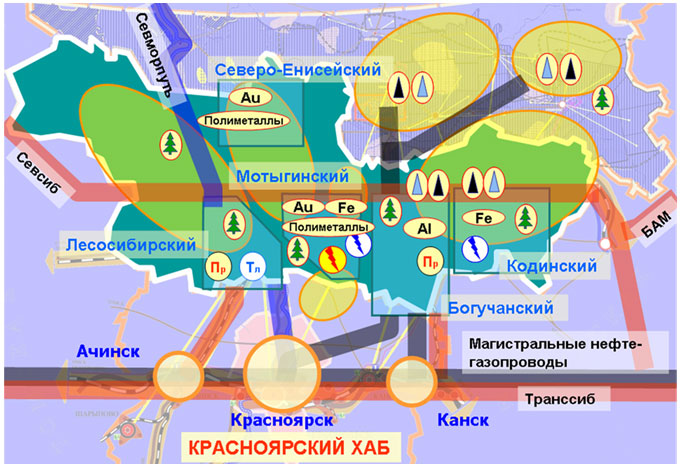
Рис. 51. Ресурсы и транспортная инфраструктура определяют структурно-функциональную организацию экономики Нижнего Приангарья
Основные публикации:
- Якубайлик О. Э.
Геоинформационная интернет-система мониторинга состояния окружающей природной среды в зоне действия предприятий нефтегазовой отрасли // Вестник СибГАУ. — 2009. — Вып. № 4 (25). - Замай С. С., Желиховская В. В., Шалахина Д. Х. Якубайлик О. Э.
Практика и планы создания информационных систем регулирования градостроительной деятельности и стратегического управления региональным развитием Красноярского края // Материалы XI Всерос. научн.-практ. конф. «ПИР-2009». — Красноярск: РИЦ СибГТУ. — 2009. — С. 50-53.
(Отдел вычислительной физики)
| К началу | |
Проект МК-299.2009.1 «Структуры и устойчивость конвективных течений в многокомпонентных смесях и двухфазных системах»
Руководитель: к.ф.м.н. И. И. Рыжков
Термокапиллярные течения (т. е. движения, вызванные силой поверхностного натяжения) возникают во многих естественных и технологических процессах. Одним из таких процессов является выращивание кристаллов методом зонной плавки. Для изучения процессов, происходящих в расплавленной зоне, широко используется модель жидкого моста. Эта модель представляет собой жидкий цилиндр, помещенный между двумя стержнями с различной температурой. Наличие градиента температуры на свободной границе приводит к возникновению термокапиллярного течения, которое направлено от нагретого к холодному стержню и является стационарным при небольших разностях температур. При достижении критической разности температур стационарное движение становится неустойчивым. Наличие подобных неустойчивостей в зоне расплава может существенно повлиять на качество кристалла.
Одним из методов управления устойчивостью стационарного движения является обдувание жидкого моста потоком газа. Взаимодействие механических напряжений на границе раздела может влиять на устойчивость системы в зависимости от направления прокачки газа и термокапиллярного течения жидкости на границе раздела.
В рамках данного проекта было проведено теоретическое исследование термокапиллярных течений в двухфазной системе, состоящей из бесконечного жидкого цилиндра, обдуваемого потоком газом (рис. 52 а). Слой газа ограничен внешней твердой стенкой. Найдено точное решение, описывающее стационарное движение и исследованы возможные режимы течений (рис. 52 б).
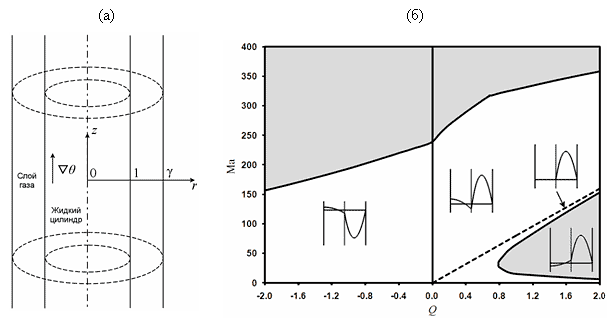
Рис. 52. (а) Жидкий цилиндр, окруженный слоем газа. (б) Режимы течения (показаны профили скорости в жидкости и газе) в зависимости от расхода газа Q и их устойчивость (в заштрихованной области течение неустойчиво)
Изучена устойчивость данных режимов по отношению к малым возмущениям (трехмерные нормальные возмущения). Карта устойчивости системы приведена на рис. 52 б).
Показано, что если направление прокачки газа совпадает с направлением термокапиллярного течения на границе раздела (расход газа Q < 0), то граница устойчивости (критическое число Марангони Мa) понижается по сравнению со случаем Q = 0. При изменении направления прокачки на противоположное (Q > 0) устойчивость системы повышается. Увеличение расхода при фиксированном значении числа Марангони приводит к подавлению термокапиллярного течения в жидкости потоком газа (пунктирная линия на рис. 52 б). При дальнейшем увеличении Q направление термокапиллярного движения на границе раздела меняется. Данный режим является устойчивым при небольших числах Марангони и расходах газа.
Основные публикации:
- Ryzhkov I. I., Shevtsova V. M.
Interfacial flow control in two-phase systems with application to liquid bridges // Abstracts of 62nd Annual Meeting of the APS Division of Fluid Dynamics. — 2009. AQ.00003. - Рыжков И. И.
Устойчивость конвективного течения в жидком цилиндре при спутном потоке газа // МЖГ. — 2009 (принята в печать).
(Отдел дифференциальных уравнений механики)
| К началу | |
Грант Фонда содействия отечественной науке по программе «Кандидаты и доктора наук РАН»
Руководитель: к.т.н., доцент Н. А. Чернякова
В ранее предложенной модифицированной вероятностной модели роста усталостных трещин, в случае двухчастотного и двухосного нагружения, учитывается структурная неоднородность «процесс-зоны» на фронте разрушения. Структурная неоднородность характеризуется отношением размера зерна металла к радиусу зоны пластических деформаций в вершине трещины. Процесс роста трещины представляется как двухстадийный: на первой стадии происходит образование микротрещин; на второй — объединение микротрещин и продвижение макротрещины на величину, сопоставимую с размером «процесс-зоны». Получены выражения для определения вероятностей образования микротрещин и продвижения фронта трещин при заданном характере нагружения.
Основные публикации:
- Чернякова Н. А.
Статистические оценки ресурса элементов конструкций на стадии роста усталостных трещин // Тр. III Всерос. конф. «Безопасность и живучесть технических систем». — Красноярск: ИВМ СО РАН. — 2009. — С. 271. - Чернякова Н. А.
Оценка ресурса элементов конструкций на стадии роста усталостных трещин // Материалы IV Междунар. конф. «Проблемы механики современных машин». — Улан-Удэ: ВСГТУ. — 2009. — Т. 3. — С. 243–244 . - Лепихин А. М., Чернякова Н. А., Москвичев Е. В.
Особенности расчета ресурса трубопроводов на стадии роста усталостных трещин // Тр. I научн-практ. конф. «Экспертиза промышленной безопасности опасных производственных объектов в условиях Крайнего Севера: проблемы и пути решения». — Якутск. — 2009. — С. 16-18.
| К началу | |